基于FPGA的自適應均衡器算法實現

摘要：近年來，自適應均衡技術在通信系統中的應用日益廣泛，利用自適應均衡技術在多徑環境中可以有效地提高數字接收機的性能。為了適應寬帶數字接收機的高速率特點，本文闡述了自適應均衡器的原理并對其進行改進。最后使用FPGA芯片和Verilog HDL設計實現了自適應均衡器并仿真驗證了新方法的有效性。

信道均衡技術(Channel equalization)是指為了提高衰落信道中的通信系統的傳輸性能而采取的一種抗衰落措施。它主要是減小信道的多徑時延帶來的碼間串擾(ISI)問題。其原理是對信道或整個傳輸系統特性進行補償，從而達到系統傳輸的要求。在實際的通信系統中，信道的特性是未知的并且是不理想的，傳統的均衡器無法滿足系統的要求，自適應均衡器直接從傳輸的信號中，根據某種算法不斷調整系統中濾波器的增益，來適應信道的隨機變化，從而有更好的失真補償性能，使均衡器總是保持最佳的工作狀態。FPGA以其處理速度快、開發周期短、可重復修改、開發工具智能、支持并行處理等優點成為現代通信領域硬件設計的首選方式之一。基于FPGA實現的自適應均衡器能夠更好地適應當前通信的發展要求，具有更廣闊的應用前景。

最小均方誤差算法(LMS)是較常用的一種實現自適應均衡器的算法，也是FPGA實現自適應均衡器的最理想的算法，所以本文選擇使用LMS算法設計均衡器。本文所設計的自適應均衡器是寬帶數字接收機的一部分，為了滿足寬帶系統的高速率，實時性的特點，在算法設計，對LMS算法進行一定的改進。

1 LMS算法基本原理

LMS算法是基于最小均方差準則的維納濾波器和最速下降法(method of steepest descent)提出的，其公式如下：

y(n)=uT(n)w(n) (1)

e(n)=d(n)-y(n) (2)

w(n+1)=w(n)+2μe(n)u(n) (3)

d(n)為期望輸入信號，e(n)為誤差，其中μ為步長因子，用以控制收斂速度與穩定性，LMS算法收斂的條件為：0

LMS算法的基本步驟如下：

步驟1，初始化w(0)=0，n=0;選擇μ;

步驟2，根據式(2)(3)計算誤差e(n)和w(n+1);

步驟3，若誤差不滿足要求，更新n=n+1，重復步驟2，若滿足要求則停止迭代。

下圖為最小均方誤差算法的原理框圖。

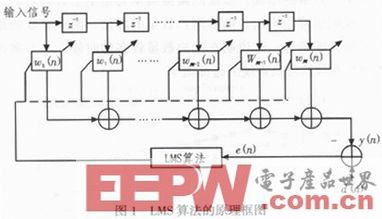
2 LMS算法改進

在寬帶系統中，數據量大，速率快，因此對均衡器的處理速度要求高，簽于此本文把變步長LMS算法和符號LMS算法結合在一起，以滿足上述要求。

步長因子μ控制著算法的收斂速度和穩定性，當μ較大時收斂速度快，穩定性較差，μ較小，穩定性好，收斂速度慢。變步長LMS算法可以兼顧收斂速度和穩定性兩個方面。一種變步長算法的公式為：

μ(n)=β[1-exp(-α|e(n)|2)] (4)

α、β為參數。由上式看到隨著誤差的減小，步長因子也在減小，穩定性增加。

公式(3)中，我們看到，每次迭代都會使用乘法器，運算量較大。符號LMS算法對公式(3)中的誤差e(n)進行縮放，每次迭代可減少使用一次乘法器，公式如下：

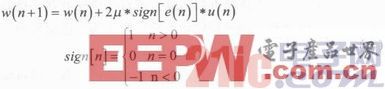
由公式(5)可以看出，符號LMS算法會損失一定的精度。變步長LMS算法可以改變步長以獲得快的收斂速度，結合符號LMS算法，可以大量減少運算量，提高系統的效率。本文對兩種算法的混合算法進行matlab仿真，選取64階均衡器，數據的訓練長度為1 000，跟蹤變步長計算的參數選擇α=4，β=1/128。下面對兩種方法混合算法用matlab仿真，并和傳統算法比較，如圖2所示。

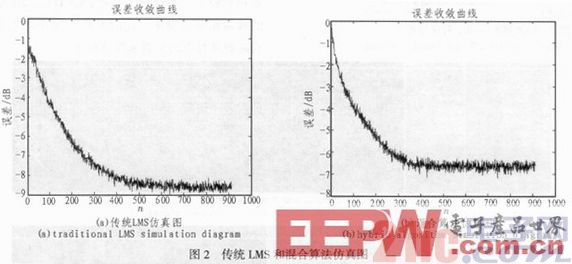
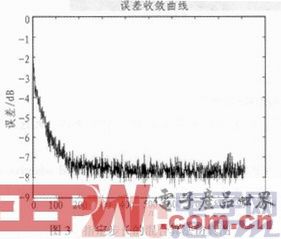
為了便于FPGA實現，按照變步長LMS算法思想，本文不在對變步長LMS算法中步長μ進行跟蹤計算，而是指定步長收斂之前為0.02，收斂之后步長0.15，其他參數不變，使用Matlab仿真，如圖3所示。

從圖中我們看到混合算法的誤差比傳統算法有所增大，但是在迭代300次后趨于穩定，比傳統算法減少200次，因此混合算法更能滿足實時性的要求。

圖3中，由于收斂之前步長且不隨誤差的減小而減小(迭代次數為200)，所以收斂速度更快;收斂之后步長較小，平均的穩態誤差比混合算法有所減小。

3 基于FPGA自適應均衡器的實現

由仿真可知，我們提出的混合算法可以滿足設計自適應均衡器的要求。本章將基于此算法的用FPGA實現自適應均衡器。

采用FPGA設計LMS自適應均衡器的結構圖如圖4所示。它主要分為FIR濾波器模塊、誤差計算模塊、權值更新模塊和狀態分配模塊4個單元。

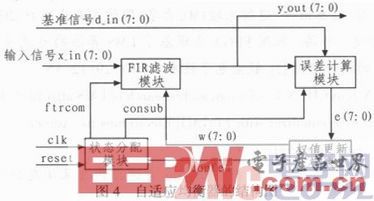
文中為了方便實現，FIR濾波器模塊實現18階的FIR濾波。誤差計算模塊中的基準信號d(k)事先可存在ROM里。權值更新部分實現FIR濾波器系數的計算與調整，設定收斂之前μ=2-4，收斂之后μ=2-6。

狀態分配模塊功能包括初始化各模塊，它產生控制信號、控制實現各個模塊完成特定功能;協調各個模塊間的操作。

由于FPGA不支持浮點數運算，而自適應濾波器必然要涉及到小數的計算，因此我們將所有小數化為二進制處理。本文設計采用4..4格式，第一位為符號位。

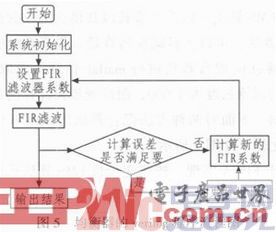
根據以上參數，按照LMS原理以及結構圖，我們即可編寫程序，主程序流程圖如圖5所示。