基于代數方法分析FIR濾波器

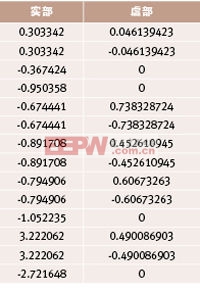
　　表1:等式中多項式的所有根[2]

　　共有 14 個根，因為是 14 級多項式（第 15 級是常數項，也就是 z 的零次方），其中 4 個是實數，其余為共軛復數。還記得求解二次方程的經典公式嗎？當平方根中的表達式為負時，就會形成根的虛數部分。正負號說明有兩個表達式，代表虛數不分彼此相反。

　　把所有項（z 的根）相乘，寫成因數形式。將復雜對結合為平方項，得出理想的實數系數，例如將共軛復數 x+jy 和 x-jy 相乘：

　　公式3

　　對表 1 中所有根或根對都采取這種算法（選擇實部相同的兩個根），我們得到等式 4:

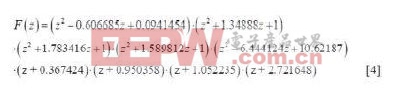
　　公式4

　　為了確保正確，我再次對等式[4]做乘法（利用 Excel），圖 2 說明我們返回了相同的濾波器。

　　順便說一句，可直接對脈沖響應使用 Excel 的 FFT 函數來獲得響應結果。如果手頭沒有仿真器，還可以使用另一種方法來計算頻率響應。濾波器在脈沖響應中只有 15 個有用的時間點，我用額外的零值將它擴展到 1024 點，得到一個具有理想頻率間隔的平滑 FFT 圖。

　　不過您可能會感到不解，做了這么多我們到底學到了什么？其實，有用的東西在于，因數的積代表濾波器行為。濾波器包括一系列連接塊，每個塊都被因數賦予一個多項式，從而形成小的濾波器。通過對 FIR 濾波器的大多項式因式分解，我們能獲得一系列小濾波器（每個具有 2 個或 3 個tap加權），串聯起來就能獲得與原濾波器相同的濾波器行為。

　　現在，IIR 濾波器通常被設計為二級串聯形式（即二次方程）。人們很少關心 FIR 濾波器的等效因式分解情況。這是因為 FIR 濾波器的實施已經很簡單了，因此細究也沒什么優勢。不過，在對 FIR 設計軟件得出的系數集進行分析時，這仍是很棒的工具。

　　我的主要目的并非是用這些工具拆分別人的 FIR 濾波器，而是用來發現因數本身的行為。我們隨后就能分別操縱每個因數，進而實現我們所需的功能。如果我們從頭創建某些因數，每個因數都能完成有用的功能，再將其組合在一起成為多項式，那么多項式系數也就是能夠同時完成所有功能的 FIR 濾波器的系數。

　　圖2:將等式[4]相乘所得多項式的響應情況

　　不妨考慮一下，我們的 FIR 濾波器在阻帶有三個空值（圖 1 和圖 2）。我們將多項式[4]進行因式分解后，有三個因數是常數項（即 z^0 的系數）。這并不是巧合。下次，我們要談談怎么驅動這一進程，讓因數滿足特定的阻帶行為。這將說明好的濾波器設計不止一個根！