遺傳模糊算法在短期負荷預測中的應用

提出了一種基于模糊邏輯原理的負荷預測方法，使用遺傳算法對系統參數進行訓練。在以往的模糊邏輯系統建立過程中,其主要參數（如模糊推理規則和隸屬函數等）需要依靠運行人員經驗或專家知識來確定，而本文利用遺傳算法，通過對樣本數據的自學習過程來獲取系統參數。在遺傳算法中，將推理規則與隸屬函數參數的確定結合在一起，從而確定系統參數的最優組合，由此建立起一個較合理的模糊負荷預測系統。仿真實驗結果表明，該方法能夠達到滿意的預測精度，具有良好的實用前景。
　　關鍵詞：短期負荷預測；模糊邏輯系統；遺傳算法

APPLICATION OF GENETIC-FUZZY ALGORITHM FOR SHORT TERM LOAD
FORECASTING OF POWER SYSTEM

Xiong Hao ；Luo Ri-cheng


(Electrical Engineering School ,Wuhan University, WuHan 430072, China)

　　ABSTRACT: A novel approach based on fuzzy logic system (FLS) is introduced to short term load forecasting (STLF).Traditional methods to choose membership functions and fuzzy control rules used to be done by means of integrating experience from experts in professional fields and technologic faculty. In this paper, however, a genetic algorithm based approach is developed to optimize parameters of membership functions and fuzzy control rules, simultaneously. And thus, the difficulties in building forecasting system, to some extent, can be disposed. At last, this new system is tested in an actual environment and produces superior results to traditional fuzzy logic short term load forecasting.
　　KEYWORDS: short term load forecasting; fuzzy logic system; genetic algorithm;


0 引言
　　 短期負荷預測是能量管理系統（EMS）的重要組成部分，也是確定機組組合、地區間功率輸送方案和負荷調度方案不可或缺的重要一環。由于負荷變化與許多因素有關，且各種因素之間相互牽連，很難確定每一種因素對預測值到底有多大的影響，因此，應用經典數學方法難以清楚地描述問題的內部機制，問題變得更加復雜。
　　 早期的負荷預測主要是運用回歸技術和時間序列法，但多為線性模型，不足以準確的描述電力系統負荷變化的非線性特性[1]。而近年來，人工神經網絡（ANN）運用于負荷預測的思想備受青睞。該算法具有很強的魯棒性、記憶能力、非線性映射能力以及強大的自學習能力，因而能夠迅速地擬和出負荷變化曲線。然而卻存在著收斂速度慢和容易陷入局部收斂等缺點，并且難以結合調度人員經驗中存在的模糊知識，而這一模糊知識卻又是極具價值的。
　　 模糊邏輯原理適合描述廣泛存在的不確定性，同時具有強大的非線性映射能力。已經證明模糊邏輯系統可以作為通用的模糊逼近器以任意精度逼近一個非線性函數,并且能夠從大量的數據中提取它們的相似性，這些特點正是進行短期負荷預測所需要的或是其他方法所欠缺的優勢所在[2]。上世紀九十年代初，國內外許多學者已經開始探索模糊邏輯原理在電力系統負荷預測中的運用[2][3][4]，某些機構還將這一理論運用于實際系統[5]。然而，在眾多的研究中，對于模糊推理規則和隸屬函數的選取仍然依賴于專家知識和運行人員的經驗，甚至在預測中需要運行人員參與其中[5]。這種建模方式需要工作人員對模糊系統的相關參數進行定期地離線修訂，系統建立耗時費力，且更新緩慢。本文結合模糊數學理論和短期負荷預測研究的最新成果，利用在求解組合優化問題中具有優良特性的遺傳算法來確定模糊邏輯系統的相關參數，從而較為迅速地構建出一套基于模糊邏輯原理的負荷預測系統。以期進一步挖掘模糊邏輯系統在負荷預測應用中的強大生命力。

1 遺傳算法在模糊邏輯系統中的應用
　　 一般來說，模糊邏輯系統的設計中最棘手的問題主要是以下兩個：其一為隸屬函數個數、形狀的確定及其坐標位置的調節；其二是模糊規則的確定，如果在推理句式已經固定的情況下，該問題又可細化為對各個模糊條件語句推理結果（后件模糊詞）的選取。兩部分內容互為依賴，相輔相成。已經有許多學者提出了許多有益的思想對這兩問題分別進行改進，然而由于隸屬函數與模糊規則具有高度的依賴性，最優模糊邏輯系統的建立取決于兩方面的有機結合，孤立地研究單方面因素的優化往往只能得出問題的次優解，難以在全局上把握問題的實質。事實上，隸屬函數參數的調節與模糊推理語句中待定模糊詞的選取可以看作是一個多參數組合優化問題。而遺傳算法非常適合于解決組合優化問題，它具有隱含的并行特性和全局搜索能力，可以很好地對隸屬函數和模糊規則進行綜合尋優。
　　設樣本集合的輸入量為X={x1,x2,…,xN},其中xj(j=1,2,…,N}為n維輸入向量，樣本集合的輸出量為Y={y1,y2,…,yN},樣本集合的輸入X對應的模糊邏輯系統的輸出為

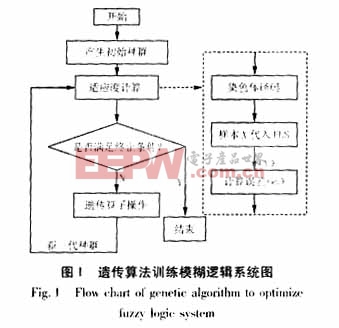
　　圖1表示了基于遺傳算法的模糊邏輯系統的訓練過程。設種群規模為K，每一次迭代所產生的染色體為lj(j=1,2,...K)。在適應度計算模塊中，首先對每次新產生得染色體lj進行解碼，還原成其所確定的模糊邏輯系統Lj。然后將樣本集合的輸入
集合的輸出量Y進行統計處理，抽取誤差平方和作為分析指標，即染色體lj對應的統計量作為其目標函數，如式（1）：
　
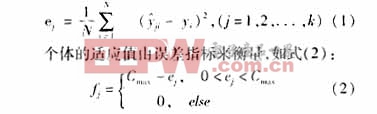
　　其中，Cmax為一給定值。選取f*為系統的最優適應值，當循環迭代出現期望的適應值fo(fo≥f*)時，迭代終止，由此確定最優模糊邏輯系統。

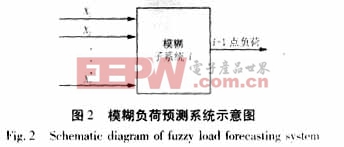
2 模糊負荷預測系統的參數選取
　　該系統的工作過程分為兩個階段：訓練階段和預測階段。訓練階段是將已知的歷史負荷資料作為評價指標，利用遺傳算法對模糊邏輯系統的參數進行選擇，這一階段可以看作是一個對人類經驗（備選解群）進行計算機總結進而尋找出最優模糊邏輯系統的過程。預測階段即系統的實際應用階段，將預測日的相關因素輸入預測系統，得出預測結果。
　　 本文設計的模糊負荷預測系統共分為24個獨立的小系統，每個小系統針對24個不同的時刻，對樣本數據分區處理。而在對預測日負荷進行集中預測。