基于卡爾曼濾波的電力系統短期負荷預測
2 卡爾曼濾波負荷預測模型
以連續若干天的同一時刻作為一組時間序列,來預測該時刻的下一個負荷值。通常,負荷值可以分為幾個部分:
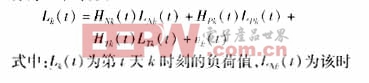
刻的基本負荷,Lpk(t)為前一天同時刻的的負荷值,LTk(t)為該時刻的氣溫,Vk(t)為誤差,HNk(t)、HPk(t)、HTk(t)均為參數矩陣。由于預測的是某個時刻的值,所以式中的各個量都是一維的。
為方便應用卡爾曼濾波理論進行狀態預測,特作如下變換:
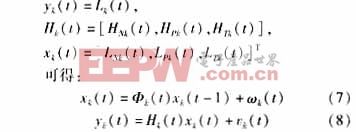
式中:yk(t)是觀測值,Hk(t)為觀測矩陣,Φk(t)為狀態轉移矩陣,Wk(t)為狀態誤差。由于在本文中狀態變量是連續若干天的同一時刻的溫度,它在短期的負荷預測中可以看成是緩變狀態,因此可令Φk(t)=I,I為單位陣。

2.1改進模型
在實際預測過程中,一般可以提供預測時刻的氣溫預報值,或者通過幾個點的預報值通過插值獲得其他點的氣溫值。本文提出了預測值修正方法,即在此預測值的基礎上加上溫度修正值的負荷預測方法。
設待預測的第(t+1)天時刻負荷的卡爾曼濾波預測值為yk(t+1|t),該時刻的狀態估計值為LTK(t+1|t),,而該預測時刻的氣溫預報值為Tk。狀態估計值是卡爾曼濾波器通過歷史負荷得到的對系統下一個時刻的狀態的最佳估計,而預報獲得的系統的新的狀態值則反映了系統的未來狀態,因此他們的組合能夠讓預測模型獲得更多的信息,從而得到更加準確的預測值。為利用此信息,可以對預測得到的值進行修正,即在[Tk-LTK(t+1|t)]前乘以一個修正系數,即:
式中:bk為修正系數,可以通過試驗獲得,yk(t+1)為該時刻修正后的負荷預測值。
3 短期負荷的預測實例
用卡爾曼濾波以及改進后的模型對武漢地區電力負荷進行預測實例計算。在實踐中初始狀態xk(0|0),Pk(0|0)很難準確掌握。但由于卡爾曼濾波在遞推過程中不斷用新的信息對狀態進行修正,所以當濾波時間充分長時,狀態初值xk(0|0)對xk(t+1|t)的影響將衰減至近于零,初始協方差陣Pk(0|0)對濾波估計協方差陣Pk(t+1|t)的影響也將衰減至于零。因此,濾波的初始條件可以近似確定。
每一次遞推運算中,要先求出預測值xk(t+1|t),然后根據預測值計算出預測誤差的方差Pk(t+1|t),由最佳濾波規則計算卡爾曼增益Kk(t+1),經過卡爾曼增益的誤差補償后獲得最佳濾波值xk(t+1),再由預測方程計算負荷預測值。
其中溫度參數在待預測天以前由歷史數據獲得,并對其進行濾波估計,而待預測天的溫度則由當天的溫度預報獲得。
引入誤差指標:
相對誤差:

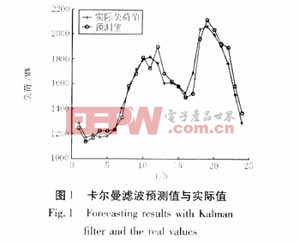
應用卡爾曼濾波模型以及改進后的模型對武漢地區的電力負荷進行實際預測,隨意抽取某一天的預測結果及誤差見下圖(1)、(2)、(3)、(4)。本文引用地址:http://www.104case.com/article/179691.htm






評論