基于開關電流技術的小波濾波器的實現
連續小波變換(Continuous Wavelet Transform,CWT)具有多分辨率的特點,可看成是帶通濾波器在不同尺度下對信號進行濾波。小波變換具有表征待分析信號在頻域上局部性質的能力,采用不同尺度a做處理時,各ψ(aω)的中心頻率和帶寬都不一樣,但品質因數卻不變,從頻域上看,用不同尺度做小波變換大致相當于用一組濾波器對信號進行處理。
開關電流電路是應用電流取樣表示信號的模擬電路,屬于電流模電路,具有電流模電路速度快、適于低壓工作,電流求和簡單等特點。另外,不需要線性浮置電容,適于CMOSVLSI工藝,并且在原理上,當用電流表示信號時,電壓擺幅不必大,具有低電源電壓工作潛力。
1 小波變換實現過程
連續小波變換的實現簡要概括為:根據母小波ψ(t)的頻域表達式。通過逼近得到母小波的有理式逼近形式,標準濾波器用來實現有理的和有限次傳輸函數,所以對信號的小波變換就轉換為將信號通過由母小波的有理式實現的濾波器來實現。該方法的實現取決于小波函數類型,這里以墨西哥小帽(Mexican Hat)小波為例,利用麥可勞林公式逼近得到能夠仿真實現的傳遞函數。
1.1 小波變換
設信號x(t)是平方可積函數,ψ(t)是被稱為基本小波或母小波的函數,則:
![]()
式(1)稱為x(t)的小波變換,其中a尺度因子,a>0,b反映位移,其值可正可負。
從定義上看,小波變換相當于信號x(t)與![]()
![]() 的卷積。眾所周知,一個濾波器電路的輸出是濾波器脈沖響應與輸入信號卷積,因此,實現對信號的連續小波變換CWT可以使信號通過濾波器實現。
的卷積。眾所周知,一個濾波器電路的輸出是濾波器脈沖響應與輸入信號卷積,因此,實現對信號的連續小波變換CWT可以使信號通過濾波器實現。
1.2 小波函數的逼近實現
這里以Mexican Hat小波(圖1)為例研究小波函數的實現方法,其時域表達式如式(2)所示:

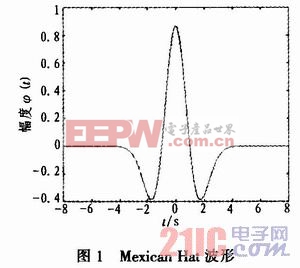
信號x(t)在尺度a下的CWT可通過轉移函數為H(jω)的濾波器來實現。然而,從圖1可以看出有兩個問題需要解決:1)ψ(t)是關于t=O對稱的,因此它是非因果的,任何濾波器的脈沖響應在右半平面有極點將會不穩定,為了能夠使其穩定,給一個時間延遲T;2)令S=jω,轉移函數轉換如式(4)所示。

式(4)中分母為指數形式,這樣傳輸函數就不能由只能實現有理的和有限次傳輸函數的標準濾波器實現。為了使傳輸函數有理化,通過使用麥克勞林公式近似逼近指數函數:
![]()
這樣就可以使要求的傳輸函數可以穩定的實現。通過近似得到的傳輸函數如式(6)所示:

為了實現小波設計過程,要選定合適的尺度a、時間延遲T和濾波器的階數,這些因素都是相關的。
基爾霍夫電流相關文章:基爾霍夫電流定律








評論