動力鋰電池離散特性分析與建模

　　3. 1 電池靜態離散模型

　　電池組的離散現象會隨著充放電循環次數的增多不斷惡化。在實際使用過程中， 電池組內單體容量的不一致和初始SOC 的不一致是電池組離散的主要原因。在經過若干次充放電循環后， 這些都會表現在電池組的SOC 離散特性中。

　　因此， 本文提出了一種基于電池荷電狀態的電池組離散度的概念， 以表征電池組具有一定離散度的特性， 并在數據統計和實際經驗的基礎上建立了基于電池荷電狀態的電池組離散度模型， 由整體離散度和極限離散度共同組成。式（ 3） 第一項描述的是電池組的整體離散度， 式（ 3） 第二項和第三項描述的是電池組的極限離散度。

　　式中， ε為電池組整體離散度； n 為電池組中電池單體數目； SOCi 表示電池單體的荷電狀態；

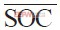
為電池組平均荷電狀態；ε p+為電池組正向極限離散度；ε p- 為電池組負向極限離散度； SOCmax 為電池單體荷電狀態極大值； SOCmin 為電池單體荷電狀態極小值。

　　式（ 3） 第1 項所描述的是電池組整體離散特性模型， 電池組的整體離散度是所有電池單體的荷電狀態的標準誤差， 反映了整組電池的離散態勢， 這一態勢不會因為個別單體電池的較大離散而劇烈變化。

　　而式（ 3） 中第2 項和第3 項所描述的是電池組極限離散特性模型， 電池組的極限離散度反映的是電池組中個別單體的荷電狀態與整組電池的平均荷電狀態相比， SOC 差異的極限離散態勢。正向極限離散度反映的是單體高于平均荷電狀態的極大值， 負向極限離散度反映的是單體低于平均荷電狀態的極小值。

　　（1） 開路電壓- SOC 模型

　　電池的開路電壓在數值上接近電動勢， 用開路電壓法可估計電池的SOC。

　　電池的開路電壓會受到電解液、溫度和SOC 的影響， 試驗用鋰離子電池單體不同溫度下的開路電壓曲線如圖5 所示。

　　由圖5 可以看出， 電池單體開路電壓受溫度的影響很小， 因此可以用多項式回歸的方法， 以SOC 為變量來描述電池單體開路電壓的變化。

　　令開路電壓y=Uoc, x=SOC, 多項式次數為7（ 多項式次數的確定是經過回歸分析、顯著性檢驗后得到） , 因此可將SOC 描述為開路電壓Uoc 的函數：

　　通過式（ 5） 可求得式（ 6） 中回歸系數的最小二乘估計， 于是， 得到開路電壓Uoc 與電池荷電狀態SOC的數學模型式（ 7） .

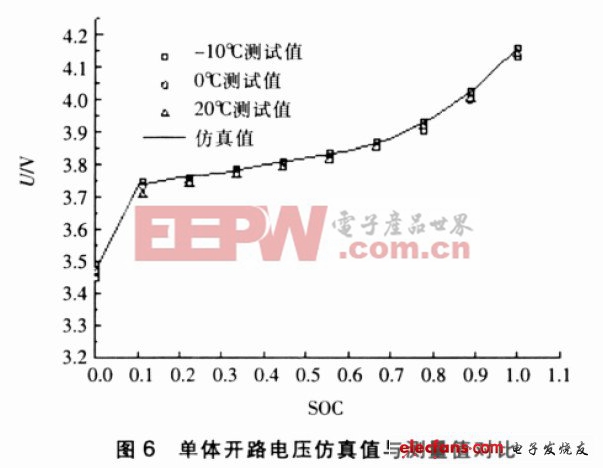
圖6 所示為電池開路電壓仿真曲線與實際值的比較， 結果表明： 以不同的方式達到一定的荷電狀態時， 電池的開路電壓基本符合SOC 與開路電壓的數學模型， 誤差在1%以內， 說明通過鋰離子電池的開路電壓估算其荷電狀態（ SOC） 是可行的。將式（ 3） 與式（ 4） 聯立， 可用電池開路電壓來描述電池組的離散度：

　　（2） 電池組靜態離散度模型的應用。

　　電池組靜態離散特性是由整體離散度和極限離散度聯合描述的。一方面給出了電池組當前離散狀態的量化指標， 并預測電池組的離散趨勢； 另一方面也為制定合理的電池管理控制策略和均衡充放電策略等提供依據。

　　圖7 所示是鋰離子電池組整體荷電狀態為0.75時的開路電壓分布情況。

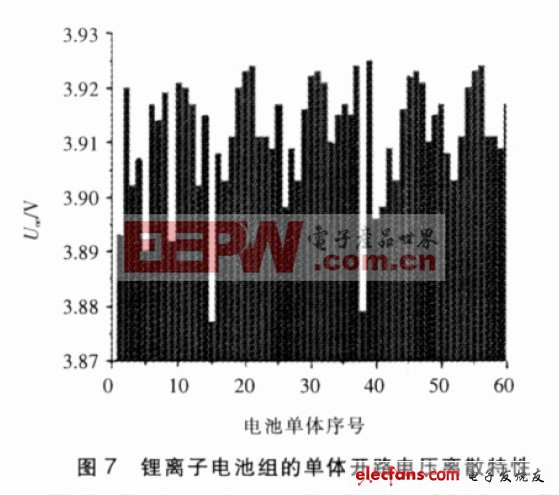
　　電池單體的平均電壓為3.9104V, 最高電壓為3.925V, 最低電壓為3.877V, 開路電壓標準偏差為0.01192V, 開路電壓極差為0.048V; 根據開路電壓與SOC 的函數關系可求得， 電池組平均SOC 為0.7493,最高SOC 為0.7711, 最低SOC 為0.6927, 整體離散度為1.89%, 電池組正向極限離散度為2.17%, 電池組負向極限離散度為5.66%.

　　電池組的整體離散度越大， 表示電池組整體離散愈嚴重， 更多的電池單體出現離散趨勢。大量試驗表明， 對于鋰離子電池組， 當整體離散度小于1%時，電池組一致性較好； 離散度介于1%- 3%, 電池組處于輕度離散； 離散度介于3%- 5%, 電池組處于中度離散； 當離散度高于10%時， 電池組處于重度離散，此時單體電池的性能嚴重不一致， 應考慮更換電池。

　　電池組的極限離散度越大， 則表明電池組中個別電池單體出現不一致的趨勢越大。正向極限離散度越大， 整組電池的充電接受能力越小； 負向極限離散度越大， 整組電池的放電能力越差。

　　根據上面的分析， 圖7 所示的電池組屬于輕度整體離散， 應考慮對單體15 號、單體38 號等進行更換或者補充電， 以提高該電池組的放電能力。