雙頻帶寬通帶毫米波濾波器設計

摘要：選取Y環和Y組成的復合圖形為基本圖形單元,采用密集三角形排布方式,設計了一種密集型組合單元頻率選擇表面(FSS)結構。基于譜域法,通過重新選取新的分析單元的方法,從理論上進行了頻譜分析。分析結果表明,該FSS結構能夠實現雙頻的寬通帶特性,并且具有很好的極化穩定性和角度穩定性。

1 引 言

由于周期結構可以控制電磁波的傳輸，近幾年周期結構的物理性質和應用得到了人們 的極大關注，比如頻率選擇表面(FSS)[1]和光子帶隙材料[2]。頻率選擇表面可以作為空間 濾波器，與電磁波相互作用表現出明顯的帶通或帶阻的濾波特性。它是由周期性排列的金 屬貼片單元或金屬屏上周期性的開孔單元構成的一種二維周期陣列結構。因其具有特定的 頻率選擇作用而廣泛地應用于微波[3]、紅外直至可見光波段[4]。

隨著對FSS 研究的深入，研究范圍也越來越廣，涉及到介質加載的FSS、非常規單元 FSS、非常規排列FSS、雙屏FSS 等[5]。如何實現FSS 的多通帶和寬頻帶的頻率響應特性也 成為研究的熱點[6]。

單元周期大小對FSS 的傳輸帶寬的影響很大[1]，因此我們可以通過調整單元之間的間 距來調整兩個通帶的帶寬。Y 環和Y 縫單元為FSS 結構中常用的單元[7]，本文通過將兩者 組合，以組成的復合圖形為基本圖形單元，并且采用密集型的單元排布方式，設計了一種 組合單元密集型FSS 結構。頻譜分析結果表明，此結構是一種同時具有雙頻和寬通帶特性 的毫米波濾波器，并且濾波特性對于不同的極化方式和不同的入射角度具有較好的穩定性。 這些特性在航天航空以及多頻段地面天線站衛星通訊領域有重要的應用[8]。因此，對這種 組合單元密集型FSS 傳輸特性的研究具有十分重要的理論意義和應用價值。

FSS 的理論分析方法很多，有 B.A.Munk 和R.J.Luebbers 等人的模式匹配法[9]、T.K.Wu 和R.Mittra 等人的譜域分析法[10]、E.A.Parker 和J.C.Vardaxoglou 等人的等效電路法[11] 等。本文采用譜域法對組合單元密集型FSS 結構進行分析。

2 理論分析

利用譜域法分析孔徑型FSS 結構電磁散射問題，第一步是把FSS 的散射場及入射場與屏 上的表面感應磁流建立聯系。自由空間的孔徑型FSS 分布在X-Y 平面，首先建立單個周期單 元的積分方程，然后修改為整個周期陣列的積分方程。

如圖1 所示為組合單元FSS 結構的單元排布方式，單元以Dy和Ds為周期進行排布，兩 個周期方向的夾角為θ ，此時每個單元的平均占有的面積為S，如表達式(1)所示。當單 元以傳統的松散結構排布時[13]，組合單元本身就可以作為周期單元進行計算;但是對于密集 型排布的FSS 結構，面積為S 的區域已經不能容納組合單元，因此，計算時組合單元不能作 為周期單元，只能選取新的周期單元。本文選取了如圖2 所示的新的周期單元，X 方向周期 為a，Y方向周期為b，見表達式(2)。

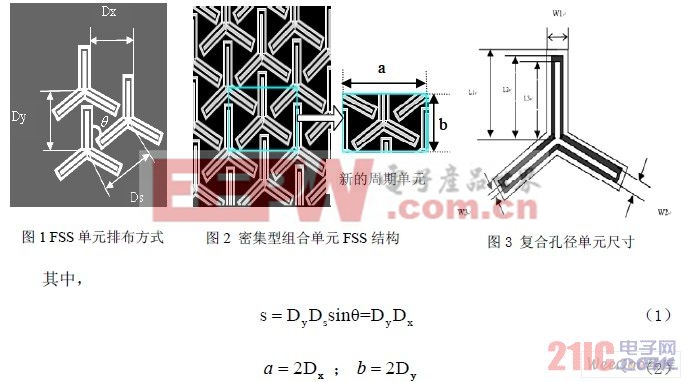
在x 方向和y 方向上的周期，θ 是FSS 兩個周期方向夾角，對于新選定周期單元θ =90°。 對于有介質加載的情況，只需將自由空間的格林函數換成有介質加載時的格林函數即可。 用矩量法求解方程(6)，基函數選用子域基函數中的Rooftop 函數[12]，就可以求出等效磁 流M ，進而可以求出反射和透射系數。