遺傳算法在PFC控制電路優(yōu)化設(shè)計(jì)中的應(yīng)用研究
3 遺傳算法控制參數(shù)優(yōu)化設(shè)計(jì)
為了使PFC電路有較好的穩(wěn)定性和動(dòng)態(tài)性能,必須對(duì)電流環(huán)和電壓環(huán)進(jìn)行反饋綜合,通過適當(dāng)?shù)难a(bǔ)償網(wǎng)絡(luò),合理配置零極點(diǎn),改善電路特性。
電流環(huán)反饋補(bǔ)償網(wǎng)絡(luò)采用如圖2所示的單零點(diǎn)雙極點(diǎn)網(wǎng)絡(luò)。
則電流環(huán)的開環(huán)傳遞函數(shù)為:
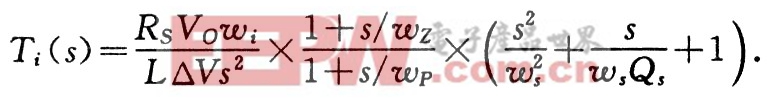
其中:RS為電流采樣電阻,VO為輸出電壓,![]() 為主電路電感,△V為PWM控制器三角波峰峰值,
為主電路電感,△V為PWM控制器三角波峰峰值,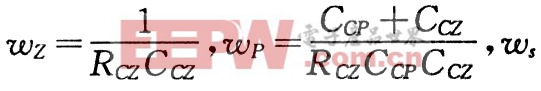 為切換頻率
為切換頻率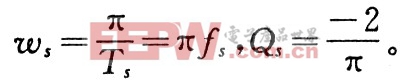 選擇設(shè)計(jì)變量為X=[x1,x2,x3,x4]=[RCI,CCP,RCZ,CCZ],則可求出電流環(huán)的開環(huán)傳遞函數(shù)與設(shè)計(jì)變量之間的關(guān)系式:
選擇設(shè)計(jì)變量為X=[x1,x2,x3,x4]=[RCI,CCP,RCZ,CCZ],則可求出電流環(huán)的開環(huán)傳遞函數(shù)與設(shè)計(jì)變量之間的關(guān)系式:
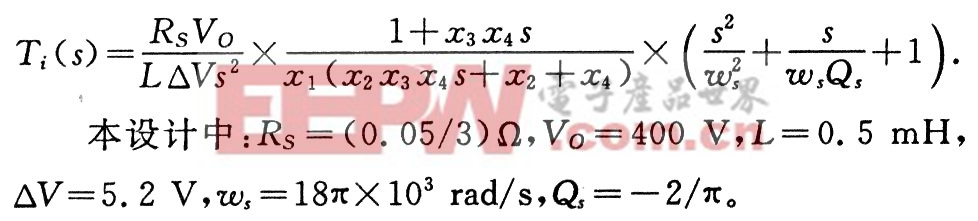
采用C語言編寫程序,并用SIMULINK進(jìn)行仿真。
待優(yōu)化控制參數(shù)為X=[x1,x2,x3,x4]=[RCI,CCP,RCZ,CCZ],屬于多參數(shù)優(yōu)化問題。將各參數(shù)分別用10位格雷碼表示,并將其首尾串聯(lián),形成40位的染色體串。初始種群X=[x1,x2,x3,x4]=[RCI,CCP,RCZ,CCZ]初始值以上一節(jié)初步設(shè)計(jì)各參量的取值X*為中心,在一定范圍內(nèi)向兩邊取值即X0=X*×(1士δ),取δ=0.3。
種群規(guī)模:N=31;最大迭代次數(shù):Gmax=400;每次遺傳操作后保留一個(gè)最優(yōu)個(gè)體;
遺傳算子系數(shù)取為:
a=0.6,b=0.2,c=0.2,d=0.19,即:PC=a+bT=0.6+0.2T,PM=c-dT=0.2-0.19T。
采用大變異策略PC,PM的變化范圍為0.6~0.8和0.01~0.2。
將系統(tǒng)在單位階躍函數(shù)下的![]() 、電流環(huán)傳遞函數(shù)TI(s)的開環(huán)穿越頻率WCI結(jié)合,分別取一定權(quán)值作為評(píng)價(jià)函數(shù),但因?yàn)檫z傳算法只針對(duì)最大值且不能為負(fù),所以適應(yīng)度函數(shù)取為其倒數(shù):
、電流環(huán)傳遞函數(shù)TI(s)的開環(huán)穿越頻率WCI結(jié)合,分別取一定權(quán)值作為評(píng)價(jià)函數(shù),但因?yàn)檫z傳算法只針對(duì)最大值且不能為負(fù),所以適應(yīng)度函數(shù)取為其倒數(shù):![]()
其中,k1、k2分別為兩個(gè)評(píng)價(jià)因子的權(quán),優(yōu)化過程中取為0.5。
因?yàn)椴捎眠B續(xù)參數(shù)編碼,而實(shí)際工程中元件參數(shù)是標(biāo)準(zhǔn)化參數(shù),在優(yōu)化過程中,采用動(dòng)態(tài)規(guī)劃思想進(jìn)行分部設(shè)計(jì)。即:
首先,對(duì)四個(gè)參數(shù)進(jìn)行編碼并優(yōu)化,將得出的最優(yōu)值與標(biāo)準(zhǔn)參數(shù)對(duì)比,選取最接近標(biāo)準(zhǔn)參數(shù)或由最多兩個(gè)標(biāo)準(zhǔn)元件串聯(lián)(或并聯(lián))能夠得到的一個(gè)參數(shù)值,將其確定。然后,對(duì)剩下的三個(gè)參數(shù)重新編碼、尋優(yōu)、確定第二個(gè)參數(shù)。以此類推,直至四個(gè)參數(shù)全部確定。
4 實(shí)驗(yàn)結(jié)果分析
我們應(yīng)用本文提出的改進(jìn)的遺傳算法(Modified Genet-ic Algorithms簡稱MGA)進(jìn)行了參數(shù)優(yōu)化,其結(jié)果和頻域初步設(shè)計(jì)結(jié)果對(duì)比及兩組參數(shù)下電流環(huán)暫態(tài)響應(yīng)性能指標(biāo)分別如表1、表2所示:
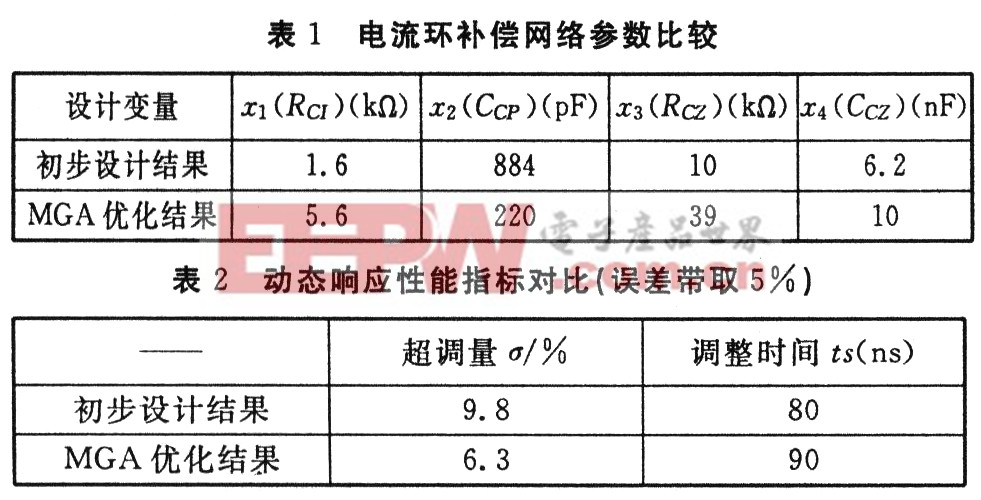
分別應(yīng)用兩組參數(shù)階越響應(yīng)進(jìn)行仿真,仿真結(jié)果比較如圖4:
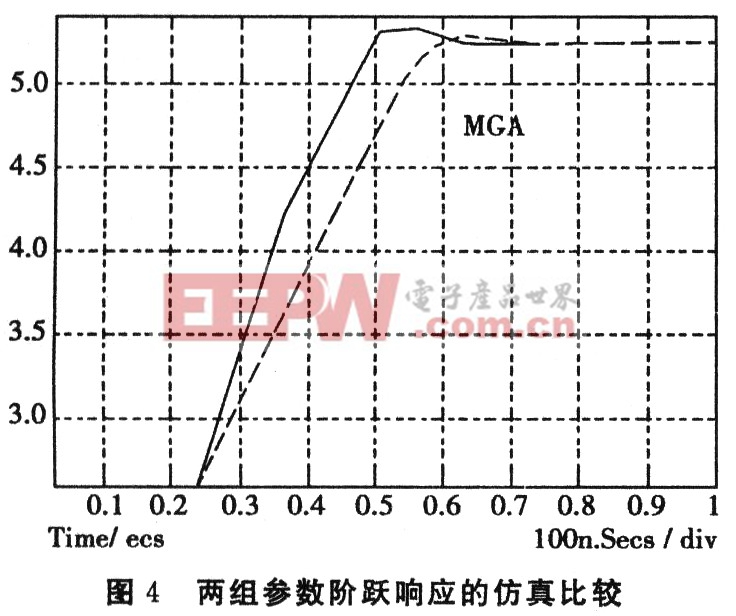
由圖4可以明顯地看出超調(diào)量減小,過渡時(shí)間縮短,控制系統(tǒng)的時(shí)域性能指標(biāo)有很大改善。仿真結(jié)果說明了優(yōu)化參數(shù)的有效性與優(yōu)越性。
DIY機(jī)械鍵盤相關(guān)社區(qū):機(jī)械鍵盤DIY








評(píng)論