單級倒立擺控制系統的穩定性算法設計
1 一級倒立擺系統的數學模型
本文引用地址:http://www.104case.com/article/162230.htm對于倒立擺系統來說,如果忽略了空氣阻力和各種摩擦之后,可將直線一級倒立擺系統抽象成沿著光滑導軌運動的小車和通過軸承連接的勻質擺桿組成,如圖1所示。其中,小車的質量M=1.32 kg,擺桿質量m=0.07 kg,擺桿質心到轉動軸心距離l=0.2 m,擺桿與垂直向下方向的夾角為θ,小車滑動摩擦系數,fc=0.1。
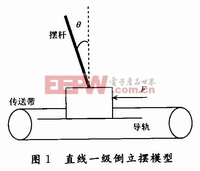
倒立擺控制系統數學模型的建立方法一般有利用牛頓力學的分析方法和分析力學中的拉格朗日方程建模兩種。本文采用的是拉格朗日方程建模。
一級倒立擺系統的拉格朗日方程應為:
式中:L是拉格朗日算子;V是系統動能;G是系統勢能。
式中:D是系統耗散能;fi為系統在第i個廣義坐標上的外力。
一級倒立擺系統的總動能為:

一級倒立擺系統有4個狀態變量,分別是
,根據式(7)寫出系統狀態方程,并在平衡點處進行線性化處理,得到系統的狀態空間模型如下:

2 倒立擺性能分析
系統的能控性是控制器設計的前提,所以在設計前對系統進行能控性分析,根據能控性矩陣T0=[B,AB,A2B,A3B],利用Matlab中的rank命令,可以得出rank(T0)=4。由此可知,系統是完全可控的,因此可以對系統進行控制器的設計,使系統穩定。
3 LQR控制器的設計
3.1 LQR控制器原理
線性二次型調節器的控制對象是線性系統,這個線性系統必須是狀態空間的形式,即:
,Y=Cx+Du。通過確定最佳控制量U*=R-1BTPX=-KX的矩陣K,使性能指標
的值極小。其中,加權矩陣Q和R是用來平衡狀態變量和輸入變量的權重;P是Riccati方程的解。這時求解Riccati代數方程:
就可獲得P值以及最優反饋增益矩陣K值:
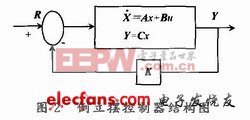
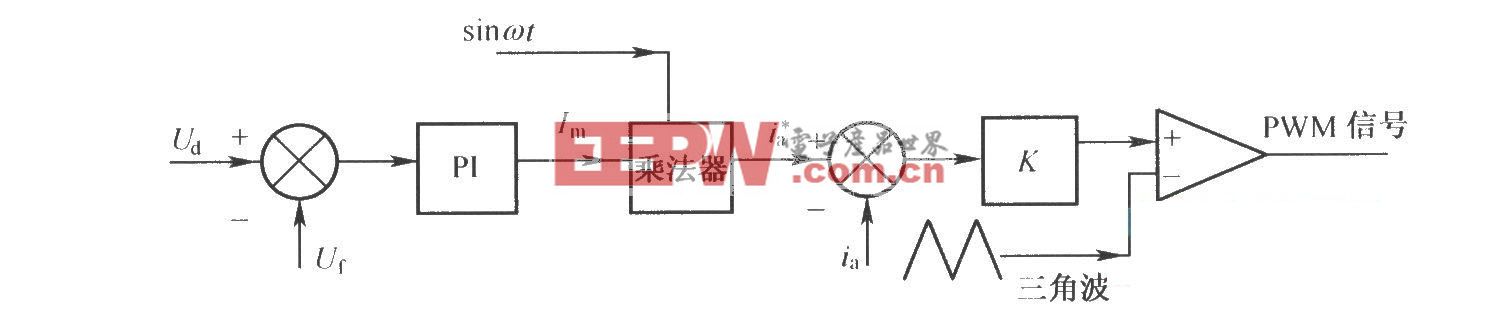
LQR用于單級擺的原理圖如圖2所示。









評論