評估電子元件老化和穩定性的高溫老化方法

了解由于使用石英晶體的溫度和時間，以及應用外推方法、老化方程和Arrhenius方程，電子元件的老化和穩定性挑戰。

即使有固定的輸入，電子電路也不是完全穩定的；經常隨時間和溫度漂移。這些與理想行為的偏差會給精確測量增加相當大的誤差。隨時間漂移，也稱為長期穩定性，是需要長時間高精度應用的關鍵因素。測量系統的初始精度誤差通常可以通過初始校準來消除；然而，消除長期漂移的誤差需要定期校準。此外，這些校準在某些工業、醫療、軍事和航空航天應用中可能不切實際。

在這篇文章中，我們將介紹評估電子元件長期穩定性的高溫加速老化方法的基礎知識。雖然我們將以典型石英晶體的老化行為為例，但類似的概念有時也適用于其他組件。

石英晶體老化機理——傳質效應

晶體的共振頻率隨時間而變化。石英晶體的兩種主要老化機制是傳質和應力釋放。當向晶體中添加或從晶體中去除少量質量時，諧振頻率會發生變化。為了盡量減少傳質效應引起的晶體老化，晶體的制造過程應盡可能清潔。

下圖1中，橙色曲線顯示了由于污染引起的傳質而隨時間漂移的晶體的典型老化行為。

一個顯示傳質引起的時間漂移的例子。

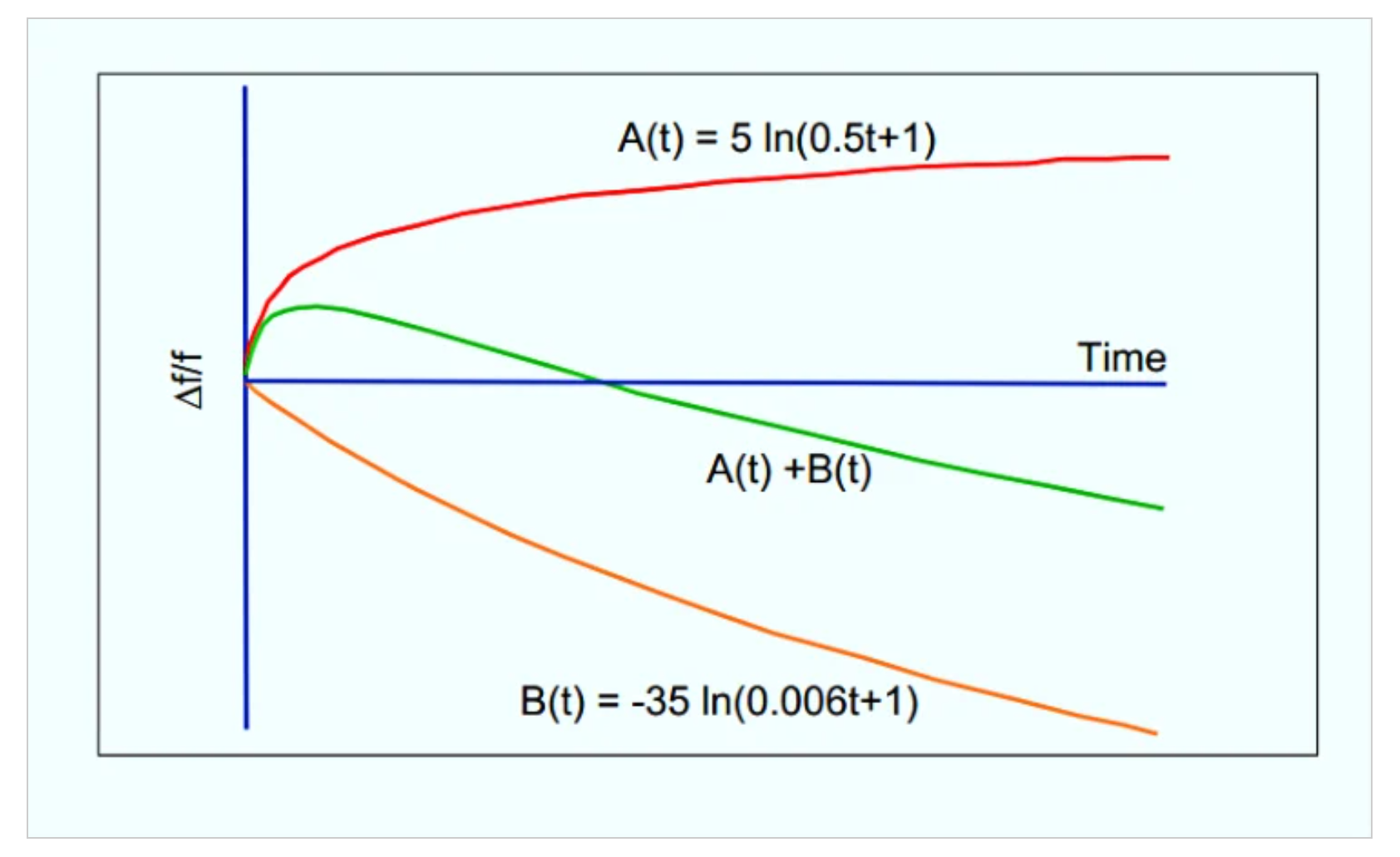
圖1。一個展示不同衰老因素和行為的例子。圖片由J.Vig提供

諧振頻率還取決于施加到晶體上的應力。這種應力可能是由PCB或封裝材料引起的。隨著時間的推移，這些應力會降低并導致晶體諧振頻率的變化。

圖1中的紅色曲線顯示了由應力釋放效應引起的典型老化行為。如果晶體的老化主要由傳質效應主導，其老化曲線將接近B（t）。對于受應力釋放效應影響的晶體，其老化行為將接近a（t）。總體老化行為（圖1中的綠色曲線）將是這兩條曲線的總和。

通過外推法進行老化預測

基于上述討論，我們可以使用以下對數函數來描述諧振頻率隨時間的變化：

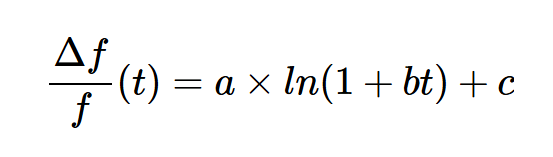
方程式1。

在這個方程中，a、b和c是常數，應該通過將模型與特定類型晶體的測量數據相關聯來獲得。這些常數可以通過應用最小二乘擬合過程來找到。圖2顯示了在室溫下從晶體收集的頻率漂移數據，以及通過將上述對數模型擬合到測量數據而獲得的曲線。

來自室溫晶體的頻率漂移數據集和使用對數模型的曲線。

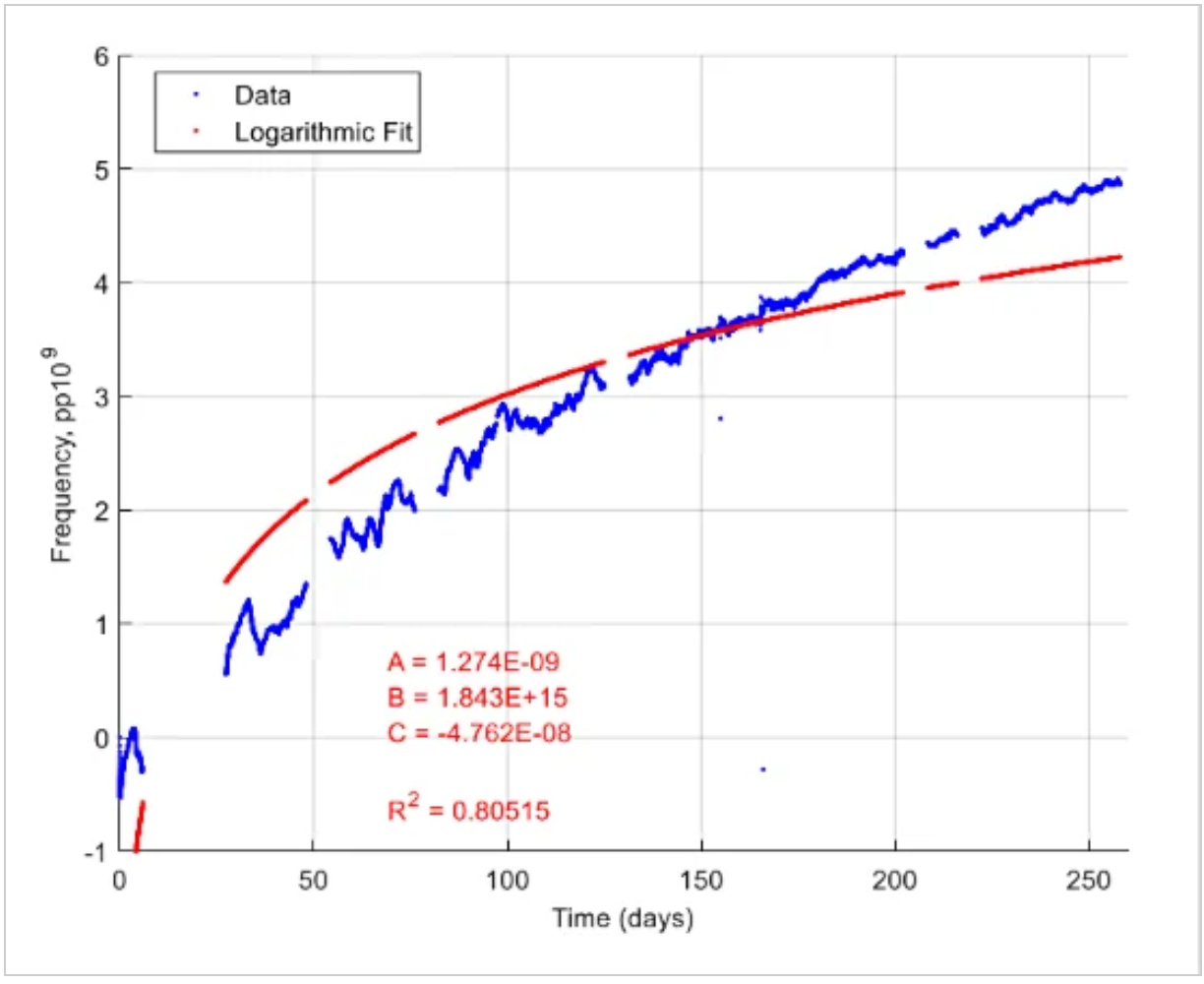
圖2:來自室溫晶體的頻率漂移數據集和使用對數模型的曲線。圖片由S.J.Griffin提供

有了模型參數，我們可以估計測試持續時間之外的頻率漂移。在示例文獻中，這種方法有時被稱為外推法。這種方法的缺點是它需要很長的測試時間。在上述示例中，捕獲約250天的頻率漂移數據以找到模型參數。在一篇名為“石英晶體單元的老化預測”的示例論文中，在室溫下測量了6個月（4320小時）的晶體諧振頻率，以便能夠準確確定一年后的頻率漂移。由于此類測試的成本過高，研究人員試圖找到更有效的衰老預測技術。為了更好地理解這些方法，我們需要更仔細地研究晶體的老化特性，我們稍后將對此進行介紹。

此外，值得一提的是，上述對數函數是一個相對簡單的模型，還有其他更復雜的模型可以更好地描述晶體的老化行為。

一個通用的石英晶體老化方程

由方程1給出的對數模型僅指定了老化過程的時間依賴性。石英晶體的一般老化方程可以寫成：

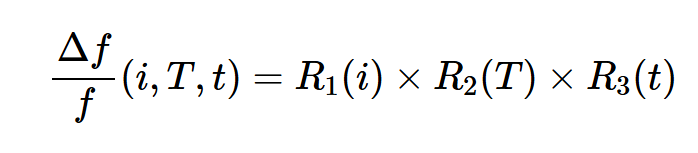
方程式2。

其中R1（i）、R2（T）和R3（T）分別考慮了對驅動水平、溫度和時間的依賴性。驅動電平是指晶體中消耗的功率量。超過規定的驅動器級別會縮短設備的壽命。在檢查老化效應時，選擇適當的驅動器級別以最小化由驅動器級別依賴性引起的頻率變化。忽略驅動器級別效應，方程式2可以寫成：

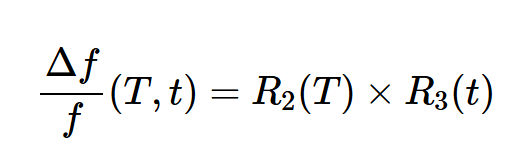
通過上述對數方程對老化過程的時間依賴性進行建模，我們得到：

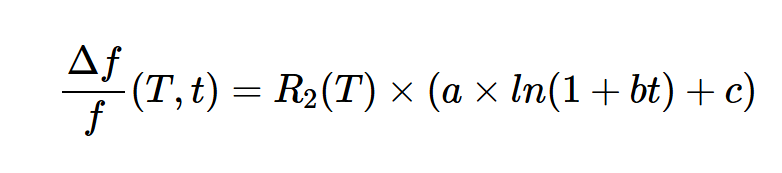
方程式3。

正如你從這個方程中看到的，為了對衰老過程有一個更準確的模型，我們需要確定衰老機制的溫度依賴性。這可以通過下面討論的Arrhenius定律來實現。

基于Arrhenius方程的溫度依賴模型

在物理化學中，Arrhenius方程是一個描述反應速率溫度依賴性的公式。根據Arrhenius方程，化學反應的速率常數對絕對溫度的依賴關系由下式給出：

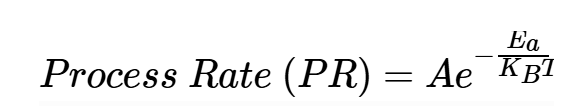
方程式4。

在上述方程式中：

Ea是反應的活化能（單位與KBT相同）

kB=8.617?10-5eV/K是玻爾茲曼常數

T是開爾文溫度

A是一個常數

根據該方程式，通過提高溫度（T）可以加速反應。當應用于老化預測問題時，Ea是老化過程的活化能。應該指出的是，并非所有的衰老機制都遵循Arrhenius定律。

假設感興趣晶體的老化遵循Arrhenius方程，方程3可以表示為：

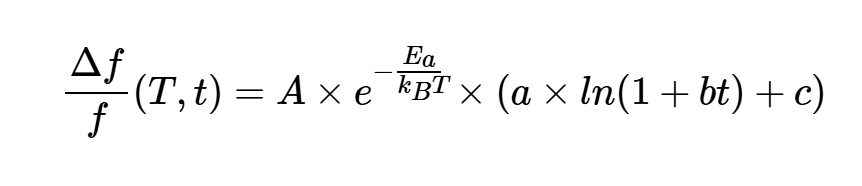
在某些假設下，上述方程可以簡化為：

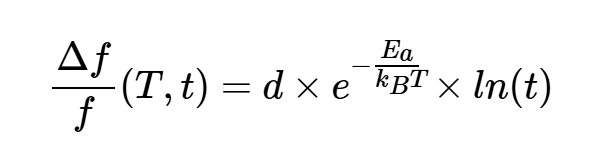
方程式5。

其中d是常數。

高溫加速老化

方程式5解釋了老化過程如何隨時間和溫度變化。由于老化過程在高溫下加速，我們可以將晶體在高溫Ttest下浸泡相對較短的時間，以預測在正常工作溫度Tuse下更長時間的老化效果。

從方程式5中，我們得到：

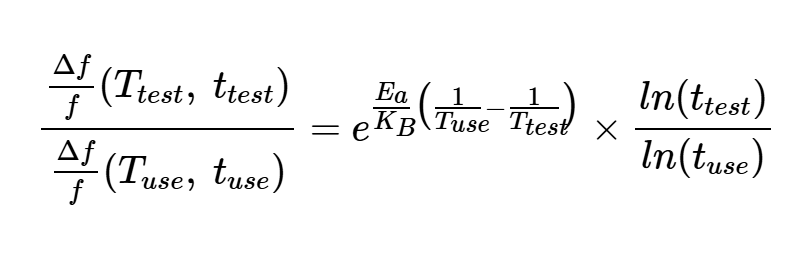
例如，Ea=0.2eV，Ttest=85°C，Ttest=7天，Tuse=25°C，Tuse=365天；上述比率等于約2。這意味著，在Ttest=85°C的溫度下，晶體在Ttest=7天內的老化時間大約是Tuse=25°C的晶體在Tuse=365天內老化時間的兩倍。因此，為了估計在25°C下一年后的晶體老化，我們可以測量在85°C下浸泡7天的晶體的老化。將該值除以2，我們可以得到一年后在25°C下的晶體老化。

要應用上述方法，我們需要知道老化過程的活化能。這將在本系列的下一篇文章中討論。應該指出的是，Arrhenius方程有一些局限性。事實上，你可以在研究論文和制造商的技術文件中找到關于這種方法的相互矛盾的意見。在下一篇文章中，我們也將探討其中一些相互矛盾的觀點。