直流傳感器回饋補(bǔ)償系統(tǒng)設(shè)計(jì)

　　PID運(yùn)算電路的工作過程如下：當(dāng)輸入信號(hào)Ii有一階躍變化時(shí)，一開始CD、C1，相當(dāng)于短路，輸入信號(hào)突跳至微分作用最大值。繼而隨著對(duì)CD的充電，負(fù)反饋電壓逐漸升高，輸出電流I0逐漸衰減下來(lái)。與此同時(shí)，CI也被充電，隨著CI兩端電壓逐漸增加，負(fù)反饋?zhàn)饔弥饾u減小，輸出電流I0又慢慢上升。在Ii階躍作用下，PID輸出特性曲線見圖5。

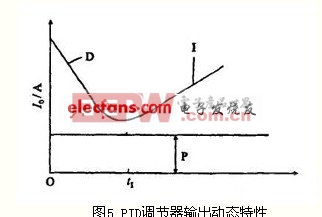
　　PID控制器的傳遞函數(shù)可表示為：G2(s)=KP(1+1/stI)(1+stD)

　　式中，比例作用KP=R2/R1=10，積分作用t1=R2C2，微分作用tD=R1C1。

　　2.1.3 反饋繞組傳遞函數(shù)

　　反饋繞組的傳遞函數(shù)用G3表示：G3=1/(Ls+R)=L=2.7418H

　　式中：R=25Ω，為反饋繞組回路總電阻;μ為鐵心導(dǎo)磁率，H/m;A為鐵心截面積，O;l為鐵心平均磁路長(zhǎng)度，m;L=2.7418H，為反饋繞組的自感;從為反饋繞組匝數(shù)。

　　阻抗增益：G4=1/R=0.06，反饋繞組的比例系數(shù)：G5=2000。

　　3 差值電流回饋補(bǔ)償系統(tǒng)的德定性分析

　　差值電流回饋補(bǔ)償系統(tǒng)的開環(huán)傳遞函數(shù)為：

　　閉環(huán)傳遞函數(shù)的特征方程為：

　　D(s)=sti(s+9.1)+264(1+st1)+(1+stD) =(264tDt1+t1)s2+(264(tD+t1)+9.1t1)s+264

　　差值電流回饋補(bǔ)償系統(tǒng)是一個(gè)典型的閉環(huán)系統(tǒng)。根據(jù)李雅普諾夫穩(wěn)定性理論，線性系統(tǒng)穩(wěn)定的充分必要條件是閉環(huán)系統(tǒng)特征方程的根都具有負(fù)實(shí)部，即閉環(huán)傳遞函數(shù)的極點(diǎn)均位于坐標(biāo)平面左半部(不包括虛軸)。但當(dāng)系統(tǒng)階次較高時(shí)，在一般情況下，求解其特征方程會(huì)遇到較大的困難。勞斯及古爾維茨穩(wěn)定判據(jù)，可通過特征方程的根與各項(xiàng)系數(shù)的關(guān)系來(lái)判別系統(tǒng)的特征根是否全部具有負(fù)實(shí)部，從而分析線性系統(tǒng)的穩(wěn)定性。

　　古爾維茨穩(wěn)定判據(jù)求得系統(tǒng)穩(wěn)定的充要條件：264tDt1+t1>0且264(tD+t1)+9.1t1>0，可見，只要tD>0，t1>0，系統(tǒng)就是穩(wěn)定的。

　　4 結(jié) 語(yǔ)

　　磁勢(shì)自平衡回饋補(bǔ)償式直流傳感器的磁勢(shì)平衡由鐵心的近似矩形磁化曲線決定。其差值電流補(bǔ)償電路，則是利用雙向鐵心磁放大器的基本原理，在電抗器鐵心的空腔內(nèi)設(shè)置零安匝檢測(cè)鐵心和線圈，用以檢測(cè)該半周期內(nèi)直流磁勢(shì)平衡的安匝差以自動(dòng)跟蹤補(bǔ)償。根據(jù)勞斯陣列的第一列元素符號(hào)均為正值可判斷差值回饋補(bǔ)償系統(tǒng)是穩(wěn)定的。