基于Taylor展開法整定MIC-PID控制器參數
加入技術交流群
3 控制過程仿真
設被控過程對象模型為：
，這里取ε=2，按式(27)、(28)、(29)整定PID參數，得K=0．344 75，Ti=3.331，TD=0．399 9；當取ε=4時，得K=0．218 3，Ti=3．164 3，TD=0．263 1。當取ε=6時，得K=0．159 4．Ti=3．081，TD=0．195 9。取α=0．05，其響應曲線如圖3所示。設被控過程對象模型為：
，這里取ε=1，按式(27)、(28)、(29)整定PID參數，得K=0．725 5Ti=1．982 2，TD=0．208；當取ε=2時，得K=0．463 4，Ti=1．898 9，TD=0．137 4其響應曲線如圖4所示。本文引用地址：http://www.104case.com/article/160269.htm
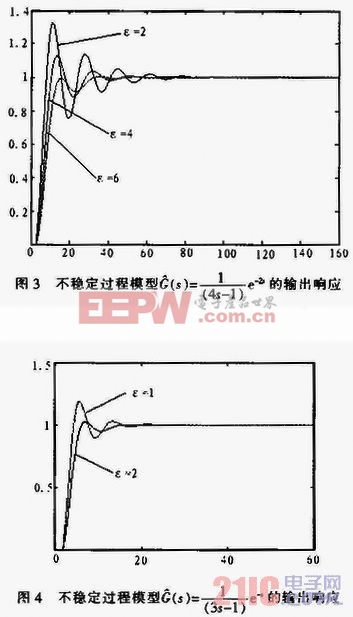
由圖3和圖4可見，如果純滯后時間變小有利于系統穩定，純滯后時間變大則系統容易發散，因此在整定參數時，可以人為地將延遲時間加大，以防止參數攝動時，系統不穩定。
4 結論
文中采用內模控制原理，針對一類不穩定時滯過程，采用雙環控制結構，首先使廣義對象(內環)穩定，然后按內模控制原理設計外環控制器，利用Taylor級數展開法得到了PID參數整定公式。通過仿真實例對IMC-PID控制器進行驗證，結果表明在IMC-PID控制器的作用下被控系統不但具有良好的魯棒性，而且調節快速，便于實際系統應用。
pid控制器相關文章:pid控制器原理
評論