基于Taylor展開法整定MIC-PID控制器參數

摘要：針對一類不穩定時滯過程，采用雙環控制結構，首先使廣義對象(內環)穩定，然后用Tavlor級數展開法，根據內模控制原理設計外環控制器，得到等效的PID控制器參數的整定方法。仿真結果表明，整定后的系統不但具有良好魯棒性，而且調節快速，適合于工程實際應用。
關鍵詞：不穩定；Taylor展開；內模控制；PID控制；魯棒性

PID控制是迄今為止最通用的控制方法，它具有結構簡單，對模型誤差具有魯棒性和易于操作等特點，仍被廣泛應用于冶金、化工、電力、輕工和機械等工業過程控制中。在現有的PID參數整定方法中，Ziegler-Nichols法(簡Z-N法)應用最為廣泛。
內模控制(IMC)是一種實用性很強的控制方法，其設計簡單，跟蹤調節性能好，特別是對于魯棒性及抗干擾性的改善和大時滯系統的控制，效果尤為顯著。經過多年的發展，IMC方法的應用已經從線性系統擴展到了非線性和多變量系統，并產生了多種設計方法，如零一極點對消法，預測控制法，針對PID控制器設計的方法等。將IMC引入PID控制器的設計，既可以得到明確的解析結果，降低參數設計的復雜性和隨機性，又能方便地考慮到系統魯棒性的要求。本文針對一階不穩定時滯過程，通過對過程控制系統含有純滯后環節的近似處理，介紹了Taylor級數在MIC-PID參數整定中的應用，最后利用仿真進行了驗證。

1 內模控制
1)內模控制原理
內模控制器與簡單反饋控制結構的關系，可以用圖1來表示。

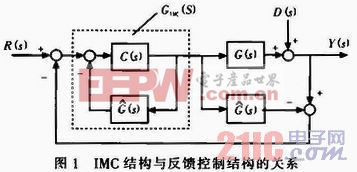
圖中C(s)為反饋控制器，GIMC(s)為內模控制器，為被控過程對象，G(s)為過程對象模型，R(s)為設定值輸入，D(s)為擾動輸入，Y(s)為系統輸出值。對于圖1中的內模控制器，有：

2)內模控制器的設計步驟