三維矢量散射積分方程中奇異性的分析及求解方法介紹
上式就是電場積分方程的主值積分.不難看出式(1)和(11)的區別僅為:主值積分的積分域不含有奇點,因此可用經典函數論的方法分析其積分值收斂趨勢.于是,阻抗元素計算式(4)可改寫為:本文引用地址:http://www.104case.com/article/153957.htm
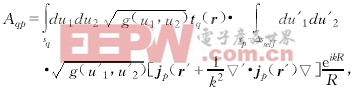
其中r∈sq,Δsself∈{Δs},∑Δs=sq,Δsself![]() sself=sq∩sp,Δsself→0 (12)
sself=sq∩sp,Δsself→0 (12)
由式(12)可知,在關于場點和源點的面積分中,被積函數包含了兩項:
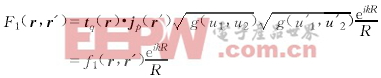 (13)
(13)![]() (14)
(14)
阻抗矩陣計算式(4)和(12)可分別簡寫為:
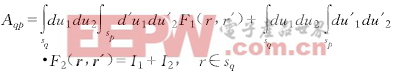 (15)
(15)
和
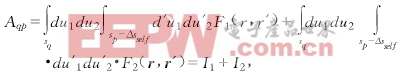 (16)
(16)
其中r∈sq,Δsself∈{Δs},∑Δs=sq,Δsself![]() sself=sq∩sp,Δsslef→0.
sself=sq∩sp,Δsslef→0.
式(15),(16)都能用來求解矩陣自阻抗元素.但式(16)對源點使用主值積分,便于數值分析.兩式中,I1=I′1,I2=I′2.為方便計,選擇其中的I1和I′2.
三、奇異項轉移方法
在式(13)中,僅包含弱奇異性的Abel積分核[7].一般來講,對于這類積分,數值計算時只要分格越細(不取奇點),所得的數值結果就越精確.但計算量增加.若取較少的節點,則由于被積函數在奇點附近變化劇烈,導致誤差增大.所以必須尋找一種在數值計算上實際可行的方案.處理這類奇異積分的方法之一是奇異轉移法[1].本文將這種方法進行了推廣,以便解決式(13)那樣的奇異問題.經過簡單的數學處理,得:
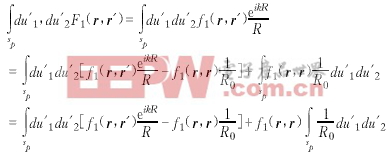 (17)
(17)
在上式中,第一項被積函數在積分域是連續有限的,因此數值可積.在第二項積分中,因子f1(r,r)只與場點有關,故可提到積分號外,因此簡化了奇異項以便于使用積分的解析解:
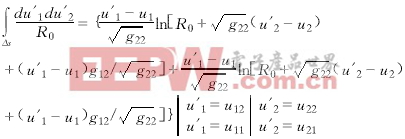
式中R0=![]() (19)
(19)
四、挖除有限小塊法
下面討論I′2的數值積分.積分項I′2不包含奇點,其被積函數F2(r,r′)在積分域上是解析的.但在奇點r附近,由于F2(r,r′)隨r′的變化非常劇烈,用一般的數值求積是很困難的.
用一有限小曲面塊ΔS包圍奇點(ΔS![]() sp),并設F2(r,r′)的陡變部分在ΔS中.取Δs0=ΔS-Δsself.在實際空間中,Δs0對應于一很小的曲面塊,即Δs01.而在參數空間中,Δs0則為一很小的矩形塊,其長為Δu1,寬為Δu2,如圖1.這時I′2變為:
sp),并設F2(r,r′)的陡變部分在ΔS中.取Δs0=ΔS-Δsself.在實際空間中,Δs0對應于一很小的曲面塊,即Δs01.而在參數空間中,Δs0則為一很小的矩形塊,其長為Δu1,寬為Δu2,如圖1.這時I′2變為:
 (20)
(20)
式中第一項不含陡變部分,所以可用一般的數值求積方法計算.第二項不含奇點,可以得到解析結果.
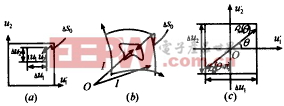
圖1 挖除有很小塊Δs0.(a)參數空間對應的矩形有限小塊,矩形中點為奇異點(u1,u2);(b)實空間對應的有限小塊Δs0;(c)參數空間中,奇異點(u1,u2)平移到原點0后,矩形有限小塊的極坐標圖 由式(14)可知,由于含有隨源空間r′變化的幾何因子
在上式中,A(r)為不隨源點變化的因子,而且
當Δs01,有R0≈R.
其中,
把式(26),(27)代入式(28),化簡后得I22=0.于是式(20)變成:I′2=I21+0=I21.從上述分析可知,分離的小塊域對積分無貢獻.所以,在實際計算中,可以方便地使用數值求積方法計算I′2,并令場點等于源點時的積分為零. |


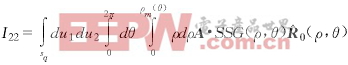 (28)
(28)





評論