基于TMS320LF2407的FFT算法的實現

1 快速傅里葉變換的原理

　　非周期性連續時間信號x(t)的傅里葉變換可以表示為

　　式中計算出來的是信號x(t)的連續頻譜。但是，在實際的控制系統中能夠得到的是連續信號x(t)的離散采樣值x(nT)。因此需要利用離散信號x(nT)來計算信號x(t)的頻譜。

　　有限長離散信號x(n)，n=0，1，…，N-1的DFT定義為：

　　可以看出，DFT需要計算大約N2次乘法和N2次加法。當N較大時，這個計算量是很大的。利用WN的對稱性和周期性，將N點DFT分解為兩個N/2點的 DFT，這樣兩個N/2點DFT總的計算量只是原來的一半，即(N/2)2+(N/2)2=N2/2，這樣可以繼續分解下去，將N/2再分解為N/4點 DFT等。對于N=2m 點的DFT都可以分解為2點的DFT，這樣其計算量可以減少為(N/2)log2N次乘法和Nlog2N次加法。圖1為FFT與DFT-所需運算量與計算點數的關系曲線。由圖可以明顯看出FFT算法的優越性。

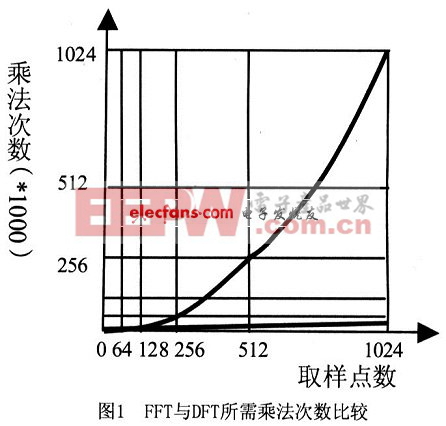
　　將x(n)分解為偶數與奇數的兩個序列之和，即

　　x1(n)和x2(n)的長度都是N/2，x1(n)是偶數序列，x2(n)是奇數序列，則

　　其中X1(k)和X2(k)分別為x1(n)和x2(n)的N/2點DFT。由于X1(k)和X2(k)均以N/2為周期，且WN k+N/2=-WN k，所以X(k)又可表示為：

　　上式的運算可以用圖2表示，根據其形狀稱之為蝶形運算。依此類推，經過m-1次分解，最后將N點DFT分解為N/2個兩點DFT。圖3為8點FFT的分解流程。

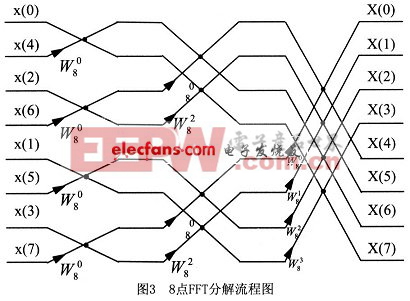
　　FFT算法的原理是通過許多小的更加容易進行的變換去實現大規模的變換，降低了運算要求，提高了與運算速度。FFT不是DFT的近似運算，它們完全是等效的。