分數階Fourier變換應用于水聲通信及其FPGA實現

　　傳統4FSK參數如下：載波頻率分別為f₁=4500Hz，f₂=5500Hz，f₃=6500Hz，f₄=7500Hz。

　　改進型算法參數如下：帶寬1.0kHz，脈寬0.02s，信號中心頻率分別為4.5kHz、5.5kHz、6.5kHz和7.5kHz，采樣頻率為48kHz。通過大數統計得到其誤碼率曲線如圖3所示。　　

?

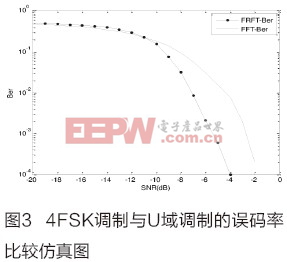　　由圖3可以知：當信噪比大于-11dB之后，4FSK調制解調方式誤碼率變化相對緩慢，而基于FRFT的u域調制解調方法誤碼率顯著下降。在信噪比為-4dB時，后者的誤碼率接近于零。

　　基于Ozaktas采樣型算法DFRFT的FPGA實現

　　基于FPGA硬件平臺的改進型Ozaktas采樣型算法實現流程主要分為以下兩個功能模塊：復數乘法器模塊、卷積處理模塊，其總體流程圖如圖4所示。　　

?

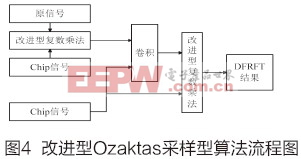　　離散分數階Fourier變換(DFRFT)計算需經過兩次復數乘法運算和一次與Chirp信號的卷積運算來得到DFRFT的結果。計算結果通過峰值位置搜索判決找到其峰值點進而判斷出其相對應的調頻率和中心頻率。

　　為了便于硬件的實現，減少FPGA的資源消耗，本文對復數乘法的實現進行了改進，下面具體介紹主要模塊的實現過程。

　　改進復數乘法器模塊

　　由圖4可知本算法的實現需要兩次復數乘法運算環節，因此對復數乘法的改進可提高運算效率。一般執行一次復數乘法需要4個乘法器和2個加法和減法器。本文通過代數方法重新推導公式，將復數乘法表達式重新寫成另外一種只需3個乘法器、3個加法器和2個減法器的表達式。設A=Ar+jAi，B=Br+jBi是兩個復數，那么復數乘法的標準表達式如下：

　　R=A×B=(Ar+jAi)×(Br+jBi)=Rr+jRi (3)

　　其中Rr=Ar×Br-Ai×Bi，Ri=Ar×Bi+Ai×Br，上述標準表達式需要使用4個乘法器。通過代數方法重新推導整理為：

　　Rr=Ar×Br-Ai×Bi (4)
　　Rr=Ar×Br-Ai×Bi+0 (5)
　　Rr=Ar×Br-Ai×Bi+(Ar×Bi-Ai×Br)-(Ar×Bi-Ai×Br) (6)
　　Rr=(Ar×Br-Ar×Bi+Ai×Br-Ai×Bi)+(Ar×Bi-Ai×Br) (7)