分數階Fourier變換應用于水聲通信及其FPGA實現
——
加入技術交流群
FRFT在信號處理和通信等領域已有許多應用[10]。本文利用FRFT適用于處理Chirp類信號的優勢，初步研究了基于FRFT的調制解調技術。
根據FRFT的逆變換公式：
???????? 
?
可知，信號x(t)的FRFT 可以理解為x(t)在以其逆變換核
為基的函數空間上的展開，而此核是u域上的一組正交Chirp基。因此一個Chirp信號在適當的u域中對于特定的Chirp信號具有最好的能量聚集特性。用FRFT實現線性調頻信號的參數檢測和估計可通過旋轉角α對變量進行掃描，通過對信號進行快速的FRFT，再以(α，u)的二維平面中進行峰值搜索，即可較準確估計被檢測信號的幅度、初始相位、起始頻率等參數值。?
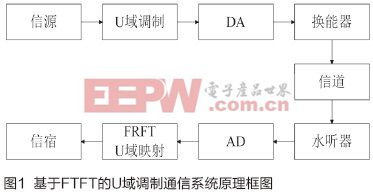
對于一組調頻斜率相同但中心頻率不同的線性調頻信號，可以根據不同的沖擊函數找到對應的原信號的頻率，從而還原出原信息。例如可將數字信息(00，01，10，11)調制到四組斜率相同但中心頻率不同的線性調頻信號上。在接收端將接收數據進行FRFT，之后將變換后的數據在u域進行峰值位置搜索，找到其最大值進而確定出原線性調頻信號的中心頻率，從而還原出原信息，上述過程如圖1所示。
?FRFT是線性變換，由于它具有信號能量聚焦性，而噪聲卻不會聚焦，使其在具有加性噪聲的多分量情況下更具優勢。為了更好地說明它的優點，進行了計算機對比仿真研究。
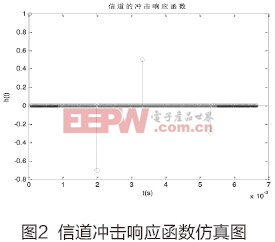
仿真條件：信噪比從-20dB至10dB，仿真信道如圖2所示?！ ?/p>
?
fpga相關文章:fpga是什么
數字通信相關文章:數字通信原理
通信相關文章:通信原理
評論