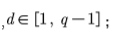SM2算法第三篇：實現SM2秘鑰交換協議的算法流程

參考文獻：SM2橢圓曲線公鑰密碼算法-第三部分（秘鑰協商協議）

一、概述

本部分規定了SM2橢圓曲線公鑰密碼算法的密鑰交換協議，并給出了密鑰交換與驗證示例及相應的流程。本部分適用于商用密碼 應用中的密鑰交換，可滿足通信雙方經過兩次或可選三次信息傳遞過程，計算獲取一個由雙方共同決定的共享秘密密鑰（會話密鑰）。同時，本部分還可為安全產品生產商提供產品和技術的標準定位以及標準化的參考，提高安全產品的可信性和互操作性。

二、術語和定義

1、密鑰  key

確定密碼參數運算的一個參數，它用于：

（a）加密和解密變換；

（b）同步產生共享秘鑰；

（c）數字簽名的生成和驗證。

2、密鑰交換  key exchange

在通信實體之間安全地建立一個共享秘鑰的協商過程。

3、密鑰協商：key agreement

多個用戶之間建立一個共享秘密秘鑰的過程，并且其中任何一個用戶都不能預先確定該秘鑰的值。

4、從A到B的密鑰確認 key comfirmation from A to B

使用戶B確信用戶A擁有特定秘密秘鑰的保證。

5、密鑰派生函數  key derivation function

通過作用于共享秘密和雙方都知道的其他參數，產生一個或多個共享秘密秘鑰的函數。

6、雜湊函數  hash function

將一個比特串映射為一個固定長度比特串的函數，該函數滿足如下性質：

（a）對于任意給定的輸出，要找其對應的輸入，在計算上是不可行的；

（b）對于任意給定的輸入，要找到輸出相同的另一個輸入，在計算上是不可行的。

7、雜湊值  hash value

雜湊函數作用于一條消息時輸出的比特串。

8、對稱密碼算法  symmetric cryptographic algrorithm

一種執行加密/解密的算法，其中加密/解密使用的秘鑰容易從計算上相互求得。

9、發起方  initiator

在一個協議的操作過程中發送首輪交換信息的用戶。

10、響應方  responder

在一個協議的操作過程中不是發送首輪交換信息的用戶。

11、可辨別標識  disdinguishing identifier

可以無歧義辨別某一實體身份的信息。

三、符號

A,B：使用公鑰密碼系統的兩個用戶。

a,b：Fq中的元素，它們定義Fq上的一條橢圓曲線E。

dA：用戶A的私鑰。

dB：用戶B的私鑰。

E(Fq)：Fq上橢圓曲線E的所有有理點（包括無窮遠點O）組成的集合。

Fq：包含q個元素的有限域。

G：橢圓曲線的上一個基點，其階為素數。

Hash()：密碼雜湊函數。

Hv()：消息摘要長度為v比特的密碼雜湊函數。

消息摘要百度百科：

HASH函數的抗沖突性使得如果一段明文稍有變化，哪怕只更改該段落的一個字母，通過哈希算法作用后都將產生不同的值。而HASH算法的單向性使得要找到哈希值相同的兩個不同的輸入消息，在計算上是不可能的。所以數據的哈希值，即消息摘要，可以檢驗數據的完整性。

哈希函數的這種對不同的輸入能夠生成不同的值的特性使得無法找到兩個具有相同哈希值的輸入。因此，如果兩個文檔經哈希轉換后成為相同的值，就可以肯定它們是同一文檔。所以，當希望有效地比較兩個數據塊時，就可以比較它們的哈希值。例如，可以通過比較郵件發送前和發送后的哈希值來驗證該郵件在傳遞時是否修改。

h：余因子，h=#E(Fq)/n，其中n是Fq的階。

IDA，IDB：用戶A和用戶B的可辨別標識。

K，KA，KB：秘鑰交換協議商定的共享秘密秘鑰。

KDF()：秘鑰派生函數。

modn：模n運算。

n：基點G的階（n是#E(Fq）的素因子）。

O：橢圓曲線上的一個特殊點，稱為無窮遠點或零點，是橢圓曲線加法群的單位元。

------------------------------------------分割線在此，不要看我（2016.04.20更新）---------------------------------------------------

PA：用戶A的公鑰。

PB：用戶B的公鑰。

q：有限域Fq中元素的數目。

rA：秘鑰交換中用戶A產生的臨時秘鑰值。

rB：秘鑰交換中用戶B產生的臨時秘鑰值。

x||y：x與y的拼接，其中x與y可以是比特串或字符串。

ZA：關于用戶A的可辨別標識、部分橢圓曲線系統參數和用戶A公鑰的雜湊值。

ZB：關于用戶B的可辨別標識、部分橢圓曲線系統參數和用戶B公鑰的雜湊值。

#E(Fq)：E(Fq)上點的數目，稱為橢圓曲線E(Fq)的階。

|k|P：橢圓曲線上點P的k倍點，k是正整數。

x.y]：大于或等于x且小于或等于y的整數的集合。

頂函數：大于或等于x的最小整數。

底函數：小于或等于x的最小整數。

&：兩個整數按比特與運算。

四、算法參數與輔助函數

1、總則：

密鑰交換協議是兩個用戶A和B通過交互的信息傳遞，用各自的私鑰和對方的公鑰來商定一個只有他們自己知道的秘密密鑰。這個共享的秘密密鑰通常用在某個對稱密碼算法中。該密鑰交換協議能夠用于密鑰管理和協商。

2、橢圓曲線系統參數：

（1）有限域Fq的規模q；

（2）定義橢圓曲線E(Fq)的兩個參數啊，a、b∈Fq；

（3）E(Fq)上的基點G=（xG，yG）（G≠O），其中xG、yG是Fq中的兩個元素；

（4）G的階n及其可選項（如n的余因子h等）。

3、用戶密鑰對

用戶A的密鑰對應包括其私鑰dA和公鑰PA=[dA]G=(xA，yA)，用戶B的密鑰對應包括其私鑰dB和公鑰PB=[dB]G=(xB，yB)。

用戶密鑰對的生成算法與公鑰驗證算法應符合第一部分第六章的規定。

4、輔助函數

（1）密碼雜湊函數：如SM3；

（2）密鑰派生函數：從一個共享的秘密比特串中派生出密鑰數據。在密鑰協商過程中，密鑰派生函數作用在密鑰交換所獲共享的秘密比特串上，從中產生所需要的會話密鑰或進一步加密所需要的秘鑰數據。

密鑰派生函數需要調用秘鑰雜湊函數。

（3）隨機數發生器：使用國密局規定的隨機數發生器。

5、用戶其他信息

五、密鑰交換協議及流程

1、密鑰交換協議

設用戶A和B協商獲取密鑰數據的長度為klen比特，用戶A是發起方，用戶B是響應方。用戶A和B雙方為了獲取相同的密鑰，應實現如下運算步驟：

w=[[log2(n)]/2]-1。（注：此處的[]指的是頂函數）

用戶A：

A1：用隨機數發生器產生隨機數rA∈[1,n-1]；

A2：計算橢圓曲線點RA=[rA]G=（x1，y1）；

A3：將RA發送給用戶B。

用戶B：

B1：用隨機數發生器產生隨機數rB∈[1,n-1]；

B2：計算橢圓曲線點RB=[rB]G=（x2，y2）；

B3：從RB中取出域元素x2，按本文第一部分的4.2.7給出的方法將x2的數據類型轉換為整數，計算x2`=2^w+(x2&(2^w-1))；

B4：計算tB=（dB+x2`*rB）mod n；

B5：驗證RA是否滿足橢圓曲線的方程，若不滿足則協商失敗；否則從從RB中取出域元素x1，按本文第一部分的4.2.7給出的方法將x2的數據類型轉換為整數，

計算x1`=2^w+(x1&(2^w-1))；

B6：計算橢圓曲線點V=[h*tB](PA+[x1`]RA)=(xv,yv)，若V是無窮遠點，則B協商失敗；否則按本文第一部分4.2.5和4.2.4給出的方法將xv，yv的數據類型轉換為比特串；

B7：計算KB=KDF（xv||yv||ZA||ZB，klen）；

B8：（選項）按本文第一部分4.2.5和4.2.4給出的方法將RA的坐標x1、y1和RB的坐標x2、y2的數據類型轉換為比特串，計算SB==Hash.......；

B9：將RB、（選項SB）發送給用戶A；

用戶A：

A4：從RA中提取出域元素x1，按本文第一本分4.2.7給出的方法將x1的數據類型轉換為整數，計算x1`=2^w+(x1&(2^w-1))；

A5：tA=（dA+x2`*rA）mod n；

A6：驗證RB是否滿足橢圓曲線的方程，若不滿足則協商失敗；否則從從RB中取出域元素x2，按本文第一部分的4.2.7給出的方法將x2的數據類型轉換為整數，

計算x2`=2^w+(x2&(2^w-1))；

A7：計算橢圓曲線點U=[h*tA](PB+[x2`]RB)=(xu,yu)，若U是無窮遠點，則A協商失敗；否則按本文第一部分4.2.5和4.2.4給出的方法將xu，yu的數據類型轉換為比特串；

A8：計算KA=KDF（xu||yu||ZA||ZB，klen）；

A9：（選項）計算S1，并檢驗S1=SB是否成立，若不成立則從B到A的秘鑰確認失敗；

A10：（選項）計算SA，并將SA發送給用戶B。

用戶B;

B10：計算S2，并檢驗S2=SA是否成立，若不成立則從A到B的秘鑰確認失敗。

（二）秘鑰交換協議流程

、

————————————————

版權聲明：本文為CSDN博主「qq_30866297」的原創文章，遵循CC 4.0 BY-SA版權協議，轉載請附上原文出處鏈接及本聲明。

原文鏈接：https://blog.csdn.net/qq_30866297/article/details/51194236