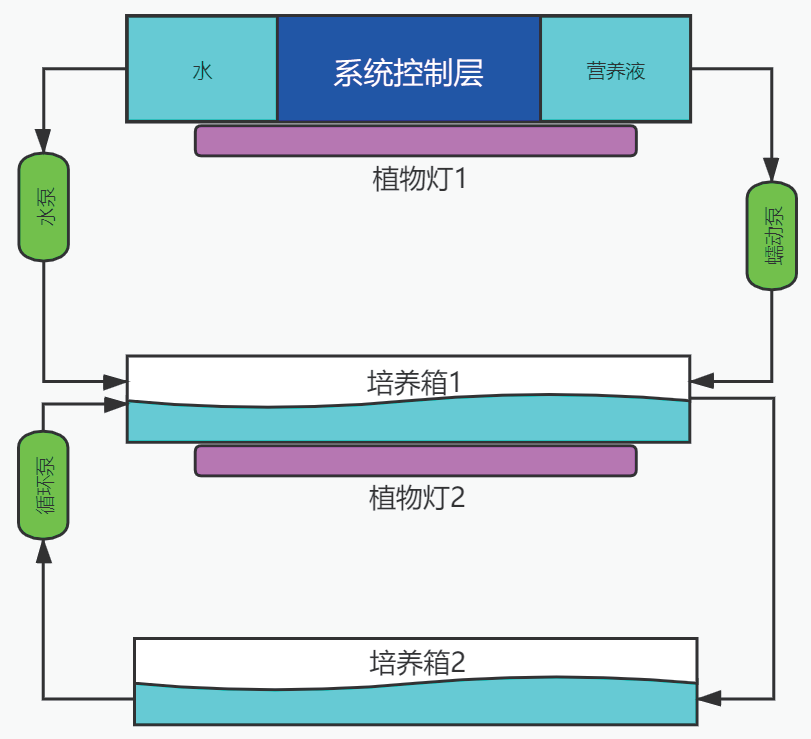
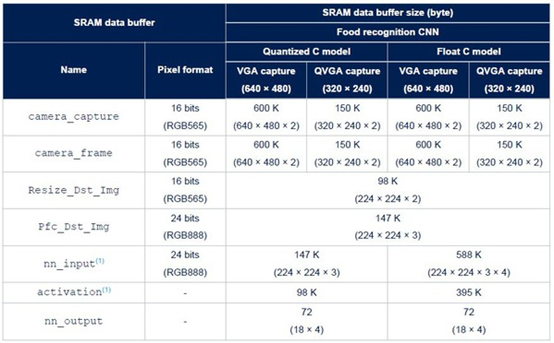
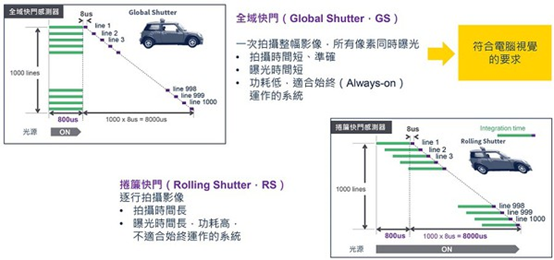
【計算機視覺】什么是直方圖均衡化？

計算機視覺教程之直方圖均衡化原理

1 點算子

點算子是兩個像素灰度值間的映射關系，屬于像素的逐點運算，相鄰像素不參與運算。點算子是最簡單的圖像處理手段，如：亮度調整、對比度調整、顏色變換、直方圖均衡化等等。

2 線性灰度變換

線性灰度變換表達為：

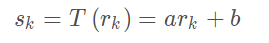
其中$r_k$、$s_k$分別為輸入、輸出點像素灰度值。

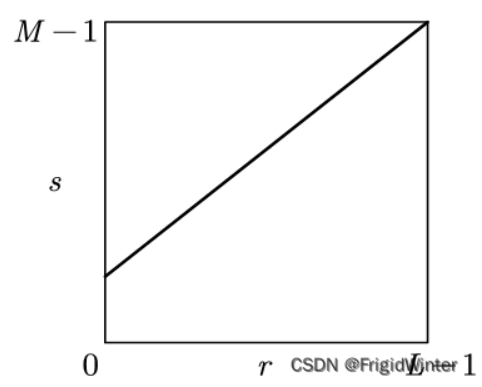
當$a>1$時，輸出圖像像素灰度范圍擴大，圖像對比度增強，當$a<1$時反之。這是因為<font color=#F00>**人眼不易區分相近的灰度值**</font>，因此若圖像灰度值范圍較小，觀感上細節不夠清晰。當$a=1$、$b\ne0$時，點算子使圖像灰度整體上移或下移，即整體變亮或變暗。

3 直方圖均衡化

下圖再次給出了關于圖像對比度的例子

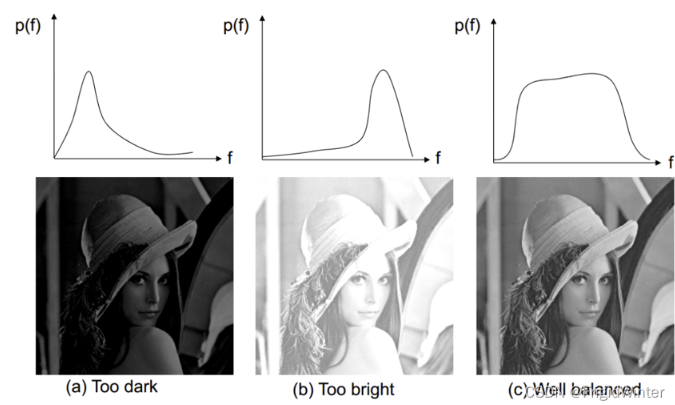
直方圖均衡化是以累計分布函數為核心，將原始圖像灰度直方圖從比較集中的某個灰度區間，非線性地映射為在全部灰度范圍內的較均勻分布，從而增強對比度。

下面闡述直方圖均衡化的數學原理。首先作原始圖像灰度的概率直方圖如圖

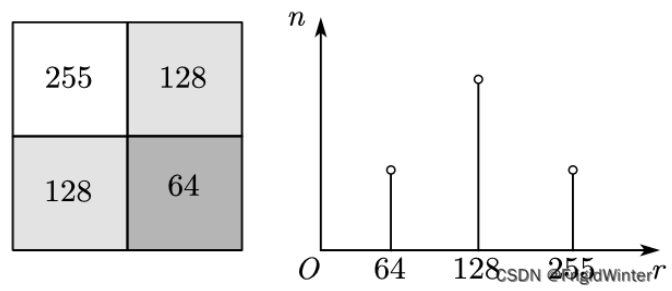
設輸入像素灰度值為$r_k$，累計分布函數為

$$C\left( r_k \right) =\frac{1}{n}\sum_{i=0}^k{n_i}$$

其中$n_i$為圖像中灰度值為$r_i$的像素頻數，$n$為圖像像素總數。設輸出像素灰度值為$s_k$，像素范圍為$s_{min}-s_{max}$。期望輸出灰度直方圖是均勻分布，即

$$P\left( s \right) =\frac{1}{s_{\max}-s_{\min}}\,\,   s_{\min}\leqslant s\leqslant s_{\max}$$

令$C\left( s_k \right) =C\left( r_k \right)$，即得

$$\left( C\left( r_k \right) _{\max}-C\left( r_k \right) _{\min} \right) \frac{s_k-s_{\min}}{s_{\max}-s_{\min}}+C\left( r_k \right) _{\min}=C\left( r_k \right) \\\Rightarrow \,\,                                            \frac{s_k-s_{\min}}{s_{\max}-s_{\min}}=\frac{C\left( r_k \right) -C\left( r_k \right) _{\min}}{C\left( r_k \right) _{\max}-C\left( r_k \right) _{\min}}\\\Rightarrow \,\,                                            \frac{s_k-s_{\min}}{s_{\max}-s_{\min}}=C'\left( r_k \right)$$

所以最終直方圖均衡化的點算子為

$$s_k=\left( s_{\max}-s_{\min} \right) C'\left( r_k \right) +s_{\min}=T\left( r_k \right)$$

# 4 代碼實戰

按照前文的原理編寫累積分布函數計算公式，以及均衡化算子

```python

# 計算累計分布函數

def C(rk):

  # 讀取圖片灰度直方圖

  # bins為直方圖直方柱的取值向量

  # hist為bins各取值區間上的頻數取值

  hist, bins = np.histogram(rk, 256, [0, 256])

  # 計算累計分布函數

  return hist.cumsum()

```

```python

# 計算灰度均衡化映射

def T(rk):

  cdf = C(rk)

  # 均衡化

  cdf = (cdf - cdf.min()) * (255 - 0) / (cdf.max() - cdf.min()) + 0

  return cdf.astype('uint8')

```

<font size=4 color=#000>均衡化時直接調用函數即可，下面給出完整代碼

```python

import numpy as np

import cv2 as cv

from matplotlib import pyplot as plt

# 計算累計分布函數

def C(rk):

  # 讀取圖片灰度直方圖

  # bins為直方圖直方柱的取值向量

  # hist為bins各取值區間上的頻數取值

  hist, bins = np.histogram(rk, 256, [0, 256])

  # 計算累計分布函數

  return hist.cumsum()

# 計算灰度均衡化映射

def T(rk):

  cdf = C(rk)

  # 均衡化

  cdf = (cdf - cdf.min()) * (255 - 0) / (cdf.max() - cdf.min()) + 0

  return cdf.astype('uint8')

# 讀取圖片

img = cv.imread('1.png', 0)

# 將二維數字圖像矩陣轉變為一維向量

rk = img.flatten()

# 原始圖像灰度直方圖

plt.hist(rk, 256, [0, 255], color = 'r')

cv.imshow("原圖像",img)

# 直方圖均衡化

imgDst = T(rk)[img]

cv.imshow("直方圖均衡化后的圖像",imgDst)

plt.hist(imgDst.flatten(), 256, [0, 255], color = 'b')

plt.show()

```

看看效果：

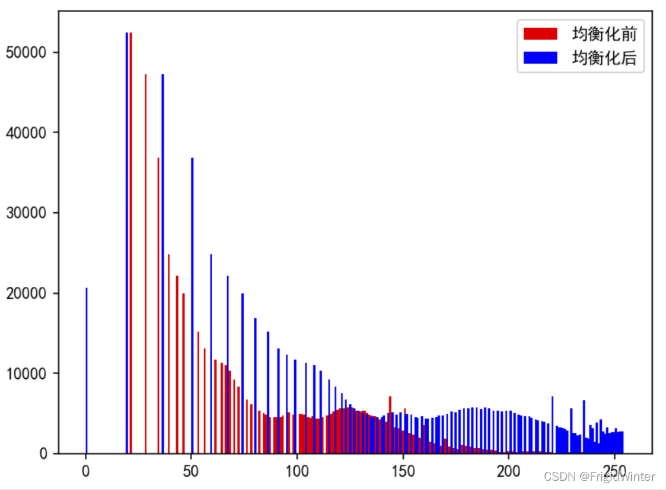
均衡化前：

均衡化后：

更多優質內容、更好的閱讀體驗、完整配套代碼詳見下方公眾號“AI技術社”