2W字長文 | 漫談工業界圖神經網絡推薦系統（1）

圖神經網絡是近年來很火的一個研究方向，在生物化學，推薦系統，自然語言處理等領域都得到了廣泛應用。其中圖神經網絡在推薦系統的應用方面，已有幾篇綜述[1][2][3]做過詳細的歸納總結。但是讓人感到美中不足的是，綜述中總結的多是學術型工作，偏向于GNN模型上的微調，部分工作其實就是將上游的SGC[4]，GrapSage[5]，JKNet[6]等模型在幾個祖傳玩具數據集上刷一下結果講一個故事，很少關心模型的擴展性，也很少關心圖的構建，特征處理，線上打分等不可或缺的環節。

因此本文選取了一些近幾年阿里，騰訊，京東，華為等企業在KDD，SIGIR，CIKM等會議發表的文章，這些工作的實驗至少是在真實業務場景的大規模數據集（千萬級或億級）上進行的，部分工作也成功在線上AB實驗中取得了一些效果。全文分為三部分，第一部分簡單介紹涉及較多的幾個GNN研究方向，包括Deeper GNN（GNN加深），Scalable GNN（大圖訓練），Heterogeneous GNN（異構GNN）；第二部分從幾個不同的角度總結選取的文章，包括應用階段，圖的構建，特征使用，采樣方法，模型結構；第三部分會逐篇介紹這些工作的重點內容。

鏈接：

https://zhuanlan.zhihu.com/p/423342532

1. GNN介紹

不同于傳統的MLP，CNN，RNN等模型，GNN可以建模鄰居順序與數量不定的非歐式數據，常被用來處理結點分類，鏈接預測，圖分類等任務。可以從兩個角度理解GNN，譜圖卷積與消息傳遞，今年我們在ICML的工作則是從迭代算法求解目標函數的角度解釋GNN[7]，同時在該理論框架內還能解釋并解決過平滑，邊的不確定性等問題。針對不同類型的任務，不同類型的圖數據（異質圖，動態圖，異構圖）等，存在許多特定的GNN模型，此外，還有圖的池化，圖預訓練，圖自監督等方向，相關的內容可以參考綜述[8]。第一小節會簡單介紹一些基礎通用且有代表性的GNN模型，后三小節分別介紹Deeper GNN，Scalable GNN和Heterogeneous GNN三個方向，這些都是在將圖神經網絡應用到推薦系統時經常涉及的知識。最后一節談談個人對圖神經網絡的優勢的理解。

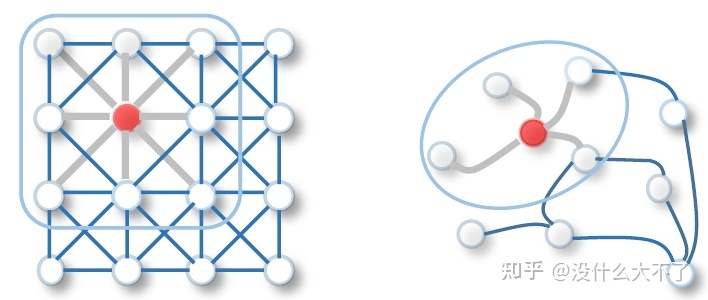
非歐式數據

1.1 Common GNN

常用GNN模型及其貢獻

Spectral CNN[9]：利用拉普拉斯矩陣定義了圖上的卷積算子，其特點如下：

濾波器是全局的。

圖上的細微擾動會導致特征基的變化。

參數的量級是O(n)，與結點數量正相關，難以擴展到大圖。

特征分解的復雜度比較高。

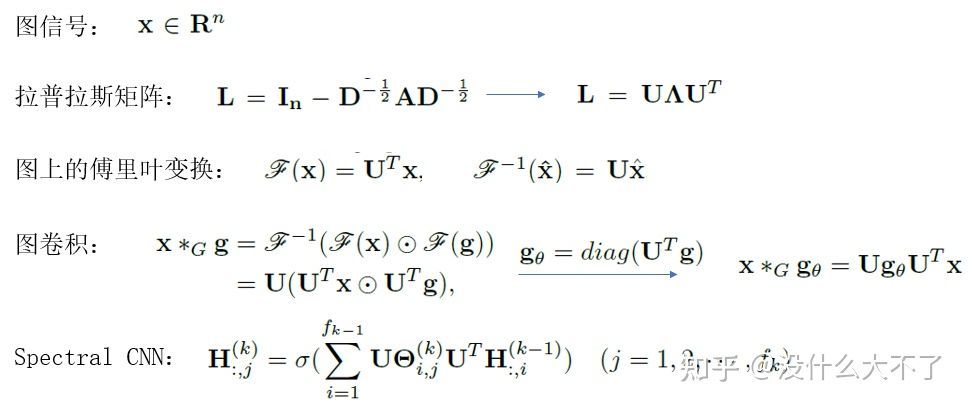
Spectral CNN

ChebNet[10]：利用切比雪夫多項式近似，降低了計算量和參數量，其特點如下：

濾波器是局部的，對應著0-K階鄰居。

參數量的量級是O(K)。

不需要進行特征分解。

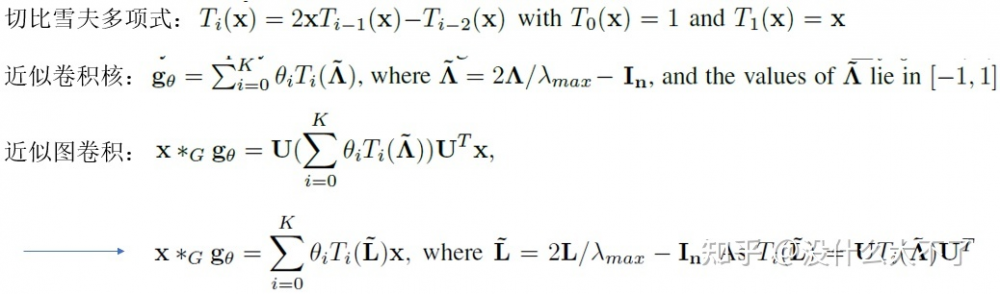
ChebNet

GCN[11]：進一步簡化了ChebNet，將譜圖卷積與消息傳遞聯系起來，其層級結構便于和深度學習結合。

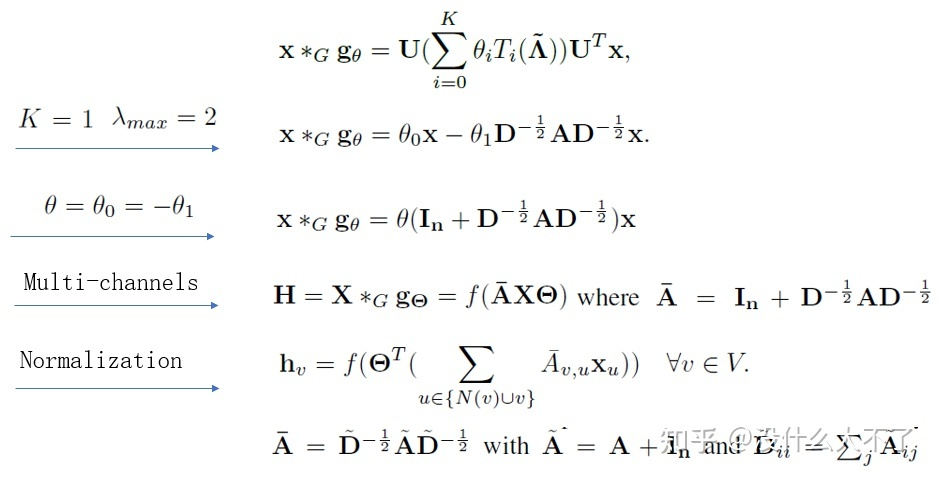
GCN

SGC[4]：解耦了消息傳遞和特征變換， [公式] 部分可以預計算，簡化后仍然可以在大多數數據集上取得和GCN相當的結果。

SGC

GAT[12]：將注意力機制引入GCN，建模了鄰居結點的重要性差異，增強了模型的表達能力。

GAT

GraphSage[5]

一方面，將消息傳遞框架范式化，分為Aggregate（聚合鄰居）和Concat（融合自身）兩個步驟。

GraphSage

另一方面，提出了一種簡單有效的鄰居采樣方法，可以在大圖上進行Mini-Batch訓練，并且當有新的結點加入時，不需要在全圖上聚合鄰居，也不需要重新訓練模型，可以用訓練好的模型直接推斷。

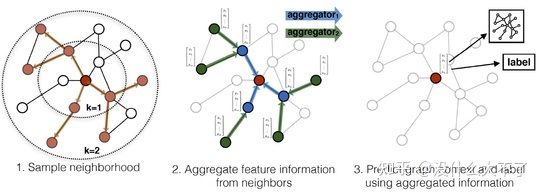
Node-Wise Sampling

PPNP[13]：同樣采用消息傳遞和特征變換分離的結構，并基于個性化PageRank改進消息傳遞，使模型可以平衡局部和全局信息。

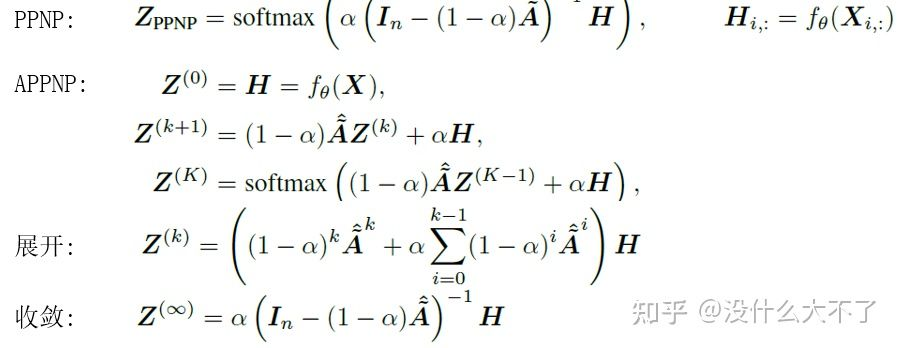
PPNP

RGCN[14]：對于不同類型的邊對應的鄰居結點采用不同的參數矩陣從而建模邊的異構性。當邊的類型很多時，參數也會變得很多，容易造成過擬合，并且不易訓練，需要對參數進行規約，使用了一下兩種方式：

Bias decomposition（定義一組基向量）不僅可以減少參數量，同時對于那些樣本較少的邊也能得到充分學習（參數共享）。

Block-diagnoal decomposition只能減少參數量，實驗下來效果也不如Bias decomposition。

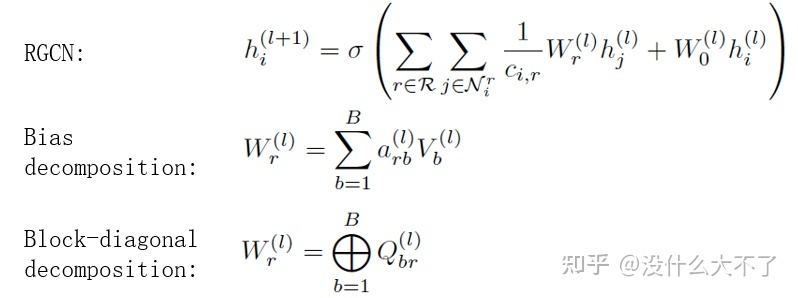
HAN[15]：將GAT擴展到了異構圖上，不僅考慮了不同鄰居結點的重要性差異，也考慮了不同語義的meta-path的重要性差異。

對于鄰居結點的重要性，例如，考慮meta-path：Paper-Author-Paper以及結點分類任務，Paper A、C是數據庫算法論文，Paper B是圖神經網絡論文，它們都是Author A的發表的文章，即PaperB、C都是Paper A的鄰居，但是在聚合時顯然Paper C與Paper A更相關，需要給與更大的權重。

對于meta-path的重要性，例如，考慮meta-path：Paper-Author-Paper以及Paper-Institution-Paper，通常同一個作者發表的文章，比同一個機構產出的文章更相關。

HAN

1.2 Deeper GNN

1.2.1 問題背景

在GCN的實驗中發現[11]，一般2-3層的GCN可以取得最好的性能，繼續增加層數GCN的性能會開始下降，達到8層以上會發生大幅度的下降。

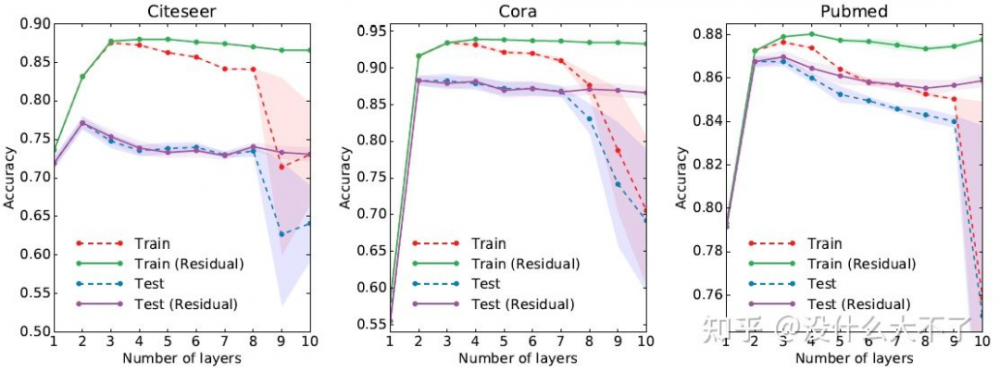
GCN無法加深

1.2.2 理論分析

研究者證明了，隨著SGC（不考慮層間的非線性）層數的加深，所有結點會收斂到同一個表征（簡單的線性代數知識可證）[16]。直觀上看，一個K層的SGC相當于聚合了K-Hop的鄰居特征，當K大于或等于圖的直徑時，每個結點都聚合了整張圖上所有結點的特征，從而每個結點都會收斂到同一個表征，結點之間自然會變得難以分辨。該現象被稱為過平滑問題。

也有人證明了，隨著GCN（考慮層間的非線性）層數的加深，所有結點的表征會收斂到同一個子空間[17]。

也有工作表示，消息傳遞和特征變換的耦合才是阻礙GCN加深的主要原因，不過并沒有從理論上證明只是通過實驗進行了驗證[18]。

1.2.3 個人吐槽

實際上不考慮層之間的非線性時，不斷加深SGC的層數甚至達到80層，只要給予模型更多的Epoch訓練，整體上最終結果并不會有什么下降，這與很多論文里報告的SGC加深到10層以上效果驟降根本不符合。隨著層數的增加，所有結點確實會收斂到同一個表征，然而這需要非常深，只要計算機底層表示的精度能夠區分結點的差異，SGC的效果就不會有什么下降，無非是模型需要更多Epoch訓練收斂。感興趣的同學可以實驗驗證一下。

1.2.4 加深意義

既然2-3層的效果最好，為什么還非要加深呢？這個問題不少工作都不太關心，它們的實驗結果也很一般，只是緩解了加深過程的下降，并沒有帶來什么額外的收益。一種說法是，加深可以增強模型的表達能力（真是個萬能理由），就像CNN那樣通過加深提升效果。比較靠譜的兩種說法是，一是加深可以學習更高階的鄰居信息，這也是不少GNN4Rec工作提到的，高階信息蘊含了多跳的關聯。JKNet中細致分析了中心結點和邊緣結點的情況，如下圖所示，邊緣結點的鄰居非常稀疏，需要加深獲取更大范圍的鄰居信息。二是對于半監督結點分類任務來說，通過加深GCN建立長距離的依賴，可以將帶標簽結點的Label信息傳播給更多結點。

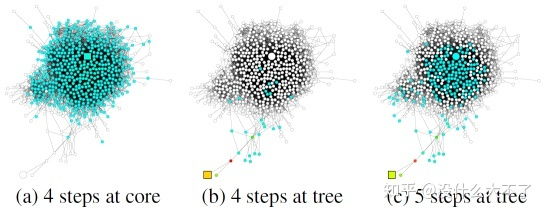
不同位置結點對鄰居范圍的要求

1.2.5 代表工作

Deeper GNN的許多工作，只是緩解了加深的性能下降，并沒有通過加深帶來正向收益。以下是幾個確實可以通過加深提升模型效果的工作。整體上看，比較有效的方法都是在以不同的方式組合不同范圍的鄰居信息，類似于Inception組合不同的感受野。PPNP[13]相當于引入了先驗“近距離的鄰居更重要，并且鄰居的重要性隨距離指數衰減”，DAGNN[19]則是通過不同Hop的聚合結果去學習潛在的重要性分布。

JKNet[6]：GCN的第K層包含了K-Hop范圍的鄰居信息，只使用最后一層的輸出存在過平滑問題，因此JKNet保留了每一層的輸出結果，最后綜合融合不同范圍的鄰居信息。

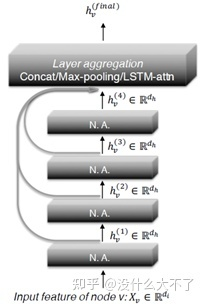
JKNet

PPNP[13]：采用消息傳遞和特征變換分離的結構，并基于個性化PageRank改進消息傳遞，使模型可以平衡局部和全局信息。

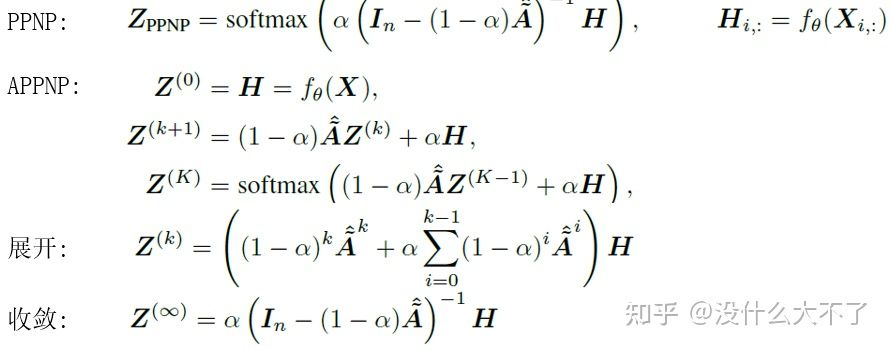
PPNP

GCNII[20]：除了使用個性化PageRank改進消息傳遞，還引入了Residual Connections保持恒等映射的能力。

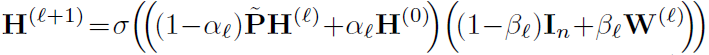
GCNII

DAGNN[19]：自適應地學習不同范圍的鄰居信息的重要性。

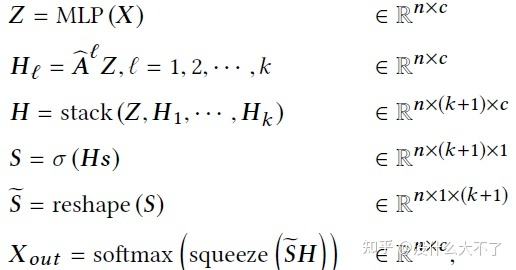
DAGNN