時間序列的自回歸理論和實現

來源：DeepHub IMBA

本篇文章結構如下：

1. 自回歸-理論和數學

2. 在Python中實現的自動回歸

3. 自回歸-選擇最好的參數值

4. 結論

自回歸

術語 AutoRegression (AR) 與來自統計的常規回歸密切相關。唯一的問題是 AR 模型使用來自相同輸入變量的滯后格式數據——這就是 AutoRegression 的 Auto 部分。

AutoRegression 的預測能力有限，就像簡單的移動平均線一樣。該算法使用過去值的線性組合來進行未來預測。一般的 AutoRegression 模型用以下公式表示：

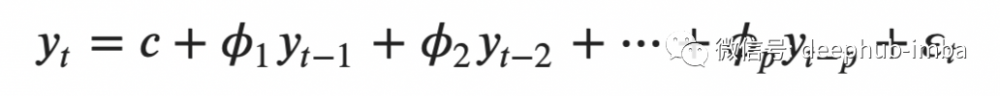
其中 c 是常數，phi 是 p 階以下的滯后系數，epsilon 是不可約誤差（白噪聲）。

使用 AR 模型時，您只需要指定參數 p 的值。如果 p=1，則 AR 模型公式簡化為：

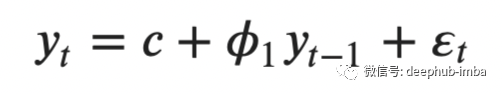
就這么簡單！

p 的更高階數往往會給出更好的預測結果，但僅限于某個點。稍后您將看到如何自動為 p 選擇最佳值。但首先，讓我們看看如何用 Python 實現 AutoRegression。

在 Python 中的實現自回歸

您今天將創建自己的數據集。這是一條簡單的直線，添加了一點噪音：

import numpy as np
 import pandas as pd
 from sklearn.metrics import mean_squared_error
 from statsmodels.tsa.ar_model import AR
 import matplotlib.pyplot as plt
 from matplotlib import rcParams
 from cycler import cycler
 rcParams['figure.figsize'] = 18, 5
 rcParams['axes.spines.top'] = False
 rcParams['axes.spines.right'] = False
 rcParams['axes.prop_cycle'] = cycler(color=['#365977'])
 rcParams['lines.linewidth'] = 2.5
 # Create
 np.random.seed(2)
 xs = np.arange(0, 500, 5)
 ys = [x + np.random.random() * 10 for x in xs]
 df = pd.DataFrame(data={
     'x': xs,
     'y': ys
 })
 # Plot
 plt.title('Random dataset', size=20)
 plt.plot(df['y']);

這是它的樣子：

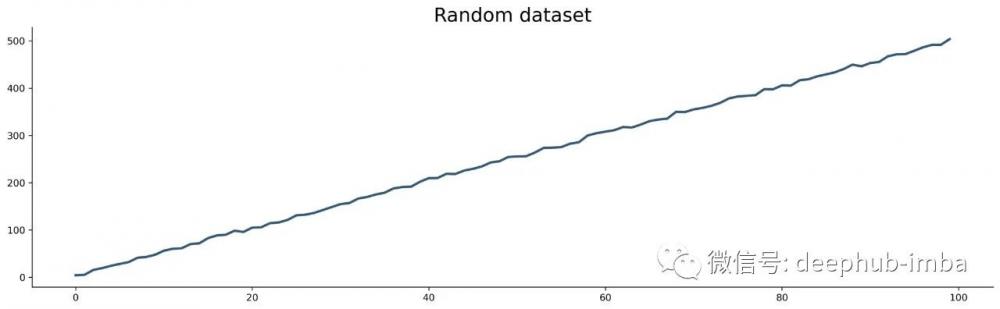
下一步是將數據集劃分為訓練和測試子集。 將使用最后 10 個數據點進行測試，并使用其他所有數據進行訓練：

# Train/test split
 df_train = df[:-10]
 df_test = df[-10:]
 # Plot
 plt.title('Random dataset train and test sets', size=20)
 plt.plot(df_train['y'], label='Training data')
 plt.plot(df_test['y'], color='gray', label='Testing data')
 plt.legend();

以下是兩個數據集的樣子：

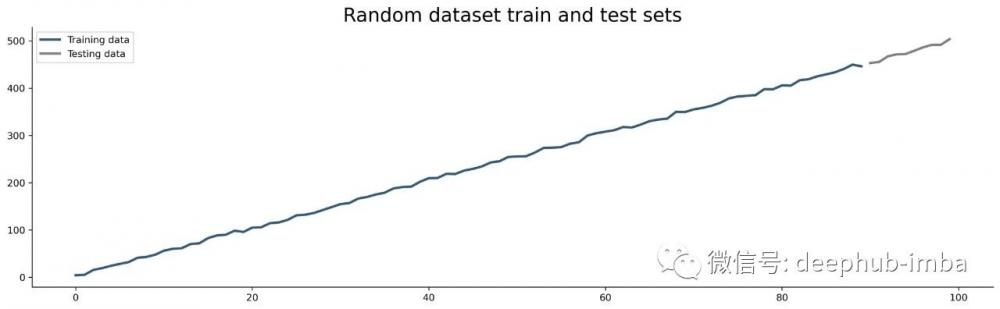
接下來，將聲明一個用于訓練和可視化 AR 模型的函數 — train_and_plot(maxlag: int)。此功能在這里是為了方便，以避免一遍又一遍地復制粘貼幾乎相同的代碼。它在訓練集上訓練 AR(p=maxlag) 模型，并以圖形方式比較預測和測試集。

該函數還會在繪圖副標題中打印模型系數，因此您可以根據需要將它們與之前討論的數學公式聯系起來。

這是代碼：

 def train_and_plot(maxlag):
     model = AR(df_train['y']).fit(maxlag=maxlag, method='mle')
     forecasts = model.predict(
         start=len(df_train),
         end=len(df_train) + len(df_test) - 1,
         dynamic=False
    )
     parameters = model.params.to_dict()
     for k, v in parameters.items():
         parameters[k] = np.round(v, 3)
     plt.title(f'AR({maxlag}) training/testing data and forecasts', size=20, y=1.1)
     plt.suptitle(parameters, y=0.94)
     plt.plot(df_train['y'], label='Training data')
     plt.plot(df_test['y'], color='gray', label='Testing data')
     plt.plot(forecasts, color='orange', label='Forecasts')
     plt.legend();

現在可以使用此函數通過在新單元格中執行 train_and_plot(maxlag=1) 來訓練簡單的 AR(1) 模型。它顯示下圖：

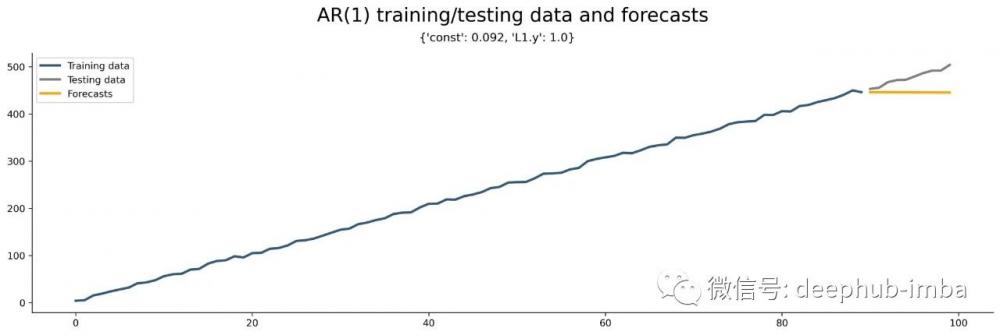
將參數 p 更改為想要的任何內容。例如，AR(2) 模型結果如下所示 (train_and_plot(maxlag=2))：

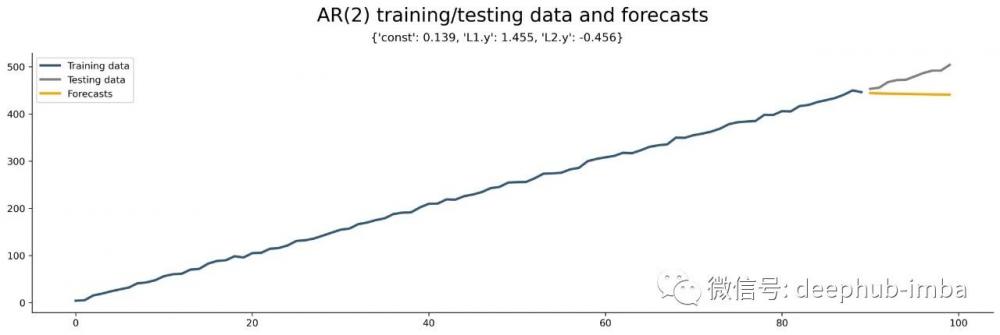
問題仍然存在——這個數據集的最佳 AR 模型順序是什么？讓我們在下一節中回答這個問題。

AutoRegression - 選擇最佳參數值

使用 AR(1) 和 AR(2) 獲得的預測看起來并不那么有希望。你總是想優化 p 的值。一種方法是繪制自相關圖和偏自相關圖并對其進行檢查，但這工作量太大。

更好的方法是在循環內訓練 AR(1) 到 AR(n) 模型，并跟蹤測試集的性能。可以使用 RMSE 或任何其他指標來執行此操作。

這是一個簡單的代碼片段，可以做到這一點：

 # Max lag order
 max_p = 10
 # To store RMSE
 errors = {}
 for p in range(1, max_p + 1):
     # Train and predict
     model = AR(df_train['y']).fit(maxlag=p, dynamic=False)
     preds = model.predict(
         start=len(df_train),
         end=len(df_train) + len(df_test) - 1,
         dynamic=False
    )
     # Calculate and store RMSE
     error = mean_squared_error(df_test['y'], preds, squared=False)
     errors[f'AR({p})'] = error

以下是 AR(1) 到 AR(10) 模型的誤差：

看起來 AR(5) 模型在測試集上的誤差最低。以下是數據集和預測在此模型順序中的樣子：

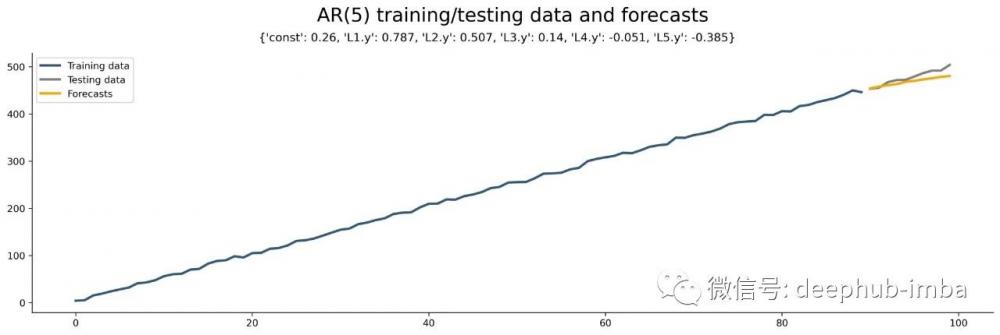
使用 AIC 指標進行評估也很常見，因為它更傾向于簡單的模型而不是復雜的模型。這兩個指標都表明 AR(5) 是最好的模型。

總結

可以使用 AR 模型來預測簡單的數據集。該算法與移動平均模型結合使用時效果最佳，這是我們將在下一篇文章中討論的主題。

如果您決定將 AR 模型應用于 Airline Passengers 等數據集，則無論模型順序如何，都不會獲得良好的預測結果。使數據集靜止可能會有所幫助，但預測仍然不如指數平滑法。