獨家 | 115個A/B測試的分析結果︰平均提升為4%，大部分缺乏統計檢定力(1)

作者 : Georgi Georgiev

翻譯：Gabriel Ng

校對：張玲

從115個公開的A/B測試中你能夠得到什么信息？通常情況下并不會太多，原因在于大部分情況下，你只能看到有關被測對象的基本數據和A/B測試結果。另一方面，置信區間、p值以及其他針對不確定性的度量則往往被遺忘，而即使有，它們的計算也不盡人意，又或者背后的統計過程沒有分享出來，使得它們實際上難以使用。一個數據來源︰GoodUI.org有稍微好一點的方法，在他們網站上發布的每一個測試都附上了基本的統計信息︰用戶數量、每個測試變量的轉換以及被試對象是什么。

筆者決定收集這些數據，并對這115個測試（在下文展示）進行統計上的元分析。除了對A/B測試或轉換率優化活動的樣本的平均結果作出總結以外，這樣做更多的是為了在設計和分析A/B測試時，能作為一個更好的統計習慣的指引。

一個主要發現是相對于預期的結果和成本經濟邏輯，大約70%的測試有著低下的檢定力，暗示著有自選停止的問題。經過數據修剪和統計上的調整后，余下的85個測試顯示出4%以下的平均值和中位數相對提升，當中統計顯著的平均值為6.78%，中位數為5.96%。

因為GoodUI這個樣本并不能代表所有完成的A/B測試，所以對于整個A/B測試流程的任何形式的一般化都應該謹慎處理。

筆者首先會討論初始數據必要的修剪，然后分享元分析的詳細結果，最后作出一個簡短的總結。

統計意義上的重新計算和數據修剪

GoodUI上的數據有對統計顯著度的計算和置信區間，同時也有結果的自評︰"不顯著"、"有可能"、"顯著"、"強"，兩個方向都有。數據也包含了所觀察到的百分比改變。因為有報告的樣本大小，也能對檢定力作出計算。

以百分比變化形式展示，整個數據集的觀察效應估計分布如下︰

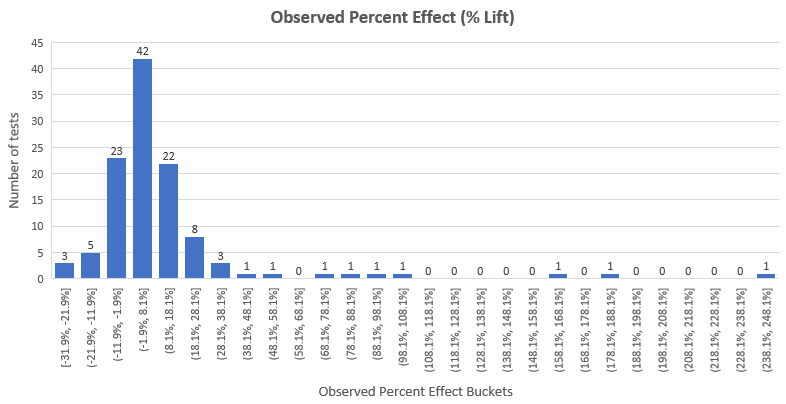
我們可以看到，結果幾乎服從正態分布，效應提升的平均值在12.33%，除了右邊有重尾分布。這個問題我們在下面的文章會展開討論。效應提升的中位數是4.89%，代表著在50%的測試中觀測到的效應提升小于4.89%，而真實的效應提升可能更小。注意這里也包含了那些沒有通過95%顯著性檢驗的測試的觀察效應提升。

統計顯著度和置信區間的重新計算

很不幸的是，在人工提取每個測試的用戶數目和轉換后，筆者需要優先重新計算統計顯著度(p值)和置信區間的上下限，原因是網站上的統計信息有兩個問題︰

1. 顯著度和置信區間的計算都是以雙邊對立假設，而非單邊對立假設作為基本，而在進行方向性的推斷時，顯然單邊對立假設更合理。

2. p值(統計顯著度)和置信區間是為了計算絕對差異，但推斷目標卻是百分比改變（百分比提升）。因此，筆者用了恰當的p值和置信區間來表示百分比提升。

第一個重新計算有著較預期少的不確定性，而第二個重新計算則有著較預期高的不確定性。整體上，相較原來的顯著性水平和置信區間，重新計算使得不確定性減少，原因在于單邊對立假設的修正抹除了百分比提升的改正。

我們可以看到，115個測試中有18個測試結果重新評級︰

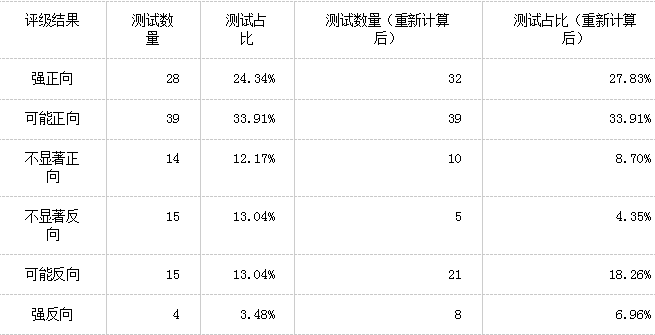
根據GoodUI的定義，有︰

p值小于等于0.03為強結果，p值小于等于0.25為可能結果，p值大于0.25為不顯著結果。每一個評級結果都是連續的（例如若果p值為0.01，則測試的評級不能同時為強和可能）。GoodUI也定義了每個評級所需要的樣本大小，但這是不合理的，因為p值的恰當計算包括了樣本大小的調整，這比GoodUI粗略的做法來得好。

按照更為經典的p值閾值︰0.05（95%置信度），我們獲得了45個統計上顯著的成功結果和12個統計上顯著的失敗結果（分別為整體測試的39.13%和10.43%），余下的58個測試（50.44%）則有著不顯著的結果。恰當p值的分布如下︰

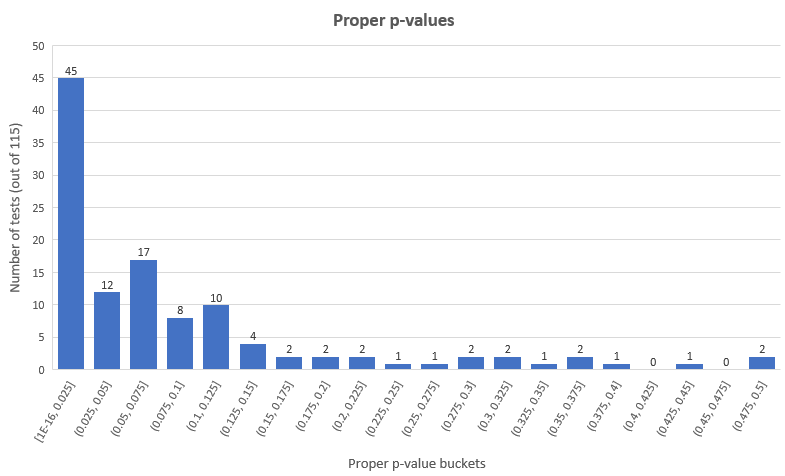
這是p值在0.05以下的測試的觀測效應，恰當計算后，提升效應百分比的單尾p值如下：

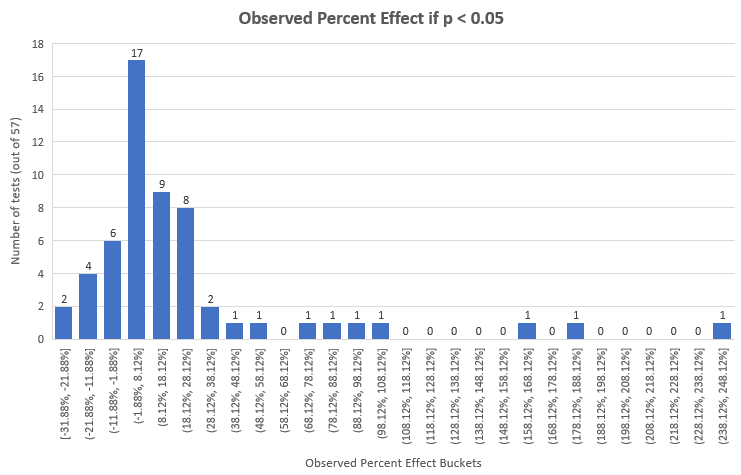
當然，比起整體，這些測試有著較高的平均值和中位數︰22.94%和7.91%，但它們只占115個中的57個。

不平衡測試的移除

115個的測試中的3個（#55，#72，#90）在對照組和實驗組的用戶數目上有著顯著的不平衡。在第一個情景中，相較于對照組（樣本大小為每組200,000+），實驗組有著16%更多的用戶數，而在其后的兩個情景中，分別為9%和13%更少的用戶數（樣本大小為20,000+和10,000+）。我們可以猜測以下原因︰不恰當的隨機化、技術問題引致一部分用戶沒有體驗整體實驗、采用了如多臂老虎機或在測試期間重新平衡臂的類似方法等等。

唯一合理的解釋是隨機化過程中，實驗組和對照組流量分配不均，數量如此之多，以至于筆者懷疑就是這么回事。

如果原因是以上任何一種不合理的解釋，那么很明顯地任何以這一數據為基本的統計分析都會是帶有偏差的。由于出現了妥協性隨機化，并且筆者高度懷疑有意的不均等分布，筆者決定在最后的分析中移除以上3個測試。

明顯妥協性測試的移除

在對A/B測試進行統計設計和分析時，一個常見的問題是在沒有任何統計上的調整下，多次地重復窺探數據，以獲得所需要和希望的數據。這種方法一般被稱為︰”顯著度等待”。

只需幾次觀察就能大大地提高顯著(名義上的)結果的似然性好幾倍，即使真實的觀察可能性非常低。舉個例子，一個有著實際上0.08p值的測試，在經過5次窺探后，就可以得到一個名義上的0.025 p值，這里實際上的p值大大偏離了0.05閾值，且是名義上的p值的3.2倍。現在我們有多種方法去觀察收集數據，而其中一種是”敏捷A/B測試方法”。

發現妥協性測試的一種方法是尋找檢定力低得不切實際的測試。我們可以通過詢問自己以下問題來達到這一效果︰如果我正在設計測試時，考慮到干預的規模、 X%真實提升的預期效益、固定成本、可變成本等等，我會對什么樣的功效水平感到滿意（在文章Risk vs. Reward in A/B Tests: A/B testing as Risk Management一文中有詳細介紹怎樣選擇合適的樣本大小檢定力和顯著性水平）。

舉例說，沒有人會在變量只有輕微改變（例如按鈕的內容文字）的情況下，去設計一個有著90%檢定力，去偵測20%相對變化的測試。在這種情況下，去預期干預有著巨大程度的結果是不現實的，也會因為測試的檢定力低下而白白浪費測試資源。所以當人們在決定合理樣本大小和最小可檢測效應時，一個應該自問的問題是︰怎么樣的結果是令我們鼓舞的？是1%，2%，5%，還是20%？問題的答案因測試而異，但在A/B測試中很少會高于10%。

因為上述原因，合理的設計者不會在大于40%的最小可檢測效應（Minimum detectable effect, MDE）情況下，設計有著90%檢定力的A/B測試，原因是這會使得偵測任何低于MDE的真實效應的機會變得非常低。這一點從熟悉的”效應大小/檢定力函數”的圖像中就能看到。

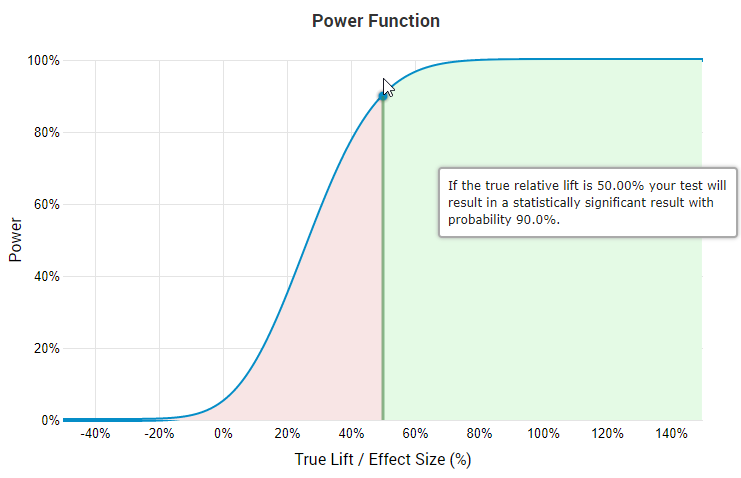
如果真實相對提升為50%，那么根據圖像，測試會有90%的機會有著顯著結果。

上圖來源是A/B測試統計計算器，在圖中能看到如果要以90%檢定力去偵測50%的真實提升，那么只有45.7%的可能性偵測到25%的真實提升，且對于越小的真實效應，其可能性也越小。筆者并不對在這些水平下仍經濟上合理的測試感興趣。而且對于大部分測試，即使是在數據修剪前效應大小的中位數也有著4%-5%。這進一步說明在顯著高的水平下設計有著最小可檢測效應的測試是不合理的。

所以如果我們希望在115個測試中偵測出妥協性測試，在90%檢定力下，觀測測試效應大小的分布是一個值得的舉動。下圖是實際結果（平均最小可檢測提升是27.8%，中位數是20.84%）︰

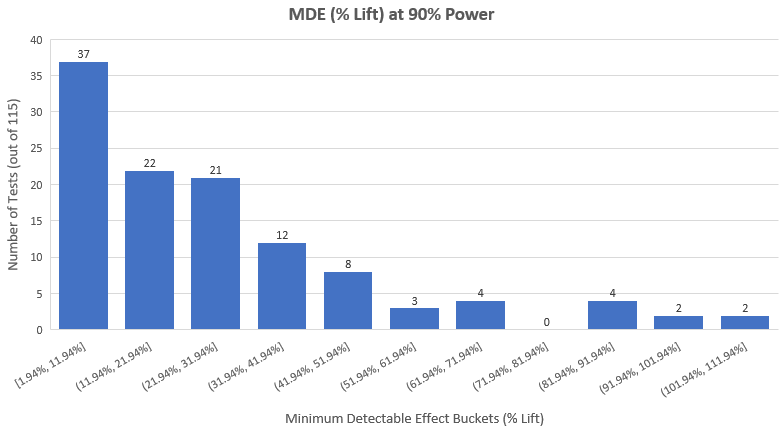
第一眼就明顯的情況是︰

1. 有一大堆測試，它們的設計者認為測試有天文級別的改善效果。

2. 有一大堆測試，只有在天文級別高的結果下才經濟合算。

3. 有一大堆人在沒有固定樣本大小的前提下進行測試，而且常常窺探數據，最后若無其事地分析結果。

筆者認為情況3最有機會代表大部分的測試。即使沒有像情況3那樣做，他們也是用了某種恰當的相繼性分析。正確的測試是這樣的︰p值的計算吻合固定樣本大小測試的計算結果，而且它們只有在固定樣本大小的測試下才變得合理。

通過對每一個測試的干預進行人工檢視，結合筆者對于在這些干預中的合理效應大小的知識，以及A/B測試的經濟效益。筆者得出了自己（某程度上的主觀）的評估結果，在115個測試中的80個（69.57%）是低檢定力的，從而筆者懷疑當中有不同程度的自選停止。這里，筆者必須指出其假設已經是相當寬松的。

雖然如此，筆者仍無意為了闡釋評估結果中的主觀部分，而單單對30個測試作出分析，故筆者決定只移除最為明顯的出錯例子︰在90%檢定力和0.05（95%信賴度）顯著水平的情況下，有著最小可檢測提升為大于等于40%的測試。注意，筆者在檢定力的計算中已是十分寬松，因為在GoodUI的分類中，p值的閾值為0.03，而不是0.05。

數據修剪的結果是，有25個測試被移除，因未解釋的自選停止（數據窺探）下而出現了明顯的妥協行為。因為沒有關于窺探次數和時間的信息，我們沒有辦法去對p值和信賴區間作出調整以抵償數據的窺探。被移除的總測試數變成28（當中3個是因為不平衡的樣本大小），可供分析的測試有87個。