IJCAI 2021 | 一文了解微軟亞洲研究院機器學習方向前沿進展（1）

編者按：第30屆國際人工智能聯合大會 IJCAI 2021 于8月19日-26日在線上正式召開。此次大會共收到4204篇投稿，其中587篇論文被接收，接收率為13.9%。在本屆會議中，微軟亞洲研究院也有多篇論文入選，今天我們精選了其中的5篇來為大家進行簡要介紹。歡迎大家積極參與文末的投****活動，我們將邀請大家最感興趣的論文的作者進行深度講解，與大家線上交流！

01 利用獨立性的優勢函數估計方法

論文鏈接：

https://www.ijcai.org/proceedings/2021/0461.pdf

在強化學習中，優勢函數  (advantage function)  普遍采用蒙特卡洛  (MC)、時間差分  (TD)，以及一種將前兩者結合的優勢函數估計算法（GAE)  等進行估計，而這些算法都存在方差較高的問題。因此，微軟亞洲研究院的研究員們首次提出通過利用環境中存在于當前動作和未來狀態之間的獨立性，來降低優勢函數估計中的方差。

在該方法中，存在于環境中的獨立性可以用來構建一個基于重要性采樣 (importance sampling) 的優勢函數估計量。該估計量可以忽略未來無關的部分獎勵，從而減小估計中的方差。為了進一步減少優勢函數估計的方差，研究員們把該估計量和已有的蒙特卡洛估計量進行融合，并將最終的優勢函數估計量命名為 IAE (Independence-aware Advantage Estimation)。實驗結果表明，在策略優化算法中，IAE 與現有的優勢函數估計方法  (GAE, MC)  相比，達到了更高的樣本利用率。

事實上，現有方法往往先估計值函數 Q(s,a) 和 V(s)，再將二者相減，進而估計優勢函數。但當值函數覆蓋的時間范圍較大時，估計值函數就需要考慮未來較長時間內的總獎勵，因此導致了高方差的問題。

當環境中存在獨立性時，優勢函數的估計就不需要考慮環境中的部分獎勵，從而使得估計中的方差減小。舉個例子：假設智能體當前的任務是打乒乓球，在該環境下，智能體每贏得一分或輸掉一分后，游戲的狀態都會被重新設置到起始狀態，并繼續進行下一輪游戲。當對智能體每一個動作的優勢函數進行估計時，由于智能體每個動作的影響都被限制在當前回合內，所以下一輪及之后的獎勵實質上不影響優勢函數的估計。

上述例子表明，如果執行當前的動作不影響未來某些狀態的概率，那么這些未來狀態上的獎勵在估計優勢函數時就可以被忽略。研究員們對上述觀察進行了概括和抽象，并提出了基于重要性采樣的優勢函數估計量。下面給出的是基于重要性采樣推導出來的該估計量的形式：

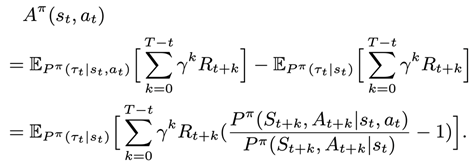
此公式證明了如下的估計量是優勢函數的無偏估計量：

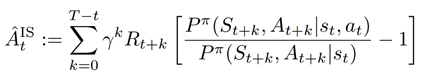
在后續推導中，研究員們進一步將上述基于重要性采樣的估計量與基于蒙特卡洛的優勢函數估計量進行結合，并通過優化結合后估計量的方差，使優勢函數估計的方差更小。同時，研究員們將組合后的優勢函數估計量命名為 IAE，并在實驗中測量了 IAE  的估計性能。最后，研究員們還提出了上述公式中重要性采樣的概率比值的估計方法，并且還利用其對該概率比值進行了準確的估計。

在 tabular 設置下，研究員們構建了多種包含3個狀態的馬爾可夫決策過程 (MDP)，并且在這些設置中包含了不同的轉移函數設置和不同的獎勵設置。研究員們比較了  IAE、蒙特卡洛、重要性采樣三種優勢函數估計量在不同設置下的標準差，結果見表1。實驗結果表明，IAE 的估計量的標準差顯著小于蒙特卡洛和重要性采樣的估計量的標準差。

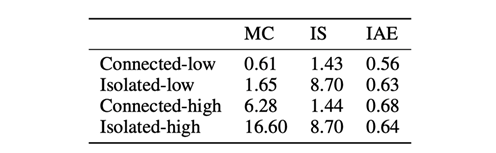
表1：不同設置下 IAE、MC、IS 的標準差

為了驗證 IAE 在策略優化中的作用，研究員們將 IAE、蒙特卡洛、GAE 分別作為 PPO 算法中的優勢函數估計方法，使用 PPO 算法進行策略優化，并觀察不同優勢函數估計方法在策略優化中的性能。該實驗使用高維圖像作為狀態，即智能體的策略和優勢函數的估計均只使用圖像輸入。PPO 算法在不同優勢函數估計方法下的訓練曲線圖1，兩幅圖對應于兩種不同的獎勵設置。實驗結果表明，IAE 作為優勢函數估計算法時，策略優化過程的樣本利用率更高。

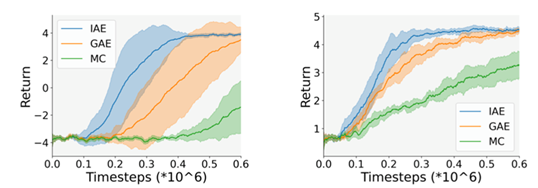
圖1：PPO 算法在不同優勢函數估計方法下的訓練曲線

02 面向合作與非合作任務的多智能體強化學習方法MFVFD

論文鏈接：

https://www.ijcai.org/proceedings/2021/0070.pdf

多智能體強化學習（Multi-agent Reinforcement Learning, MARL） 有望幫助解決各種現實世界中的問題。然而，追求有效的MARL 面臨著兩大挑戰：部分可觀察性和可擴展性限制。為了應對這兩大挑戰，并使得 MARL 適用于競爭任務、合作任務以及混合任務，微軟亞洲研究院和北京大學的研究員們在中心訓練分散執行（Centralized Training with Decentralized Execution，CTDE）的框架下，從個體值函數分解 （Value Function Decomposition，VFD）的角度，結合平均場理論（Mean Field Theory，共同提出了一種新穎的多智能體 Q 學習方法——MFVFD。

正所謂“非宅是卜，唯鄰是卜”，如果鄰里和睦，則利人利己；而鄰里不和，則多是非。也就是說，在多智能體系統中，個體不僅要考量最大化自身的利益，也要考量其臨近智能體的行為對齊本身的影響。比如，在足球環境中，球員射門得分與否，除去依賴球員個體自身的射門能力之外，還會受到近鄰智能體的影響，即優秀的隊友與糟糕的對手會促進得分，而糟糕的隊友和優秀的對手則會阻礙得分。

為了研究多智能體如何在既有合作又有競爭的環境下的表現，研究員們基于平均場理論將個體在多智能體系統中基于全局信息的動作值函數，近似為基于局部信息估計的個體動作值函數與基于近鄰信息的平均場影響函數的和，公式如下：

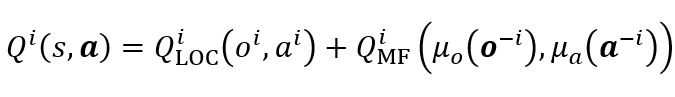
其中，Q_LOC^i 為基于局部信息的個體 i 的動作值函數，用于動作選擇；Q_MF^i 為基于近鄰信息的平均場影響函數，用于輔助對 Q_LOC^i 的估計。考慮到智能體不同近鄰的重要性不同，所以研究員們使用注意力機制（Attention）建立了單體與近鄰的權重 λ^i (o^i,o^k,a^i,a^k)，并基于此計算帶有重要性權重的近鄰觀測分布  μ_o (o^(-i) ) 和動作分布 μ_a (a^(-i) ) ，以構建平均場影響函數 Q_MF^i。

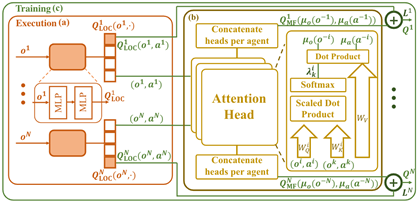
圖2：MFVFD 網絡結構圖

在主試驗部分，研究員們選取了 MAgent Battle 任務，對 MFVFD 在具有大規模智能體且具有部分觀測的限制下的性能進行了驗證。在該任務中，紅藍雙方各具有400個智能體，每個智能體具有局部觀測，且無法通訊，其通過消滅敵人來獲得獎勵。由于每個智能體以優化各自的獎勵為目標，所以單體會與同伴競爭殺敵數量，來獲取更多的個人獎勵。除此之外，單體還會與同伴配合避免被殺害，以消滅所有敵人獲取更多的團隊獎勵。因此，這是一個合作和競爭混合的復雜任務。如圖3所示，MFVFD（紅色）與基線方法的（藍色）相比，學會了更難的團體配合的圍殲策略，取得了勝利。從對抗勝率上可以看出，MFVFD 在所有的基線方法中，幾乎處于不敗地位。

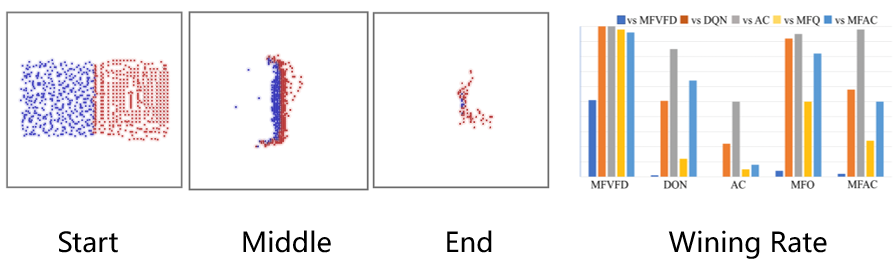
圖3：MFVFD 與基線方法相比

此外，研究員們還選取了三個任務對 MFVFD 方法進行了理論分析，分別是：重復矩陣博弈任務----鷹鴿博弈與非單調合作博弈；合作導航任務----Cooperative Navigation；交通任務----Traffic Benchmark。從長遠來看，MFVFD 在實際環境中能夠有實際可行的研究價值。