綜述：輕量級CNN架構設計（1）

以下文章來源于GiantPandaCV ，作者Ironboy

作者丨Ironboy

來源丨GiantPandaCV

編輯丨極市平臺

導讀

本文作者結合論文和項目比賽的經驗，講述了輕量級CNN的發展以及設計總結。內容包含基本概念、卷積計算類型、其他算子、常用激活函數、經典輕量化模型等。

卷積神經網絡架構設計，又指backbone設計，主要是根據具體任務的數據集特點以及相關的評價指標來確定一個網絡結構的輸入圖像分辨率，深度，每一層寬度，拓撲結構等細節。

公開發表的論文大多都是基于ImageNet這種大型的公開數據集來進行的通用結構設計，早期只以其分類精度來證明設計的優劣，后來也慢慢開始對比參數量(Params)和計算量(FLOPs)，由于ImageNet的數據量十分巨大且豐富，所以通常在該數據集上獲得很好精度的網絡結構泛化到其他任務性能也都不會差。

但在很多特定任務中，這種通用的結構雖然效果還可以，卻并不算最好，所以一般在實際應用時通常是基于已公開發表的優秀網絡結構再根據任務特點進行適當修改得到自己需要的模型結構。

目前人工智能技術應用的一個趨勢是在端側平臺上部署高性能的神經網絡模型并能在真實場景中實時(大于30幀)運行，如移動端/嵌入式端設備。這些平臺的特點是內存資源少，處理器性能不高，功耗受限，這使得目前精度最高的模型由于對內存和計算資源的超額要求使得根本無法在上面部署且達到實時性的要求。雖然可以通過知識蒸餾，通道剪枝，低比特量化等一系列手段來降低模型參數量和計算量，但仍然遠遠不夠，且在精度和幀率之間各種trade-off也非常繁瑣。所以直接設計輕量級的架構，然后結合剪枝量化是最有效的解決辦法。

本文將結合自己看的論文和參加項目比賽的經驗講述輕量級CNN的發展以及一些設計總結，如有不對之處請不吝賜教。

基本概念

· 感受野(Receptive Field)

感受野指的是卷積神經網絡每一層輸出的特征圖(feature map)上每個像素點映射回輸入圖像上的區域大小，神經元感受野的范圍越大表示其能接觸到的原始圖像范圍就越大，也意味著它能學習更為全局，語義層次更高的特征信息，相反，范圍越小則表示其所包含的特征越趨向局部和細節。因此感受野的范圍可以用來大致判斷每一層的抽象層次，并且我們可以很明顯地知道網絡越深，神經元的感受野越大。

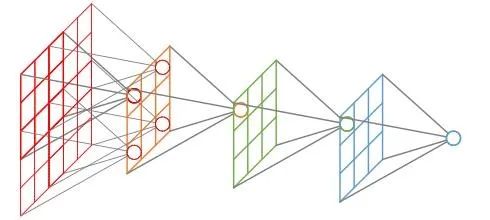
感受野

· 分辨率(Resolution)

分辨率指的是輸入模型的圖像尺寸，即長寬大小。通常情況會根據模型下采樣次數n和最后一次下采樣后feature map的分辨率k×k來決定輸入分辨率的大小，即：

r=k*2ⁿ

從輸入r×r到最后一個卷積特征feature map的k×k，整個過程是一個信息逐漸抽象化的過程，即網絡學習到的信息逐漸由低級的幾何信息轉變為高級的語義信息，這個feature map的大小可以是3×3，5×5，7×7，9×9等等，k太大會增加后續的計算量且信息抽象層次不夠高，影響網絡性能，k太小會造成非常嚴重的信息丟失，如原始分辨率映射到最后一層的feature map有效區域可能不到一個像素點，使得訓練無法收斂。

在ImageNet分類任務中，通常設置的5次下采樣，并且考慮到其原始圖像大多數在300分辨率左右，所以把最后一個卷積特征大小設定為7×7，將輸入尺寸固定為224×224×3。在目標檢測任務中，很多采用的是416×416×3的輸入尺寸，當然由于很多目標檢測模型是全卷積的結構，通常可以使用多尺寸訓練的方式，即每次輸入只需要保證是32×的圖像尺寸大小就行，不固定具體數值。但這種多尺度訓練的方式在圖像分類當中是不通用的，因為分類模型最后一層是全連接結構，即矩陣乘法，需要固定輸入數據的維度。

· 深度(Depth)

神經網絡的深度決定了網絡的表達能力，它有兩種計算方法，早期的backbone設計都是直接使用卷積層堆疊的方式，它的深度即神經網絡的層數，后來的backbone設計采用了更高效的module(或block)堆疊的方式，每個module是由多個卷積層組成，它的深度也可以指module的個數，這種說法在神經架構搜索(NAS)中出現的更為頻繁。通常而言網絡越深表達能力越強，但深度大于某個值可能會帶來相反的效果，所以它的具體設定需要不斷調參得到。

· 寬度(Width)

寬度決定了網絡在某一層學到的信息量，但網絡的寬度時指的是卷積神經網絡中最大的通道數，由卷積核數量最多的層決定。通常的結構設計中卷積核的數量隨著層數越來越多的，直到最后一層feature map達到最大，這是因為越到深層，feature map的分辨率越小，所包含的信息越高級，所以需要更多的卷積核來進行學習。通道越多效果越好，但帶來的計算量也會大大增加，所以具體設定也是一個調參的過程，并且各層通道數會按照8×的倍數來確定，這樣有利于GPU的并行計算。

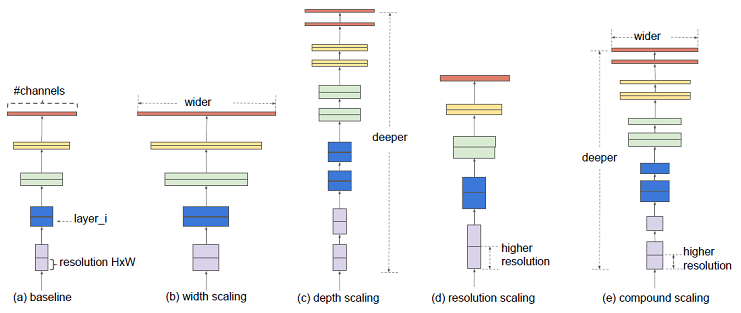
width,depth and resolution

· 下采樣(Down-Sample)

下采樣層有兩個作用，一是減少計算量，防止過擬合，二是增大感受野，使得后面的卷積核能夠學到更加全局的信息。下采樣的設計有兩種：

1.采用stride為2的池化層，如Max-pooling或Average-pooling，目前通常使用Max-pooling，因為它計算簡單且最大響應能更好保留紋理特征；

2.采用stride為2的卷積層，下采樣的過程是一個信息損失的過程，而池化層是不可學習的，用stride為2的可學習卷積層來代替pooling可以得到更好的效果，當然同時也增加了一定的計算量。

(突然想到為啥不使用雙線性插值，向下插值來代替Pooling，這個雖然比MaxPooling計算量更大，但是保留的信息應該更豐富才是)

· 上采樣(Up-Sampling)

在卷積神經網絡中，由于輸入圖像通過卷積神經網絡(CNN)提取特征后，輸出的尺寸往往會變小，而有時我們需要將圖像恢復到原來的尺寸以便進行進一步的計算(如圖像的語義分割)，這個使圖像由小分辨率映射到大分辨率的操作，叫做上采樣，它的實現一般有三種方式：

插值，一般使用的是雙線性插值，因為效果最好，雖然計算上比其他插值方式復雜，但是相對于卷積計算可以說不值一提；

轉置卷積又或是說反卷積，通過對輸入feature map間隔填充0，再進行標準的卷積計算，可以使得輸出feature map的尺寸比輸入更大；

Max Unpooling，在對稱的max pooling位置記錄最大值的索引位置，然后在unpooling階段時將對應的值放置到原先最大值位置，其余位置補0；

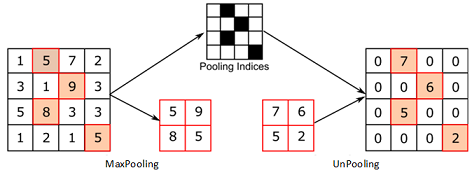
Max Unpooling

· 參數量(Params)

參數量指的網絡中可學習變量的數量，包括卷積核的權重weight，批歸一化(BN)的縮放系數γ，偏移系數β，有些沒有BN的層可能有偏置bias，這些都是可學習的參數 ，即在模型訓練開始前被賦予初值，在訓練過程根據鏈式法則中不斷迭代更新，整個模型的參數量主要由卷積核的權重weight的數量決定，參數量越大，則該結構對運行平臺的內存要求越高，參數量的大小是輕量化網絡設計的一個重要評價指標。

· 計算量(FLOPs)

神經網絡的前向推理過程基本上都是乘累加計算，所以它的計算量也是指的前向推理過程中乘加運算的次數，通常用FLOPs來表示，即floating point operations(浮點運算數)。計算量越大，在同一平臺上模型運行延時越長，尤其是在移動端/嵌入式這種資源受限的平臺上想要達到實時性的要求就必須要求模型的計算量盡可能地低，但這個不是嚴格成正比關系，也跟具體算子的計算密集程度(即計算時間與IO時間占比)和該算子底層優化的程度有關。

卷積計算類型

· 標準卷積 (Convolution)

在神經網絡架構設計中，標準卷積是最常見的結構，假設其輸入feature map的維度是(1, iC, iH, iW)，每個卷積核的維度是(1, iC, k, k)，一次卷積濾波得到一層feature map的維度為(1,1, oH, oW)，一共有oC個卷積核，則輸出feature map的維度是(1, oC, oH, oW)，計算量為iC×k×k×oC×oH×oW，計算過程如下圖所示，由于太過基礎，故不贅述。

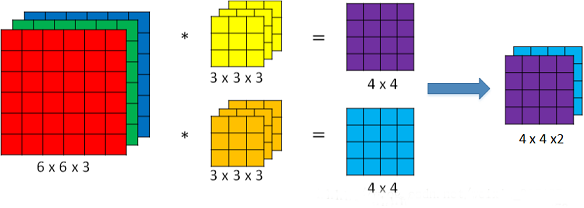
標準卷積

· 深度卷積 (Depthwise Convolution)

深度卷積與標準卷積相比，顧名思義是在深度上做了文章，而這里的深度跟網絡的深度無關，它指的通道，標準卷積中每個卷積核都需要與feature map的所有層進行計算，所以每個卷積核的通道數等于輸入feature map的通道數，通過設定卷積核的數量可以控制輸出feature map的通道數。而深度卷積每個卷積核都是單通道的，維度為(1,1,k,k) ，卷積核的個數為iC，即第i個卷積核與feature map第i個通道進行二維的卷積計算，最后輸出維度為(1,iC,oH,oW)，它不能改變輸出feature map的通道數，所以通常會在深度卷積后面接上一個(oC,iC,1,1)的標準卷積來代替3×3或更大尺寸的標準卷積，總的計算量為k×k×iC×oH×oW+iC×1×1×oH×oW×oC，是普通卷積的1/oC+1/(k×k)，大大減少了計算量和參數量，又可以達到相同的效果，這種結構被稱為深度可分離卷積(Depthwise Separable Convolution)，在MobileNet V1被提出，后來漸漸成為輕量化結構設計的標配。

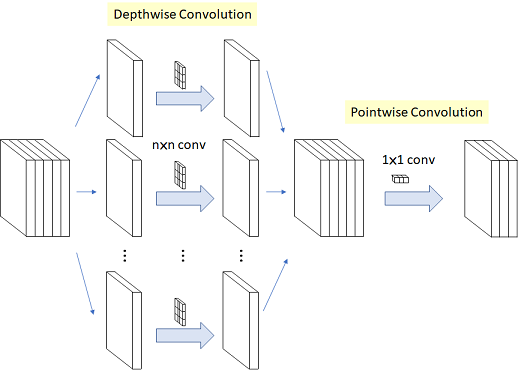
深度可分離卷積

深度卷積之前一直被吐槽在GPU上運行速度還不如一般的標準卷積，因為depthwise 的卷積核復用率比普通卷積要小很多，計算和內存訪問的比值比普通卷積更小，因此會花更多時間在內存開銷上，而且per-channel的矩陣計算很小不容易并行導致的更慢，但理論上計算量和參數量都是大大減少的，只是底層優化的問題。

· 分組卷積 (Group Convolution)

分組卷積最早在AlexNet中出現，當時作者在訓練模型時為了減少顯存占用而將feature map分組然后給多個GPU進行處理，最后把多個輸出進行融合。具體計算過程是，分組卷積首先將輸入feature map分成g個組，每個組的大小為(1, iC/g, iH, iW)，對應每組中一個卷積核的大小是(1,iC/g,k,k)，每組有oC/g個卷積核，所以每組輸出feature map的尺寸為(1,oC/g,oH,oW)，最終g組輸出拼接得到一個(1,oC,oH,oW)的大feature map，總的計算量為iC/g×k×k×oC×oH×oW，是標準卷積的1/g，參數量也是標準卷積的1/g。

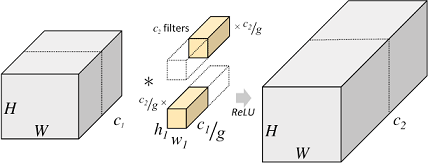
分組卷積

但由于feature map組與組之間相互獨立，存在信息的阻隔，所以ShuffleNet提出對輸出的feature map做一次channel shuffle的操作，即通道混洗，打亂原先的順序，使得各個組之間的信息能夠交互起來。