基于非平衡態(tài)熱力學(xué)的全新三維點云生成模型,北大這項研究提名CVPR 2021最佳論文
本文介紹了北京大學(xué)王選計算機研究所胡瑋老師課題組本科生羅世通的工作,這篇論文提出了基于非平衡態(tài)熱力學(xué)的全新三維點云生成模型,并獲得 CVPR2021 的最佳論文提名。

論文鏈接: https://arxiv.org/abs/2103.01458
代碼地址: https://github.com/luost26/diffusion-point-cloud
課題組主頁:https://www.wict.pku.edu.cn/huwei/
早期的三維點云生成模型將點云簡單地視為一個 N*3 維的高維向量,其中 N 代表點云中點的數(shù)量。點云生成問題被轉(zhuǎn)化為了一個 N*3 維向量的生成問題。這使得許多常用的生成模型能夠直接應(yīng)用到點云生成中。雖然這類方法成功實現(xiàn)了點云的生成,但是它們存在兩大缺陷:首先,由于訓(xùn)練好的生成模型只能生成固定維數(shù)的向量,因此這些模型生成的點云點數(shù)也只能是固定的;其次,由于這些模型將 N 個點的三維坐標(biāo)以固定的順序排列在一起構(gòu)成一個 N*3 維向量,點與點之間無形之中被賦予了先后次序,排序不變性這一三維點云的重要性質(zhì)被破壞了。由于點與點之間被賦予了順序,神經(jīng)網(wǎng)絡(luò)不得不去學(xué)習(xí)如何泛化到不同的排序上,最終影響了模型的生成效果。
為了解決上述問題,研究者們分別獨立提出了 FoldingNet 和 AtlasNet。它們將點云表示為一個從二維矩形區(qū)域到三維空間的映射,并且用神經(jīng)網(wǎng)絡(luò)來實現(xiàn)這一映射。直覺上來看,這個映射就是把一張二維的 “紙片” 折成立體的結(jié)構(gòu),這也正是 FoldingNet 名字的含義。盡管這類方法實現(xiàn)了任意點數(shù)的點云生成以及滿足了點云的排序不變性質(zhì),它們?nèi)匀痪哂幸恍┤毕? 首先,這些模型的損失函數(shù)采用了 Chamfer 距離或者 Earth Mover 距離。計算這兩種距離需要引入兩個點云之間點與點的對應(yīng)關(guān)系,但是這種對應(yīng)關(guān)系并不是天然存在的,只能人為構(gòu)造,所以這兩種距離并不能最真實地反映兩個點云之間的差距。另一方面,從實踐上看,以 Chamfer 距離(CD)作為損失函數(shù)訓(xùn)練出來的生成模型,其生成的點云密度常常不均勻。對于 Earth Mover 距離(EMD),由于計算這一距離所需要的一一對應(yīng)關(guān)系只能通過近似的方式找到,所以常常會有較大的誤差,導(dǎo)致訓(xùn)練效果受到影響。
近期比較新穎的一種觀點是將三維點云視為來自于某個三維概率分布的一組樣本,這一觀點啟發(fā)了另一條研究思路:使用非參數(shù)估計工具去擬合點云的三維概率分布。PointFlow 使用連續(xù)歸一化流擬合三維分布,連續(xù)歸一化流最大的缺陷在于速度很慢,因為其前向傳播和反向傳播都需要對一個連續(xù)函數(shù)進行數(shù)值積分,運行一次數(shù)值算法方法往往需要對神經(jīng)網(wǎng)絡(luò)進行幾十甚至上百次求值。
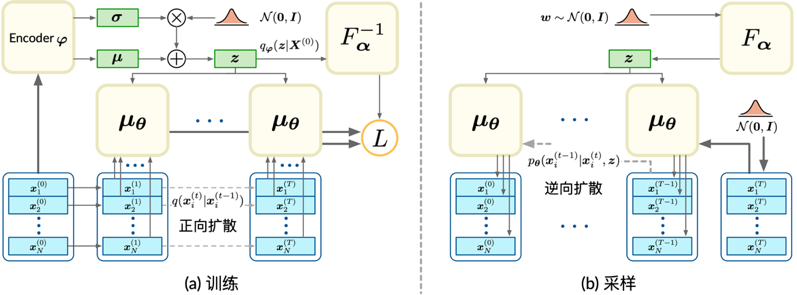
本文提出了一種全新的三維點云生成模型。受到非平衡態(tài)熱力學(xué)中的「擴散過程」概念啟發(fā),這項研究將具備一定形態(tài)的點云視為熱力學(xué)系統(tǒng)中的粒子。具備一定形態(tài)的點云中的點隨著時間的推移,會在空間中擴散開來,點的分布從集中有序走向分散無序。為了生成點云,本文考慮建模擴散過程的逆過程——將分散無序的點集逐步恢復(fù)為具有一定形態(tài)的點云,點的分布從分散走向集中。為了實現(xiàn)這一逆擴散過程,本文者提出了一種基于有限長度馬爾可夫鏈的模型。只要該馬爾可夫鏈經(jīng)過恰當(dāng)?shù)挠?xùn)練,初始位置服從高斯分布的點集在該馬爾可夫鏈的引導(dǎo)下進行隨機游走,最終會集中于有意義的位置,構(gòu)成有意義的形狀。研究者構(gòu)造了上述馬爾可夫鏈模型的一種具體實現(xiàn),并且導(dǎo)出了訓(xùn)練該模型的優(yōu)化目標(biāo)函數(shù),最終通過實驗展現(xiàn)了上述方法在三維點云自編碼、生成以及無監(jiān)督表示學(xué)習(xí)等基礎(chǔ)任務(wù)上的優(yōu)越性能。
相比之下,本文提出的方法具有較大的優(yōu)勢。首先,本文提出的方法支持生成任意點數(shù)的點云,且確保了點之間的排序不變性。和基于 GAN 的方法相比,本方法只需要對馬爾可夫鏈的轉(zhuǎn)移核進行訓(xùn)練,訓(xùn)練損失函數(shù)形式非常簡單,而 GAN 需要同時對生成器、判別器兩部分進行訓(xùn)練,且損失函數(shù)形式復(fù)雜,不穩(wěn)定。和基于連續(xù)歸一化流以及能量模型的方法相比,本方法速度快,且模型表達能力更強,因為本方法對網(wǎng)絡(luò)結(jié)構(gòu)沒有任何限制,而歸一化流要求網(wǎng)絡(luò)可逆,限制了表達能力。
具體來說,這項研究的貢獻主要有:
提出了一種基于非平衡態(tài)熱力學(xué)擴散過程的三維點云生成模型。
給出了該模型的一種具體實現(xiàn)方案,該方案包含用于實現(xiàn)該模型的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)、基于變分推斷的訓(xùn)練損失函數(shù)、高效的訓(xùn)練算法、采樣算法四部分。
通過實驗表明了該模型在點云生成、自編碼、無監(jiān)督表示學(xué)習(xí)上取得了優(yōu)越的性能。
方法
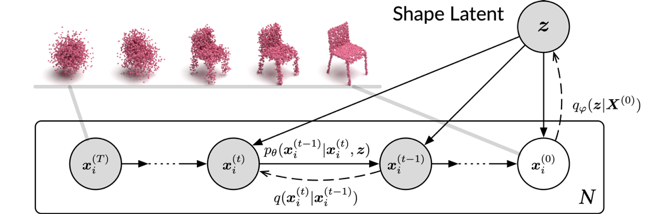
我們借助逆擴散過程建模三維點云。如上圖所示,我們使用馬爾可夫鏈建模點云的逆擴散過程,并且使用神經(jīng)網(wǎng)絡(luò)參數(shù)化馬爾可夫鏈的轉(zhuǎn)移核。轉(zhuǎn)移核是一個條件概率分布,它根據(jù)點當(dāng)前的位置決定下一步所在位置的分布。為了使模型能夠生成不同形狀的點云,我們額外引入一個形狀隱變量 z,在具體實現(xiàn)上,我們使用歸一化流參數(shù)化 z 的先驗分布,增強模型的表達能力。
根據(jù)概率圖可知,由于存在隱變量,我們無法直接使用最大似然估計訓(xùn)練模型,因此,我們轉(zhuǎn)而通過最大化似然函數(shù)的證據(jù)誤差下界(ELBO)來訓(xùn)練模型。
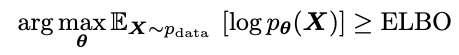
生成點云主要包括三個步驟:(1)首先從形狀隱變量的先驗分布中采樣一個形狀變量 z;(2)然后在三維標(biāo)準(zhǔn)高斯分布中采樣一個點集 X^(T);(3)最后在以 z 為條件,在馬爾可夫鏈迭代采樣,直到得到 X^(0),即生成的點云。
實驗結(jié)果
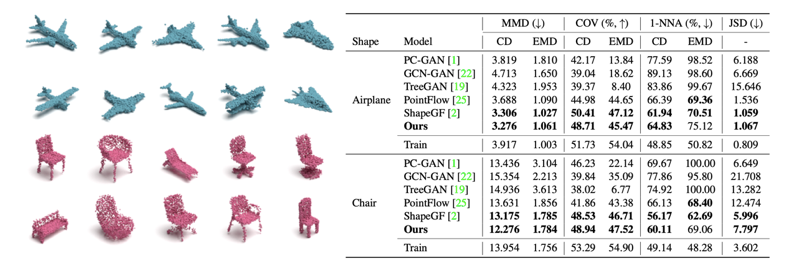
本文提出的模型在三個基準(zhǔn)任務(wù)上達到了優(yōu)越的性能:(1)點云生成;(2)點云自編碼;(3)無監(jiān)督表示學(xué)習(xí)。
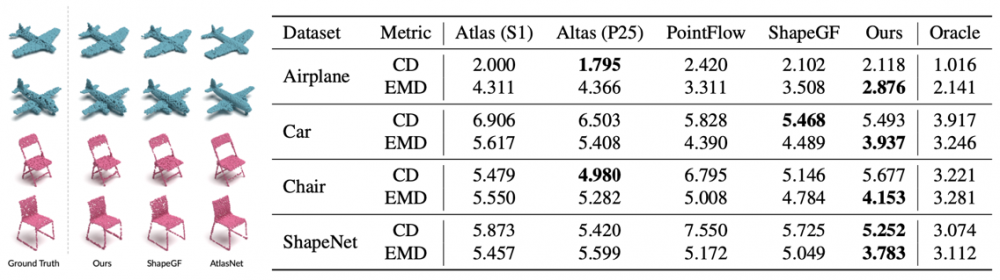
下圖展示了部分生成的點云以及不同點云生成模型之間的定量比較:
下圖展示了不同點云自編碼器重建的點云以及不同模型點云自編碼性能的定量比較:
下圖展示了自編碼器隱空間插值結(jié)果:

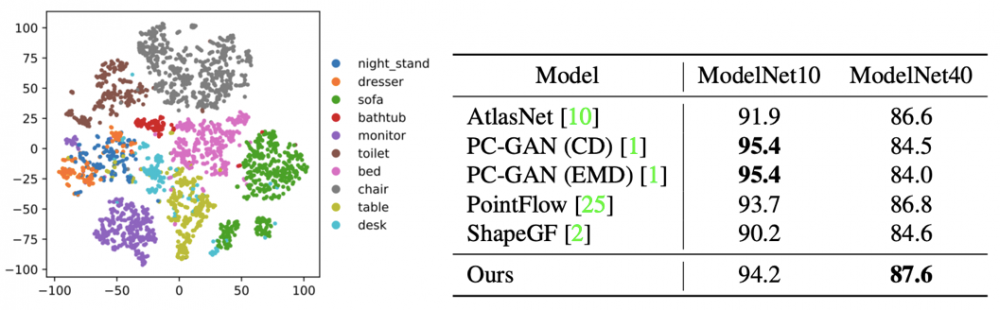
下圖為自編碼器對不同形狀的編碼的 tSNE 可視化,可以看出,不同類別的點云編碼區(qū)別清晰。我們進一步使用線性 SVM 對編碼進行分類,我們的模型在更大規(guī)模的 ModelNet40 數(shù)據(jù)集上準(zhǔn)確率顯著高于其它方法:
參考文獻
Panos Achlioptas, Olga Diamanti, Ioannis Mitliagkas, and Leonidas Guibas. Learning representations and generative models for 3d point clouds. In International conference on machine learning, pages 40–49. PMLR, 2018.
Ruojin Cai, Guandao Yang, Hadar Averbuch-Elor, Zekun Hao, Serge Belongie, Noah Snavely, and Bharath Hariharan. Learning gradient fields for shape generation. arXiv preprint arXiv:2008.06520, 2020.
Jonathan Ho, Ajay Jain, and Pieter Abbeel. Denoising diffusion probabilistic models. arXiv preprint arXiv:2006.11239, 2020.
GuandaoYang,XunHuang,ZekunHao,Ming-YuLiu,Serge Belongie, and Bharath Hariharan. Pointflow: 3d point cloud generation with continuous normalizing flows. In Proceedings of the IEEE International Conference on Computer Vision, pages 4541–4550, 2019.
Diederik P Kingma and Max Welling. Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114, 2013.
Yaoqing Yang, Chen Feng, Yiru Shen, and Dong Tian. Foldingnet: Point cloud auto-encoder via deep grid deformation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 206–215, 2018.
*博客內(nèi)容為網(wǎng)友個人發(fā)布,僅代表博主個人觀點,如有侵權(quán)請聯(lián)系工作人員刪除。








