開關電容梳狀濾波器幅頻特性的深入分析

　　3 頻域法特性分析

　　開關周期切換，形成的RC并聯(lián)支路對外電路的等效電流ie(t)為：

　　上式說明，Ie(Ω)是輸入電流頻譜I(Ω)周期延拓的組合，周期為Ω0=2π／T。各電流分量流過RC并聯(lián)支路時的電壓為相應電流分量與RC支路阻抗(R／(1+jωτ)，ω=Ω±(2n+1)π／T)的乘積，于是輸出電壓頻譜U(Ω)為：

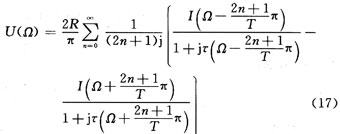
　　為求系統(tǒng)頻譜函數，取i(t)=-ui(t)／R1=-δ(t)／R1，I(Ω)=-1／R1，得到系統(tǒng)頻譜函數：

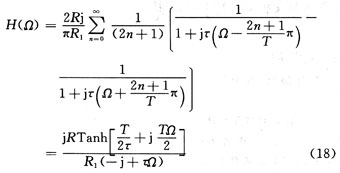
　　其中R／R1=τ／τ1，結果與式(14)一致，幅頻特性∣H(Ω)∣仍與式(11)相同。

　　4 結 語

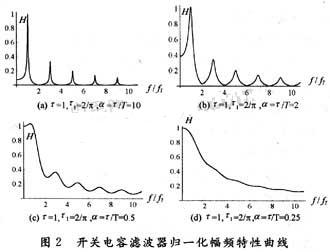
　　給定圖1(a)電路參數τ和τ1，選擇α=τ／T分別取不同值時，根據式(11)做出的歸一化幅頻特性曲線如圖2所示，結合對式(11)做深入分析表明：

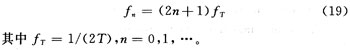
　　(1)α=τ／T較大時電路是梳齒幅度按奇數倒數規(guī)律衰減的梳狀濾波器，通帶中心頻率(梳齒)為：

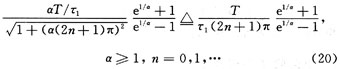
　　此時圖1(a)電路允許f=fT，f=3fT，f=5fT，…等頻率成份通過，且隨著頻率的升高，輸出幅度按奇數倒數規(guī)律逐漸減小。

　　(2)α=τ／T較大時，f=(2n)fT(其中n=0，1，2，…)是系統(tǒng)的阻帶中心頻率，落在這些頻點上的信號將獲得最小傳輸系數，最小傳輸系數(即梳狀濾波器幅頻曲線谷底高度)為：

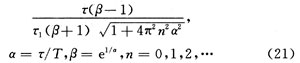
　　(3)該梳狀濾波器梳齒間隔(即阻帶中心頻率或通帶中心頻率間隔)為△f=2fT。

　　比較圖2可看出：開關轉換周期2T(相對于電路時間常數τ)越小，α越大，梳齒間谷底越接近零，梳齒越尖銳(即梳齒帶寬越窄)。例如，計算發(fā)現(xiàn)：圖2(a)中，α=τ／T=10，第一梳齒通帶寬度為B0.7=0.394fT。圖2(b)中，α=τ／T=2，第一梳齒通帶寬度為B0.7=2.33fT。

　　(4)隨著電子開關切換周期2T增大(α減小)，梳齒間谷底最小值逐漸增大。電路逐漸過渡為幅頻特性曲線輕微起伏的低通濾波器，如圖2(d)所示。低通濾波器傳輸函數極大值為：

　　由∣H(Ω)∣=0.707∣H(Ω)∣max可以求得低通濾波器上限截止頻率，結果表明，對于低通濾波器．仍為α越大，低通濾波器上限頻率(即帶寬)越小。