節能型循環泵控制器

　　2、永磁同步電機矢量控制系統

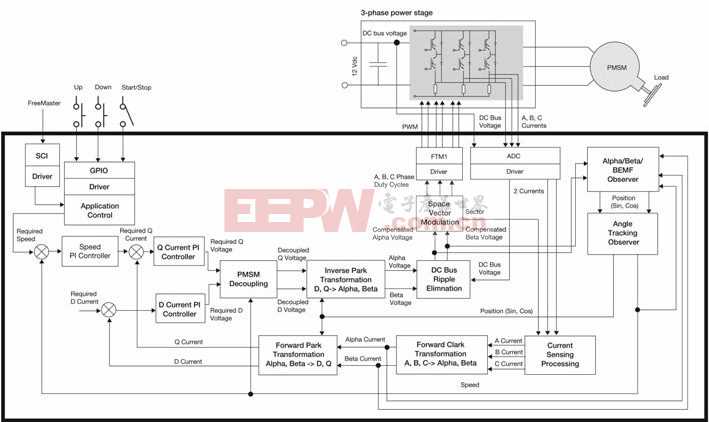
　　矢量控制理論于 1971 年由德國西門子公司的 F.Blaschke 提出。矢量控制的基本思想是將電機的三相電流經坐標變換變成以轉子磁場定向的兩相旋轉坐標系下，從而可以像直流電機那樣進行扭矩控制。矢量控制系統可在全速度范圍內實現電機電流的良好響應、控制效率高、調節器的設計比較容易實現、速度的調節范圍寬、具有良好的帶載起動性能。因此，矢量控制方案是PMSM 控制系統的首選方案。矢量控制算法的控制框圖如圖 2-1 所示：

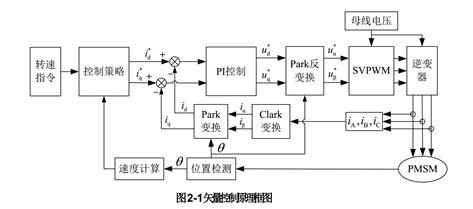
　　矢量控制的實現步驟如下：

　　1. 測量三相定子電流。可以只測量兩相電流，如

　　2. 檢測轉子位置和轉速，在無傳感器系統中使用 SMO 方法進行估計;

　　3. 將三相電流由三相靜止 ABC 坐標系變換到兩相靜止αβ 坐標系，得到

　　4. 將

　　5. 根據轉速指令和電機真實轉速進行 PI 運算，得到與扭矩控制直接相關的q 軸電流命令值

　　6. 根據dq軸電流的命令值和真實反饋值，得到相應的誤差電流，從而進行電流環 PI 運算，輸出結果為期望施加到電機上的電壓矢量

　　7. 將旋轉坐標系下的電壓矢量

　　8. 根據

　　下面詳細介紹各步驟的實現方法。

　　2.1 坐標變換

　　矢量控制的基礎是通過坐標變換將三相交流量變換到兩相直流量，從而可以使用經典的 PI 控制器加以控制。矢量控制中存在的坐標系主要包括：三相繞組對應的三相靜止 ABC 坐標系;兩相靜止αβ 坐標系;兩相旋轉dq坐標系。各坐標系的示意圖如圖 2-2 所示：

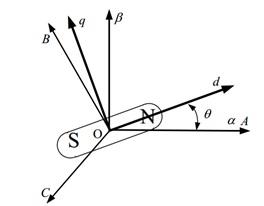
　　圖2-2 矢量控制中的 3種坐標系

　　2.1.1 Clark 變換

　　經 AD 測量得到的 3 相電流理論上是幅值相等、相位互差 120°的交流量，可以使用 Clark 變換將其變換到兩相靜止坐標系下。根據三相電流和為零可知，只需測量兩相電流即可完成此變換。Clark 變換公式如下：

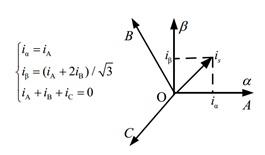
　　2.1.2 Park 變換

　　經過 Clark 變換后的電流信號仍然是交流量，不利于控制。因此使用 Park 變換將其變換到兩相旋轉坐標系下。進過 Park 變換后的電流信號變成了直流量。Park 變換公式如下：

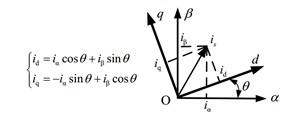
　　式中θ 為當前轉子位置。

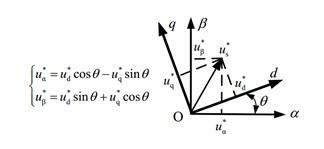
　　2.1.3 Park 逆變換

　　PI 調節器輸出的電壓 經過 Park 逆變換后才能得到 ，從而便于矢量調制。Park逆變換公式如下：

　　2.2 PI 控制器

　　PI 控制器用于對閉環控制中被控對象的誤差進行調節，輸出相應的控制量，以實現反饋值跟蹤命令值，從而得到期望的系統響應。PI 控制器結構簡單，易于數字化實現，因此被廣泛的應用于閉環控制系統中。

　　本文所設計到的電機控制系統中共存在 3 個相同結構的 PI 調節器，分別用于控制電機轉速、d 軸電流和q 軸電流。相應的 PI 控制器結構框圖如圖 2-3 所示：

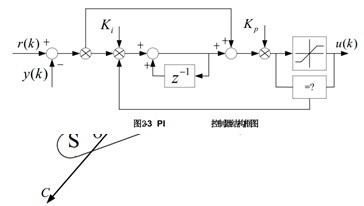
　　1) PI 控制器的比例增益Kp主要用于調節系統響應的快速性， Kp越大系統對誤差的響應越靈敏。但是過大的 Kp值會造成系統響應超調、穩態抖動等現象。

　　2) PI 控制器的比例增益Ki 主要用于調節系統響應的穩態精度。 Ki太小會降低系統的穩態精度; Ki太大會導致系統的穩態震蕩。

　　3) PI 控制器的限制積分飽和增益Kc 起到降低積分飽和對系統影響的作用。當系統的積分項發生飽和時，繼續增加積分項將不會影響輸出，此時輸出無法起到對系統的調節作用。 Kc用于限制積分飽和現象的發生，使得系統輸出從飽和狀態脫離出來。