基于FPGA的混沌加密虹膜識別系統設計(二)

　　是一個圓對稱函數，其平滑的作用可通過σ 來控制，由于對圖像進行線性平滑，數學上是進行卷積，令g(x，y)為平滑后的圖像，得到：

?

　　;

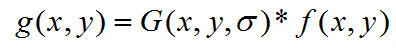
　　其中

?

　　是平滑前的圖像。

　　而沿梯度方向的二階導數是非線性的，計算較為復雜，Marr 提出用拉普拉斯算子來替代，即用

?

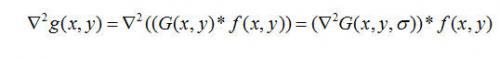
　　(7-14)

　　式中

?

　　為LOG(Laplacian of Guassian )濾波器。

?

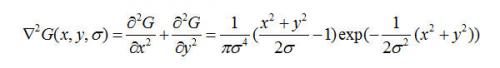
　　(7-15)

　　Marr 的

?

　　算子能較好地反映人們地視覺特性，通過對人眼視覺機理研究表明，對感受為同心圓的視神經細胞，其輸出相當于兩個高斯函數之差，視覺生理學中常用DOG(Difference of two Guassian functions)來描述：

?

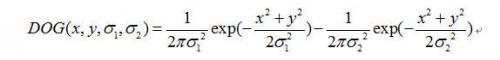
　　式中的正項代表激勵功能，負項代表抑制功能。

　　實驗表明，用不同的σ 高斯濾波器檢測邊緣，σ 越大，檢測到的邊緣越少，這一點可用濾波器的頻率特性說明：

　　由于高斯函數

?

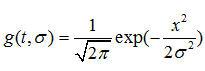
　　的傅立葉變換為：

?

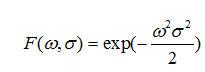
　　(7-16)

　　可見高斯平滑濾波器為低通濾波器，但σ 越大，頻帶越窄，對較高頻率的噪聲有很強的噪聲抑制作用。

　　為了可靠地檢測邊緣，有人同時用多個大小不同的尺度σ來進行濾波，這一點后來發展成為尺度濾波法。

　　7.3.3 利用邊緣檢測結果對圖像進行二值化

　　對于灰度值沒有變化的背景圖像，其一階二階導數

?

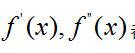
　　都為零，灰度值遞增，一階導數大于零，灰度值遞減，一階導數小于零。對于圖像的邊緣，往往是圖像灰度值激變的地方，其灰度的變化量達到峰值，即一階導數達到極值點，相對應二階導數為零，由數學分析中的函數理論可知，二階導數為正的點其灰度曲線是凹的，而二階導數為負的點其灰度曲線是凸的。對一幅灰度圖像來講，一旦灰度值發生變化，就可以從其二階導數上反映出來，二 階導數的正負可以反映灰度變化的形式。圖10顯示了一個函數及其二階導數的圖形。

　　設圖9為圖形中某一斑點的灰度截面圖，則按照下式就可以使圖像二值化，由背景圖案中顯示出此斑點。

?

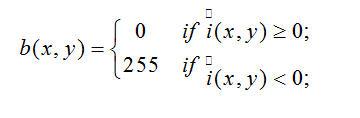
　　(7-17)

　　式中

?

　　為二值化的圖像，

?

　　為由(7-14)式進行高斯拉普拉斯變換后的圖像值，但是對于圖像截面的斑點，二值化后的圖像中卻顯示為一個圓環。對此，本文對式(7-17)做如下修正,以確保該點是一個斑點而不是一個圓環：若

?

　　大于等于零，則考察與它最近的非零點，若該點大于0，則其等于零，若該點小于零，則其等于255。在對圖像的掃描中，實際上是從左到右進行的，一種簡化的方法就是考察該已掃描的各點，由這些點中離該點最近的非零值來決定該點的值。因此二值化的表達式是：

?

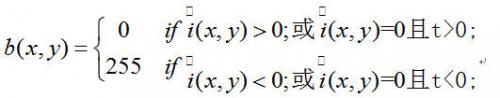
　　其中t 為圖像中(x，y)前方的最近的一個非零點，這樣改進以后可以減少特征點內部夾雜的斑點。

　　7.4 虹膜圖像比對及識別理論分析

　　有上述陳述我們知，歸一化后的虹膜圖像大小為720*50，這使得前期計算量較大。提取出720*50位的二值編碼后，在匹配時，用漢明距離(HD)對兩個虹膜特征碼進行匹配比對，公式如下：

?

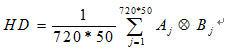
　　其中，

?

　　分別表示虹膜特征碼A和B的第j位編碼，

?

　　表示“異或”運算，當A和B對應的碼字相同時(都是1或者0)，則異或值為0;A和B對應的碼字不同時，則異或值為1。上式對兩個長度為720*50位的虹膜碼的對應每一位進行異或運算，如果兩個虹膜碼的每一位都相同，則HD=0;如果兩個虹膜碼的每一位都不同，則HD=1。因此，對于來自同一個虹膜的兩幅圖像來說，漢明距離比較小，對于來自不同虹膜的兩幅圖像來說，漢明距離比較大。

　　實際操作時，由于噪聲影響以及前面處理過程中不可避免地會引入誤差，來自于同一個虹膜的兩幅圖像的漢明距離不會是0，而是一個比較小的值;由于不同虹膜編碼的對應位相等和不等的概率是一樣的，因此，不同虹膜的兩幅圖像的漢明距離也不會是1，而是一個比較大的值。所以在匹配決策時，需要設定一個閾值，小于此閾值的兩幅圖像則認為屬于同一個虹膜，反之，則認為屬于不同的虹膜。

　　8.預期功能與目標

　　1)采集并識別虹膜圖像，實現身份認證。

　　2)在無按鍵喚醒的狀態下，系統暫停工作。

　　3)在工作狀態下，通過在PC上的實時展示圖像，進一步提高虹膜圖像的獲取質量。

　　4)在獲取分辨率的虹膜圖像的前提下，實現高精度的識別，將誤差降到最低。

　　5)在TFT上精確顯示比對結果，使得比對身份識別更加直觀。