基于DSP的實時數據無損壓縮實現方案

2 算法的選擇

無損壓縮就是對信源信息進行壓縮編碼后在解壓縮時能夠完全恢復，也即在壓縮和解壓縮過程中對信源信息沒有絲毫損失。常用的無損壓縮方法有Shannon- Fano編碼、Huffman編碼、游程(Run-length)編碼、LZW(Lempel-Ziv-Welch)編碼和算術編碼(ARC)等。對許多信息而言，沒必要完全保留全部特征。在允許一定精度損失的情況下，可以獲得更高的壓縮編碼效率。這類壓縮編碼方法成為有損壓縮。本設計采用無損壓縮，不再討論有損壓縮。

無損數據壓縮算法可以分為統計方法和詞典編碼方法。統計方法當以Huffman編碼和算術編碼(ARC)為代表。這種方法需要統計信源符號的概率分布情況，并根據統計結果產生壓縮碼。算術編碼是一種高效清除字串冗余的算法。仙儂信息論把字符aj出現的自信息量定義為I(aj)=-logpj I(aj)亦稱自信息函數，其含義實際是隨機變量X取值為aj時所攜帶信息的度量。自信息量的概率平均值，即隨機變量I(aj) 的數學期望值，稱做信息熵或簡稱熵。算術編碼從全序列出發，采用遞推形式連續編碼。它不是將單個的信源符號映射成一個碼字，而是將整個輸入符號序列映射為實數軸上[0，1)區間內的一個小區間，其長度等于該序列的概率，再在該小區間內選擇一個有代表性的二進制小數，而且是一個介于0和1之間的二進制小數作為實際的編碼輸出，從而達到了高效編碼的目的。例如算術編碼對某條信息的輸出為1010001111，它表示小數0.1010001111，也即十進制數 0.64。不論是否為二元信源，也不論數據的概率分布如何，其平均碼長均能逼近信源的熵。算術編碼的過程實際上也就是信源編碼試圖將任意的信息流與0、1 之間的間隔建立一一對應關系的過程。這樣要表示的信息流越長，則表示它的間隔就越小，用于表示這一間隔所需的二進制位就越多。

算術編碼在編碼前要求預先統計各信源符號概率，但無須排序，只要編、解碼端使用相同的符號順序即可。建立合理的信源概率模型是進行算術編碼的關鍵。信源概率模型的建立方法一般有兩種：一種是自適應的模型，是在不斷輸入信源的過程中對信源符號出現的概率進行統計，模型是在編碼過程中逐步建立起來并不斷更新；另一種是事先統計的模型，是在編碼前就對所有輸入信源符號的出現頻率進行事先統計，而編碼過程中模型不再改變。基于兩種模型算法的不同之處：事先統計模型在編碼之前就己經建立，編碼過程中不再更新，故壓縮效率與輸入字節數關系不大；而自適應模型是在編碼過程中建立并不斷更新，當輸入信源的數據量較大時，出現概率大的字符編碼位數較少的優越性才能得以體現。在復雜度上，由于后者需要不斷對模型進行更新，故運算量較大。

詞典編碼方法則是基于數據中許多結構頻繁重復再現這一事實，人們可以對相同符號串分配同一碼字、通過索引或者其他諸如此類的方法編碼。LZW算法可以在對數據統計特性一無所知的前提下，使壓縮率接近己知統計特性時所能夠達到的壓縮率，其運算速度快。LZW算法壓縮的原理在于用字典中詞條的編碼代替被壓縮數據中的字符串。字典中的詞條越長越多，壓縮率就越高。所以加大字典的容量可以提高壓縮率。但從字典中查找詞條是算法中最費時的工作，其字典的容量受到計算機內存限制，且字典也存在被填滿的可能。當字典不能再加入新詞條后，過老的字典就不能保證高的壓縮率。

不同的壓縮算法有不同的優點和缺點，不同算法的復雜性對空間的要求及壓縮率也不同。壓縮算法不僅僅依賴于壓縮方法本身，也依賴于被壓縮文本的特點。在本文中，由于是對實時數據的壓縮，對壓縮過程的時間性能要求高，所以采用事先統計模型的ARC。實驗證明，采用事先統計模型的ARC，其運算速度與LZW算法速度相近。而ARC算法在壓縮速度和壓縮去除率上都優于LZW算法。

3 實驗與結果

在比較字典編碼LZW與算術編碼ARC時，從壓縮速度和壓縮去除率上進行比較。前端以27Kb/s的速度實時采集8位的數據，數據壓縮后通過發送模塊以18Kb/s的速度數據傳到外界。對原始數據以2 048B作為分組長度考察其壓縮去除率及壓縮時間。

壓縮去除率＝(原始數據量－壓縮后數據量)/原始數據量

這是從空間角度衡量。實際上，對壓縮效率而言還必須關注其時間效率，本文采用“壓縮速度”的概念，定義如下：

壓縮速度＝原始數據量/壓縮所需要的時間以2 048B的數據分組進行分析：

1)從壓縮速度方面：完成2 048B的某噪聲數據，ARC算法需要5.64ms來完成，而LZW算法需要6.6ms，可見ARC算法的壓縮速度比較快。

(2)從壓縮效率方面：將某數據按照2 048B的長度進行分組并壓縮，從表1中可知ARC算法針對不同分組段的數據壓縮去除率恒定在78%左右，而LZW算法，在該分組段壓縮去除率僅為71%。可見該段數據ARC壓縮算法壓縮去除率比較高。

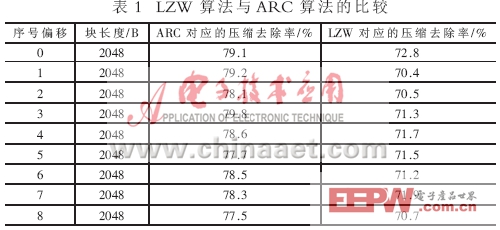
采用ARC算法后，通過大量的實驗數據的平均壓縮去除率為79%，滿足系統所要求的數據壓縮去除率大于50%的要求。用ARC算法壓縮2 048B的數據需要5.64ms左右。數據不同，壓縮時間會有所不同。通過對控制軟件讀取的數據進行解包、解壓，證明還原出來的數據與原始數據完全一致，實現了實時數據的無損壓縮。