基于比時法的晶振頻率測量建模與分析

　　3.2 晶振頻率誤差數(shù)據(jù)方差分析及顯著性檢驗

　　測量值y1，y2，…，yN之間的差異(稱為變差)是由兩方面的原因引起的。一是自變量取值的不同，二是其他因素(包括試驗誤差、隨機誤差等)的影響。為了對回歸方程進行檢驗，把兩者所引起的變差從y的總變差中分解出來。根據(jù)上述數(shù)據(jù)可得：

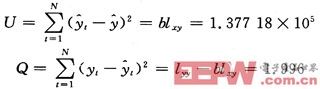
　　式中：U稱為回歸平方和，它反映了在y的總變差中由于x和y的線性關系而引起的y變化的部分；Q稱為殘余平方和，即所有測量點距回歸直線的殘余誤差平方和。

　　若總的平方和由N項組成，其自由度就為N-1，總的離差平方和的自由度可分為回歸平方和的自由度υU和殘余平方和的自由度υQ之和，即：

　　在一元線性回歸中，υU=1，υS=N-1，則Q的自由度υQ=N-2。由回歸平方和與殘余平方和的意義可知，一個回歸方程是否顯著，也就是y與x的線性關系是否密切，取決于U及Q的大小，U愈大Q愈小，說明y與x的線性關系愈密切。通常可以采用F檢驗法來對方程進行顯著性檢驗。對于一元線性回歸，將U及Q的值代入上式得到統(tǒng)計量F：

　　由F分布表可以查出，F(xiàn)≥F0.01(1，28)=7.64。可認為回歸是高度顯著的。

　　殘余平方和Q除以它的自由度υQ所得商：

　　稱為殘余方差，它可以看作排除了x對y的線性影響后，衡量y隨機波動大小的一個估計量。殘余方差的平方根：

　　稱為殘余標準差，它可用來衡量所有隨機因素對y一次性測量平均變差的大小，σ愈小，則回歸直線的精度愈高。

　　把平方和及自由度進行分解的方差分析數(shù)據(jù)結果歸納在一個表格中，如表3所示。

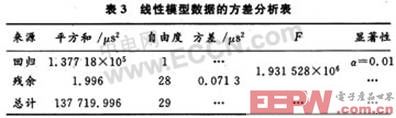
　　從表3可以看出，在30 s時間內(nèi)，晶振實際頻率與其標稱頻率的相對偏差引起的誤差平方和為1.377 18×105μs2，其他各種隨機因素引起的誤差的平方和為1.996μs2。晶振相對頻偏引起的誤差遠遠大于其他因素引起的誤差，表明了晶振頻率誤差貢獻主要來源于實際頻率與標稱頻率之間的頻偏。通過頻率修正即可得到一種高穩(wěn)定度的頻標源。

　　4 結語

　　以上分析結果表明，該晶振頻率誤差主要來源于實際頻率與標稱頻率的相對偏差，隨機誤差對晶振整體誤差的貢獻很小。通過對晶振標稱頻率值進行在線補償可以消除其相對頻偏，從而獲得一種具有較高穩(wěn)定度的頻率源，可為需要時間顯示的場所提供高精度的時間服務。