基于比時法的晶振頻率測量建模與分析
用最小二乘法們來估計參數(shù)β0,β。設(shè)b0,b分別是參數(shù)β0,β的最小二乘估計,于是得到一元線性回歸的回歸方程:
![]()
式中:b0,b是回歸方程的回歸系數(shù),分別表示晶振相對于標(biāo)準(zhǔn)頻率的初始誤差和累積誤差。應(yīng)用最小二乘法可求得回歸系數(shù)b,b0為:
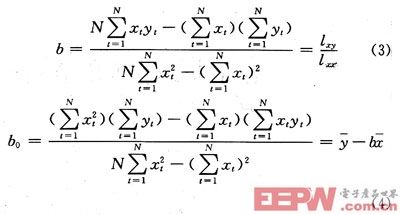
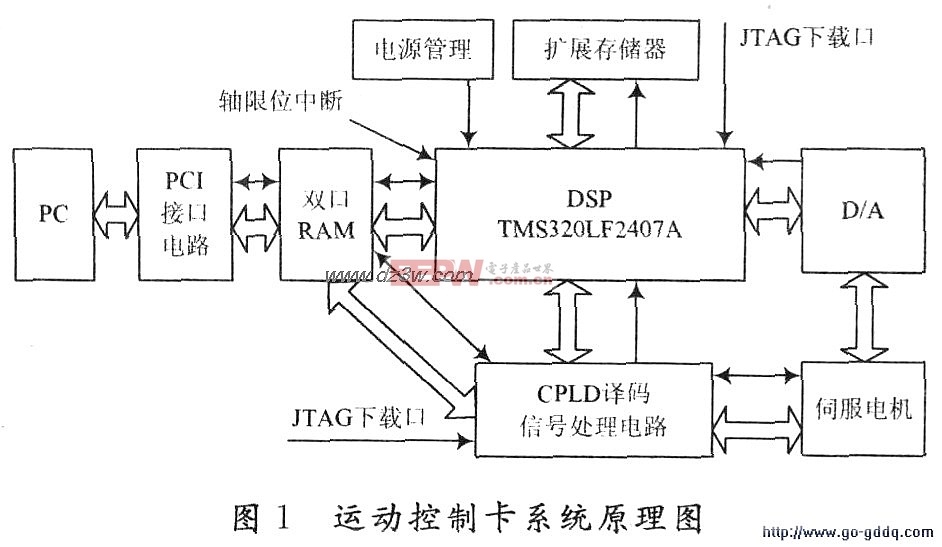
3 數(shù)據(jù)分析與處理
3.1 回歸系數(shù)估計
為了定量分析數(shù)據(jù),從而確定晶振頻率誤差的組成,首先對上述測得的數(shù)據(jù)進行歸一化處理。實際測量中得到的是晶振脈沖的計數(shù)個數(shù),設(shè)測量系統(tǒng)所用晶振頻率為10 MHz,可將計數(shù)數(shù)據(jù)轉(zhuǎn)化為晶振相對于標(biāo)準(zhǔn)時間每秒的時間之差。例如在x=30 s時,y=2 349,表示在第30 s時,晶振頻率相對于標(biāo)準(zhǔn)頻率的計數(shù)值為2 349,若晶振頻率f=10 MHz,則可得到在第30 s時晶振相對于GPS時間的誤差為t=y/f=234.9μs。
用Matlab對歸一化數(shù)據(jù)進行處理,依照最小二乘原理,得到計數(shù)時間x與時間差值y的均值,以及x的自相關(guān)、x和y的互相關(guān)、y的自相關(guān)及回歸方程如表2所示。


以上求得了回歸方程,但是該方程是否基本上符合y與x之間的客觀規(guī)律,是否符合晶振頻率誤差變化的實際特點,還需要對回歸方程做進一步的分析。在回歸分析法中,通常采用方差分析法們對回歸方程的顯著性進行檢驗,其實質(zhì)是將N個測量值的影響從數(shù)量上區(qū)分開,然后用F檢驗法對所求回歸方程進行顯著性檢驗。










評論