貝加萊機(jī)器人控制中的慣量前饋控制技術(shù)

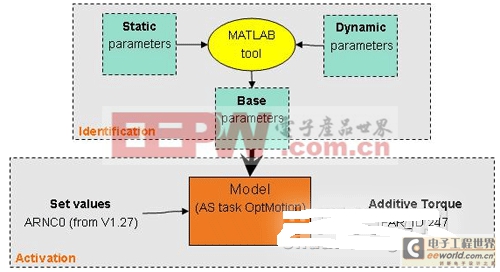
圖2 MATLAB/Simulink機(jī)器人運(yùn)動(dòng)仿真過(guò)程

機(jī)器人可表征為一個(gè)通過(guò)歐拉-拉格朗日方程建立的空間運(yùn)動(dòng)學(xué)方程，通過(guò)MATLAB，將系統(tǒng)的靜態(tài)參數(shù)，如機(jī)械臂長(zhǎng)度、質(zhì)量、關(guān)節(jié)減速比等及動(dòng)態(tài)參數(shù)，如旋轉(zhuǎn)角度、加速度、起始與終點(diǎn)位置等輸入到模型中，它提供了笛卡爾關(guān)節(jié)操作空間的動(dòng)力學(xué)模型，反應(yīng)了操作力與關(guān)節(jié)力之間的關(guān)系，操作空間與關(guān)節(jié)空間的速度與加速度關(guān)系，建立了關(guān)節(jié)輸入力矩與輸出力矩之間的關(guān)系。

這個(gè)模型是一個(gè)二次微分方程，可以通過(guò)歐拉-拉格朗日法進(jìn)行解析，可解析得出以下值：

慣量項(xiàng)；離心式和科里奧利項(xiàng)；引力項(xiàng)

當(dāng)建立模型后，我們可以進(jìn)行如下動(dòng)作：

1. 建立未知參數(shù)的識(shí)別

在系統(tǒng)中建立靜態(tài)參數(shù)、通過(guò)AS的力矩跟蹤來(lái)定義動(dòng)態(tài)參數(shù)的識(shí)別，并計(jì)算出基礎(chǔ)參數(shù)

2. 激活前饋控制

將所計(jì)算的基礎(chǔ)值輸出給BR PLC，通過(guò)AS軟件，在PLC中建立了一個(gè)運(yùn)動(dòng)模型，將這些基礎(chǔ)值給出后，系統(tǒng)將計(jì)算出一個(gè)附加力矩輸出值。

將該附加力矩輸出給驅(qū)動(dòng)器，驅(qū)動(dòng)器將在其電流環(huán)計(jì)算中，預(yù)先給出電流值，即可實(shí)現(xiàn)前饋控制，而這個(gè)附加值是通過(guò)系統(tǒng)不斷的計(jì)算，以微秒級(jí)的周期循環(huán)并提供給驅(qū)動(dòng)器的電流環(huán)計(jì)算的。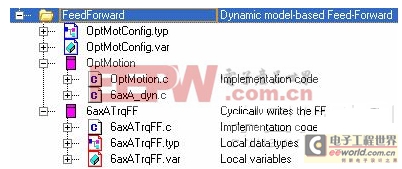

圖3 Automation Studio中的前饋控制程序

圖3為在Automation Studio中前饋控制的模型和，TrqFF為前饋周期寫(xiě)入，6AxATrqFF是采用C代碼寫(xiě)出的前饋實(shí)現(xiàn)代碼段。

五、控制效果

圖4是實(shí)際通過(guò)BR Automation Studio的軸監(jiān)測(cè)的示波器功能對(duì)整個(gè)輸出進(jìn)行采樣得到的扭矩控制過(guò)程變化曲線，其中藍(lán)色曲線為關(guān)閉前饋控制的情況，可以看到，其扭矩變化的波動(dòng)較大；而紅色曲線則表明了采用了前饋控制后的效果，明顯地提高了力矩輸出的穩(wěn)定性。

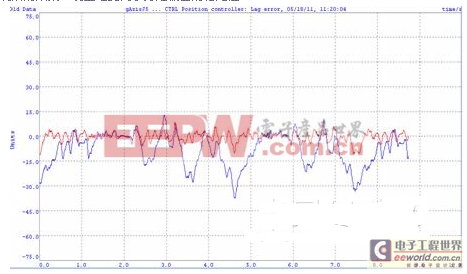
圖4 前饋控制效果

該項(xiàng)技術(shù)代表了機(jī)器人控制技術(shù)的最高水平，所設(shè)計(jì)的機(jī)器人系統(tǒng)其精度更高、運(yùn)行過(guò)程平穩(wěn)、抖動(dòng)較小，顯然優(yōu)于同類機(jī)器人系統(tǒng)的設(shè)計(jì)。