慣性變化時無刷直流電機的魯棒控制器設計
(2)干擾抑制性能:輸出速度(ωr)對負載干擾(tl)應該不敏感,即若參考輸入速度(ωr*)為0,當系統加上負載轉矩后,應有:
要滿足上式,則需選擇q使得的直流增益為0,即。由方程(13)可知,要滿足該條件,即有:
3.3 獨立參數的選擇
q的選擇必須滿足上述的約束條件以減小轉矩脈動,q一般具有以下形式:
 (15)
(15)式中a,b,pj均為自由設計參數,對系統的約束越多,則q的維數就越大,控制器就越復雜;反之,對系統的約束越少,則q的維數就越小,控制器就越簡單。
4 仿真結果及分析
電機參數為:
1/j=5(kg·m2)-1,b/j=0.002(sec)-1,kt=0.4v/(rad/s)
根據前面所述的控制器的設計過程,可以得到控制器k(s)為:
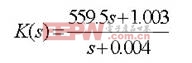
圖2記錄的是電機參數沒有變化時的轉速波形,從圖中可以看出,本文提出的控制器控制效果很好,轉速無波動,且調節時間很短,小于5ms。圖3記錄的是電機參數沒有變化時的負載干擾響應,從圖中可以看出,在很短的時間內,負載轉矩的影響就趨近于0。

圖2 標稱參數下的轉速響應
為了驗證在慣性參數大范圍變化情況下控制器的魯棒性,假設電機參數變為:
情況1 1/j=1(kg·m2)-1,b/j= 0.001(sec)-1
情況2 1/j=25(kg·m2)-1,b/j= 0.008(sec)-1
圖4、圖5分別為在標稱參數、參數變化(情況1)、參數變化(情況2)下的速度響應和負載干擾響應對比圖,由圖可以看出,即使電機慣性參數發生了很大的變化,系統依然穩定,各種動態性能仍然很好。
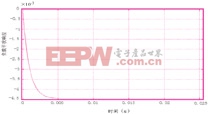
圖3 標稱參數下的負載干擾響應
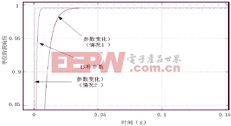
圖4 系統參數變化時的轉速響應
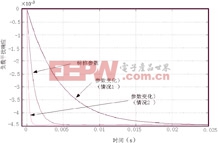
圖5 系統參數變化時的負載干擾響應
4 結束語
本文利用q-參數化理論設計了一個無刷直流電機魯棒控制器,用來減小由于各種原因導致的無刷直流電機的轉速波動。該控制器的主要特點是在電機由于運行時間和運行環境變化導致電機參數發生變化時,也能保證系統的魯棒穩定性和良好的動態響應,而且控制器階數很低。數字仿真結果驗證了該控制器的有效性。
作者簡介
姜偉東(1975-) 男 碩士,主要從事電力機車的檢修工作。
王勁松(1973-) 男 學士,主要從事工業自動化設計咨詢工作。
參考文獻
[1] 紀志成, 薛花, 董富紅. 無刷直流電機調速系統間接模型參考自適應控制[j].電機與控制學報, 2004,8⑶:225-228.
[2] 吳志瑜, 趙曉蓓, 劉愛軍等.無刷直流電動機位置伺服系統的變結構控制[j].微特電機,2006,34⑴:28-31.
[3] 趙學慶, 張國山, 陳學敏. 無刷直流電動機調速系統的模糊變結構控制[j].微特電機, 2006,34(7):20-22.
[4] m.azzam, yehia s.mohamed. robust controller design for automatic generation control based on q-parameterization[j]. energy conversion and management,2002, 43:1663-1673.
[5] abdelfatah m.mohamed, ilene busch-vishniac. imbalance compensation and automatic balancing in magnetic bearing systems using the q-parameterization theory[j]. ieee trans.on control system technology, 1995, 3⑵:202-211.
[6] abdelfatah m.mohamed,fumio matsumura, toru namerikawa et al. q-parameterization control of vibrations in a variable speed magnetic bearing[c]. proceedings of the 1997 ieee international conference on control applications. hartford, ct.october 5-7, 1997.
[7] selahattin ozcelik, howard kaufman. frequency domain design conditions for robust direct model reference adaptive controllers[c].proceedings of the american conference, albuquerque,new mexico june 1997.
[8] matt bement, suhada jayasuriya. synthesis of reduced order multivariable feedback tracking controllers using the q-parameterization[c]. proceedings of the 39th ieee conference on decision and control. sydney, australia,december, 2000.
[9] pragasen pillay, ramu krishnan. modeling, simulation, and analysis of permanent-magnet motor drives, part ii: the brushless dc motor drive[j].ieee trans.on industry applications,1989,25(2) 274-279.
[10]doyle j, francis b, and tannenbaum a. feedback control theory[m]. new york:macmillan publishing company.1992.本文引用地址:http://www.104case.com/article/236979.htm
pid控制相關文章:pid控制原理
pid控制器相關文章:pid控制器原理









評論