多傳感器模糊—概率交互作用的數(shù)據(jù)關(guān)聯(lián)算法
加入技術(shù)交流群
掃碼加入
和技術(shù)大咖面對(duì)面交流
海量資料庫(kù)查詢(xún)
在論域Zi(k)={Zij(k)}上，“某一量測(cè)可能來(lái)自目標(biāo)”所構(gòu)成的模糊集合Ai的關(guān)聯(lián)矩陣為(設(shè)目標(biāo)數(shù)為1)
μiA={μiA(Zij(k))}1×mk (5)
μiA(Zij(k))反映了目標(biāo)和第j個(gè)量測(cè)之間的模糊關(guān)聯(lián)度.于是，一旦得到一組量測(cè)，就查得到一組模糊信息Ai.由估計(jì)理論和模糊系統(tǒng)理論，可得到如下模糊最小方差估計(jì).
設(shè)參數(shù)集合X={X1,X2,…,Xm}為要估計(jì)的參數(shù).若所得到的估計(jì)量
ij使估計(jì)的均方誤差最小，則稱(chēng)ij為模糊最小方差估計(jì).
J=E{(Xj-ij)(Xj-ij)}=∫(Xj-ij).(Xj-ij)P(Xj|A)dXj (6)
ij應(yīng)使J達(dá)到極小.其中ij是基于模糊信息Ai對(duì)Xj的估計(jì)，它是Ai的函數(shù).令g(Ai)=ij.則
J=E{(Xj-g(Ai))T(Xj-g(Ai))} (7)
在上式中兩邊對(duì)g(Ai)求導(dǎo)，并令其為零，可得
ij=g(Ai)=E［Xj|Ai］=∫XjP(Xj|Ai)dXj (8)
為方便起見(jiàn)，略去下標(biāo)j,目標(biāo)在k時(shí)刻，第i個(gè)傳感器的狀態(tài)估計(jì)可以寫(xiě)成如下形式
i(k/k)=∫X(k)P(X(k)|Ai,Zi,k-1)dX(k) (9)
其中Zi,k-1={Zi(n)}k-1n=1表示第i個(gè)傳感器直到時(shí)刻k-1的累積量測(cè)集.式(9)的離散形式為
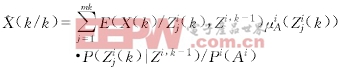(10)
(11)
令 Wij(k)=μiA(Zij(k))P(Zij(k)|Zi,k-1)/Pi(Ai) (12)
稱(chēng)Wij(k)為加權(quán)系數(shù).則式(10)可寫(xiě)為
(13)
假設(shè)X(k)是正態(tài)分布，則由Kalman濾波器得
評(píng)論