海量存儲機群系統中提高系統MTTF的設計和分析

下面，以m=3為例，求系統進入狀態m'的均值時間E3(T)。由一維生滅過程的瞬態分析，可得以下方程組。其中，Pi(t)表示在t時刻系統處于狀態i的概率。

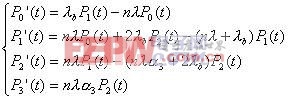
這是一個四元常系數線性微分方程組，可通過消元法消為一元線性微分方程，解之，然后可以求出其他各元的解。再根據邊界條件，可以求出各解中的系數。系統的邊界條件為

。 。

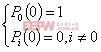而E3(T)可表示為：

。。

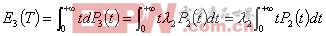為了求出E3(T)的具體值，還必須求出a3的值。限于篇幅，不加證明的給出如下求am的定理。

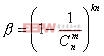定理：如果一個擁有n個節點的機群系統，含kn個互不相同的數據塊，每個數據塊都有m個備份，每個備份隨機地分布于機群系統中不同的節點上，那么當系統中出現有s-1個節點失效的時候，無數據塊丟失；而當系統中出現有s個節點失效的時候，系統中出現某個數據塊無法挽回地丟失的概率為， 其中， 并且s>=1。

根據此定理，求出當n=1000, m=3, k=100時a3=0.0006。

根據以上推導，可求出E3(T)在不同條件下的值，得到在n=1000, l=1/(24*3600) (/秒)的配置下，當lb=0.1(/秒)時，E3(T)=319天；當lb=0.05(/秒)時，E3(T)=86天；當lb=0.01(/秒)時，E3(T)=2天。類似地，可求出m=2時系統進入狀態m'的均值時間E2(T)，得到在n=1000, l=1/(24*3600) (/秒)的配置下，當lb=0.1(/秒)時，E2(T)=1.3小時；當lb=0.05(/秒)時，E2(T)=0.73小時；當lb=0.01(/秒)時，E2(T)=0.27小時。

分析以上數據可以得到兩個結論。第一，三個備份的系統比兩個備份的，能顯著地提升系統的MTTF。在通常配置下，三個備份的系統的MTTF可達幾十天；而兩個備份的系統的MTTF只能在1小時左右。第二，數據塊的轉移時間顯著地影響系統的MTTF，轉移時間越短，系統的MTTF越長。

4仿真實驗

下面，通過仿真實驗來驗證上面的結論。仿真實驗中的主要參數和限制條件如下。狀態塊總數與節點總數之比為rchunk=100，節點失效速率l=1/（24小時），節點恢復速率m=1/（24小時）。在進行狀態轉移時，源節點和目標節點的選擇策略：源節點，必須包含該狀態塊的備份，同時其上正在進行拷貝的狀態塊數目必須最小；目標節點，從所有不含該狀態塊的備份的節點中隨機選取，同時其上所存儲的狀態塊數目不能超過平均值的tcap=1.3。為保證狀態塊拷貝不影響系統的正常服務，人為限制正在進行拷貝的節點數目不超過機群系統中節點總數的tratio=40%。為了同樣的目的，人為限制狀態塊拷貝只占用網絡帶寬的一半；若有多個狀態塊在向外輸出，則它們分享帶寬。網絡帶寬為100Mb/s，一個狀態塊大小為64M。為了使新加入的節點不在短時間里收到大量的新備份，人為限制每個節點正在進行拷貝的狀態塊數目不超過tcopy=1。實驗結果，如圖2所表示。這些限制條件均來自實際系統。

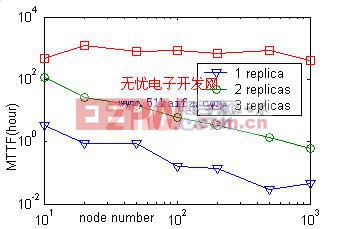
圖2不同備份數下的系統MTTF