量子處理器上大型多體哈密頓量的Krylov對角化

多體系統(tǒng)的低能量估計是計算量子科學的基石。變分量子算法可用于在容錯前量子處理器上準備基態(tài)，但它們?nèi)狈κ諗勘ＷC和不切實際的成本函數(shù)估計數(shù)量阻止了將實驗系統(tǒng)地擴展到大型系統(tǒng)。在預容錯設備上進行大規(guī)模實驗需要變分方法的替代方案。在這里，我們使用超導量子處理器在多達 56 個位點的二維晶格上計算量子多體系統(tǒng)的本能，使用 Krylov 量子對角化算法，該算法類似于著名的經(jīng)典對角化技術。我們使用在量子處理器上執(zhí)行的 Trotterized 酉進化來構建多體 Hilbert 空間的子空間，并在這些子空間內(nèi)經(jīng)典地對角化多體交互哈密頓量。這些實驗證明了對基態(tài)能量估計的指數(shù)收斂，并表明量子對角化算法已準備好在量子系統(tǒng)計算方法的基礎上補充其經(jīng)典算法。

介紹

求解量子多體系統(tǒng)的薛定諤方程是凝聚態(tài)物理學、量子化學和高能物理學等領域許多計算算法的核心。這項任務的量子優(yōu)勢將對自然科學產(chǎn)生深遠的影響。在使用量子計算機進行特征態(tài)計算的方法中，迄今為止有兩個主要討論對象：量子相位估計 （QPE）1,2，包括它最近的進展（例如，refs.3、4、5） 和變分量子特征求解器 （VQE）6.前容錯器件的實驗實現(xiàn)主要集中在 VQE 上，VQE 已在各種實驗平臺上針對各種問題（例如 refs.6、7、8、9).然而，到目前為止，參數(shù)優(yōu)化的瓶頸阻礙了它擴展到小型實例之外。另一方面，QPE 具有理論精度保證，但量子糾錯對于達到有價值問題所需的電路深度是必要的，盡管已經(jīng)實現(xiàn)了一些小例子10、11、12.

這些結果在迄今為止已經(jīng)執(zhí)行的小型演示與在容錯量子計算機上使用 QPE 或相關方法的大規(guī)模、高精度模擬之間留下了特征狀態(tài)估計方法的差距。在這項工作中，我們證明了 Krylov 量子對角化 （KQD）13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28，一種量子子空間對角化13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41，42，可以填補更普遍問題的空白。

KQD 的主要思想是使用量子計算機來近似地將哈密頓量投影到由初始參考狀態(tài)的各種時間演變跨越的 Krylov 空間中。然后將得到的低維矩陣進行經(jīng)典對角化，以獲得近似的低位能量特征態(tài)13.這種方法與 VQE 共享變分特性（最高可達噪聲的影響），但不需要迭代參數(shù)優(yōu)化，而是依賴于單輪電路執(zhí)行，然后進行經(jīng)典的后處理。此外，只要噪聲可以量化，該方法的準確性就可以在理論上受到限制27,28 元，這意味著 KQD 在過渡到容錯時代時可以繼續(xù)保持價值。在短期內(nèi)，對于現(xiàn)有的量子計算機來說，精度要求不那么嚴格的模擬的時間演變并不是令人望而卻步的。雖然在這種情況下量化所有誤差源的影響可能具有挑戰(zhàn)性，但 KQD 仍然作為一個啟發(fā)式方法，具有潛在的指數(shù)收斂，朝向基態(tài)能量的噪聲估計。

在這項工作中，我們使用 KQD 來估計海森堡模型在重六邊形晶格上的基態(tài)能量。我們表明，盡管噪聲對高精度構成了重大障礙，但即使使用高級錯誤緩解功能也是如此43,44 元，我們可以在多達 56 個量子比特上獲得到基態(tài)能量的收斂。

結果克雷洛夫量子對角化理論

KQD 包括兩個主要步驟。第一個是構造矩陣的量子子例程

$${tilde{H}}_{jk}=langle {psi }_{j}|H|{psi }_{k}rangle，qquad {tilde{S}}_{jk}=langle {psi }_{j}|{psi }_{k}rangle，$$(1)

它對應于哈密頓量投影到子空間 （{{mathcal{K}}}={{rm{Span}}}{leftvert {psi }_{0}rightrangle，ldots，leftvert {psi }_{D-1}rightrangle }）的重疊（Gram）矩陣。第二步是經(jīng)典求解投影到子空間中的與時間無關的薛定諤方程，該方程由下式給出

$$tilde{H}c=Etilde{S}c，$$(2)

其中 c 是 Krylov 空間中的坐標向量。在整個希爾伯特空間或對稱扇區(qū)內(nèi)的近似基態(tài)能量為 （2） 的最低特征值。兩個不同的分量會影響近似的精度27,28 元：將完整特征值問題向下投影到子空間的內(nèi)在誤差，這與足夠低能量的狀態(tài)與子空間的重疊有關，以及任何其他算法、統(tǒng)計和硬件錯誤。

子空間對角化方法的主要區(qū)別在于子空間的選擇。在經(jīng)典計算中，一種常見的方法是通過局部運算符（例如費米子的跳躍項）生成相關性來構造子空間，就像在多引用配置交互中一樣45.或者，可以使用全局運算符。例如，經(jīng)典的 Lanczos 方法采用哈密頓量的冪級數(shù)來構造子空間 （{{{mathcal{K}}}}_{P}={{rm{Span}}}{{H}^{，j}leftvert {psi }_{0}rightrangle }），也稱為冪或多項式 Krylov 空間。這種結構的主要優(yōu)點是，解的精度隨著子空間大小 D 的出現(xiàn)呈指數(shù)級提高46,47,48 元.經(jīng)典 Lanczos 和相關方法的限制因素是，由于需要表示糾纏量子態(tài)，它們不可避免地會受到內(nèi)存消耗的影響，內(nèi)存消耗會隨著系統(tǒng)大小呈指數(shù)級增長。

雖然已經(jīng)提出了這種方案對量子計算機的各種改編13,14,15,16,17,18,21,22,23,24,25,26,27,28,29,30,31,32,35,36,37,38,39,40,41,42，最適合近期量子計算機的是使用實時演化作為全局算子來生成 Krylov 空間：

$${{{mathcal{K}}}}_{U}={{rm{Span}}}{{U}^{， j}leftvert {psi }_{0}rightrangle }，quad j=0,1，ldots，D-1，$$(3)

其中 U = e?iH dt是某個時間步 dt 的時間演化算子13,14,15,16,17,18,21,22,23,24,25,26,27,28.這樣做的優(yōu)點是雙重的：首先，時間演化可以通過足夠短的深度電路來近似，以便在現(xiàn)有量子設備上實現(xiàn)。其次，可以證明，即使在存在噪聲的情況下，投影到這個酉 Krylov 空間引起的誤差也會與 Krylov 維度呈指數(shù)級快速收斂，就像在經(jīng)典的 Krylov 算法中一樣。噪聲只是貢獻一個額外的誤差項，只要它不是太大以至于完全壓倒信號27,28 元.這意味著有可能達到近似基態(tài)能量與有限維的 Krylov 空間的收斂。

雖然在量子計算機上評估 Krylov 矩陣解決了內(nèi)存問題，這是經(jīng)典方面擴展的主要障礙，但量子方面的主要障礙是噪聲。兩個主要貢獻是有限散粒采樣導致的統(tǒng)計噪聲和器件中的硬件噪聲。來自時間演變近似的算法誤差也進入了，但下面我們用數(shù)字表明它的影響低于硬件誤差的水平。另一方面，為了擴大模擬的規(guī)模，抑制和減輕這些硬件錯誤被證明是至關重要的：我們?yōu)榇四康膽昧藢嶒灱夹g（詳見補充說明 4），同時保持量子電路盡可能淺，同時保持 Krylov 空間的全局耦合結構。

為了簡化我們的電路，我們利用了許多凝聚態(tài)模型所具有的 U（1） 對稱性，包括我們關注的海森堡模型。作為量子比特運算符，U（1） 對稱性可以表示為漢明權重守恒;就 spin-1/2 算子而言，它對應于總自旋的 z 分量守恒。等效地，我們可以將對稱子空間視為 k 粒子子空間，將 ↑（↓） 自旋視為粒子的不存在（存在）。

圖 1 顯示了原則上可用于計算矩陣元件的電路序列 （1）。面板 （a） 顯示了標準 Hadamard 檢驗，這將是此類計算的默認工具。圖 （b） 說明了我們?nèi)绾问褂米孕睾銇肀苊鈱崿F(xiàn)傳統(tǒng) Hadamard 測試中存在的受控時間演化：相反，我們實現(xiàn)了參考狀態(tài) （leftvert {psi }_{0}rightrangle） 的受控初始化，然后依賴于時間演化保持“真空態(tài)”（leftvert 00ldots 0rightrangle） 直到經(jīng)典可計算階段的事實。

圖 1：Krylov 量子對角化示意圖。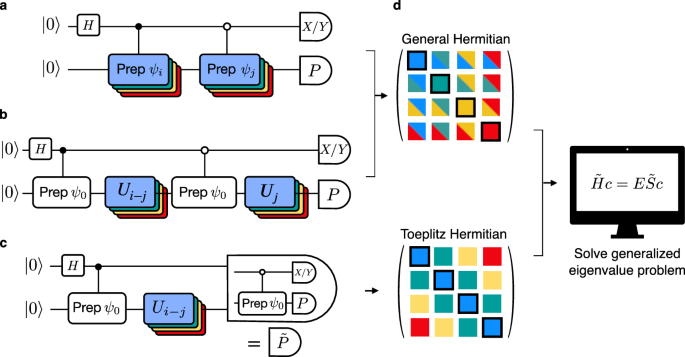

用于計算 〈 形式的矩陣元素的 Hadamard 電路ψ我∣P∣ψj〉，它依賴于 Krylov 基態(tài)的受控單一實現(xiàn)。b 通過利用對稱性（如粒子數(shù)守恒）來簡化電路。c 這項工作中采用的結構。只需要一個時間演進電路，第二個受控制備電路被吸收到測量的基礎上。d 經(jīng)典后處理構造矩陣 （tilde{H}） 和 （tilde{S}），這會產(chǎn)生一個廣義特征值問題。矩陣對于 a、b 中所示的電路是 Hermitian，對于 c，它們是 Toeplitz Hermitian。請注意，由黑線括起來的對角線元素可以經(jīng)典地計算。

作為第二個簡化，我們注意到對于確切的時間演變，（langle {psi }_{0}|{U}_{j}^{{dagger} }H{U}_{k}|{psi }_{0}rangle=langle {psi }_{0}|H{U}_{k-j}|{psi }_{0}rangle） 中，它為我們提供了兩種形式上等效的方法來測量相同的矩陣元素，第二種方法產(chǎn)生了更簡單的電路，因為它只涉及一次時間演化。然而，一旦時間演變通過 Trotterization 近似化，這兩個表達式就不再相等。在圖 .1c，我們顯示了與后一個版本相對應的電路。

目前尚不清楚人們是否應該更喜歡圖 b 或 c 中所示的電路。1，純粹從 Trotter 錯誤的角度來看。圖 .1b 是它仍然對應于子空間中的變分優(yōu)化，因為每個矩陣元素仍然具有 （1） 形式。然而，在存在有限樣本和器件噪聲的情況下，即使如此28.圖 1c 是顯式強制執(zhí)行 Toeplitz 結構的版本，從電路深度的角度來看更可取，原因有兩個：它只需要一次演化，因此，第二次受控初始化可以作為 Clifford 變換應用于哈密頓量中的 Pauli 可觀察對象，而不是在電路中顯式實現(xiàn)。在實踐中，由于使用了正則化技術來避免特征值問題 （2） 的不良調(diào)節(jié)，我們沒有看到這種方法對變分的顯著破壞（詳見補充注釋 5）。例如，我們比較了圖 1 中電路的精確經(jīng)典仿真結果。1b、c，它們將在實驗中編譯，如圖 1 所示。2 （有關詳細信息，請參閱下一節(jié)）。圖 20 量子比特系統(tǒng)的能量曲線。3 表示變分隨著 Trotter 步數(shù)的增加而迅速恢復。這些發(fā)現(xiàn)使用圖 1 中所示的電路版本進行激勵。1c.

圖 2：Krylov 量子對角化的量子電路。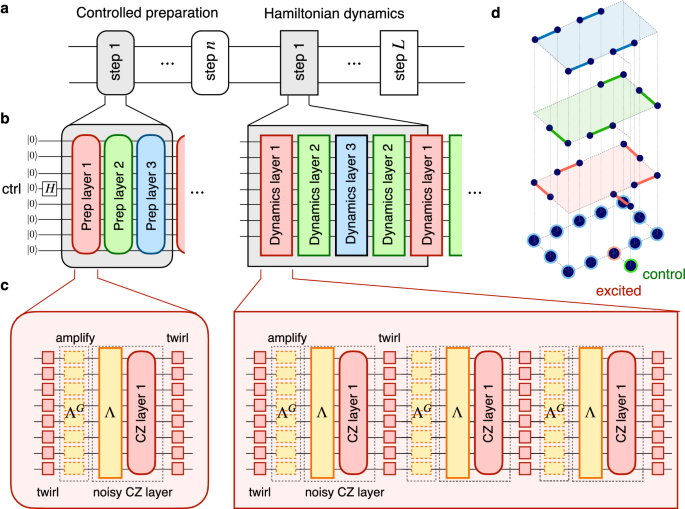

a 每個回路在目標粒子扇區(qū)內(nèi)執(zhí)行初始狀態(tài)的受控準備，然后是 Trotterized 時間演化。b 受控制備準備一個計算基態(tài)，其中漢明權重對應于給定實驗的粒子數(shù)，在輔助量子比特上進行控制。由于重六邊形晶格可以是邊緣三色的（圖中顏色由紅色、綠色和藍色表示），因此可以使用三個獨特的雙量子比特門層的序列來實現(xiàn)受控準備和 Trotterized 時間演化，這些層與單量子比特旋轉交錯。有關詳細信息，請參閱正文。c 每層雙量子比特門都經(jīng)過 Pauli 旋轉，以便根據(jù)稀疏 Pauli-Lindblad 噪聲模型 Λ 定制噪聲43,44 元，前面是其擴增 ΛG對于 PEA。請注意，源自源電路、旋轉層或噪聲放大層的單量子比特門的相鄰層始終組合在單個層中;為了清楚起見，它們未合并到圖中。CZ 層的 d （12 + 1） 量子比特示例。

圖 3： 算法誤差的數(shù)值研究。

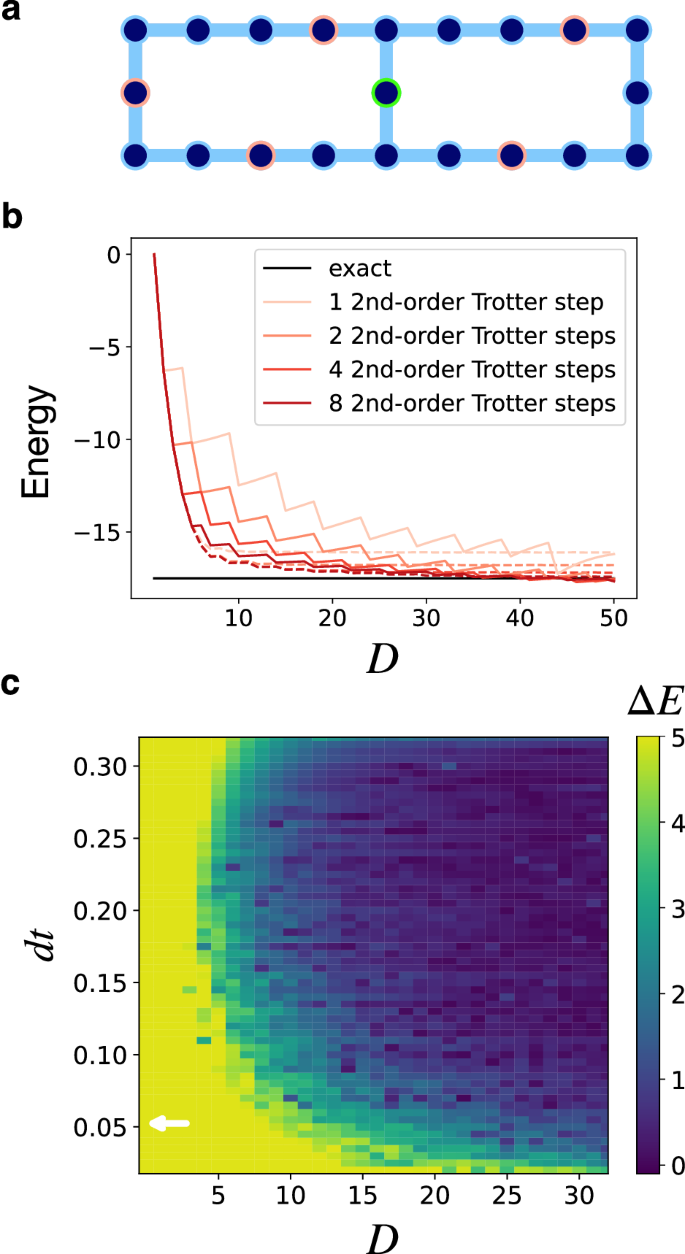
用于數(shù)值模擬的海森堡模型的 （20 + 1） 量子比特布局，綠色和紅色圓圈表示控制和激發(fā)量子比特。b 能量與克雷洛夫空間維度。虛線和實線表示圖 1 中電路的結果。1b、c 分別。c 使用 4 個二階 Trotter 步驟，k = 5 粒子扇區(qū)具有不同 dt 和 D 的基態(tài)能量誤差 ΔE 的熱圖。白色箭頭表示 π/||H||.

大型實驗演示

在我們的實驗中，我們研究了自旋 1/2 反鐵磁海森堡模型，該模型將一組邊 E 定義為

$$H={sum}_{（i，j）in E}{J}_{ij}（{X}_{i}{X}_{j}+{Y}_{i}{Y}_{j}+{Z}_{i}{Z}_{j}）$$(4)

帶均勻聯(lián)軸器 J我J= 1，其中 X我、 Y我、 Z我表示第 i個站點上的 Pauli 矩陣。相互作用集 E 是重六邊形晶格的子集（見圖 D）。4）. 請注意，雖然重六邊形晶格是二分的，因此可以使用路徑積分蒙特卡洛方法有效地模擬整個希爾伯特空間中的基態(tài)49，符號問題通常存在于激發(fā)態(tài)中。在激發(fā)態(tài)中，我們關注幾個 k 粒子子空間中能量最低的特征態(tài)。k 粒子子空間的維度為 O（Nk).請注意，電路構造依賴于 U（1） 對稱性，而不是 SU（2） 對稱性，因此我們的方法也直接適用于 XXZ 模型。

圖 4：多體哈密頓量的實驗對角化。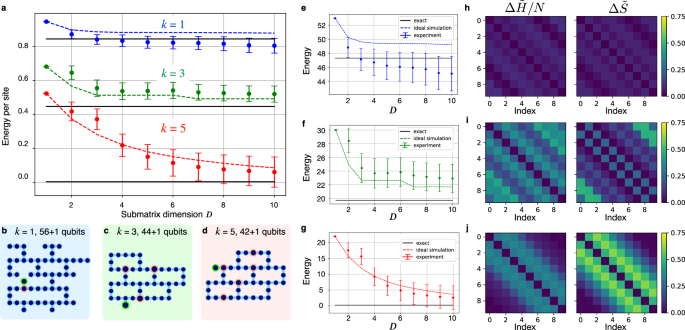

a 在系統(tǒng)大小分別為 N = 56、44 和 42 的情況下，粒子數(shù) k = 1、3 和 5 的海森堡模型的每位點能量。誤差線表示通過 bootstrap 估計的標準差。虛線表示無噪聲經(jīng)典模擬的能量，黑色實線表示給定 k 粒子子空間中的確切最低能量。b–d 量子比特布局圖。綠色和紅色圓圈分別表示粒子的控制和初始位置。例如，單個粒子數(shù) k = 1、3 和 5 的能量曲線。h–j 誤差矩陣 （Delta tilde{H}/N ：=|{tilde{H}}_{exp }-{tilde{H}}_{{{rm{num}}}}|/N） 和 （Delta tilde{S} ：=|{tilde{S}}_{exp }-{tilde{S}}_{{{rm{num}}}}|），其中下標 “exp” 和 “num” 分別表示來自實驗和數(shù)值計算的數(shù)據(jù)

我們在三個不同的 k 粒子扇區(qū)中運行了實驗：k = 1、3、5。所有三種情況下的初始狀態(tài)都是計算基態(tài)，其數(shù)字為 （leftvert 1rightrangle） s，由 k 給出：例如，在單粒子情況下，（leftvert {psi }_{0}rightrangle=leftvert 00ldots 1ldots 0rightrangle）。因此，k的不同值的電路實現(xiàn)在受控準備中有所不同（見圖）。1 和 2）。k = 1 情況對應于在初始狀態(tài)下僅生成一個粒子，這可以通過控制量子比特（Hadamard 測試中的輔助）和相鄰量子比特之間的 CX 門輕松實現(xiàn)。對于 k > 1，我們?yōu)榱Ｗ舆x擇了大致均勻分布在量子比特圖上的位置。

重六邊形晶格允許對其邊緣進行三種著色，其中每種顏色對應于一層可以同時實現(xiàn)的雙量子比特門（見圖 D）。2）. 由于每個不同的雙量子比特層都需要自己的噪聲學習以進行概率誤差放大 （PEA—見下文），因此最大限度地減少電路中不同層的數(shù)量是有利的。受控準備電路可以使用一組雙量子比特層來實現(xiàn)，這些層對應于重六邊形中邊緣的三種顏色，與任意層相比，開銷是恒定的（有關詳細信息，請參見補充說明 2）。對于我們的 Trotterized 時間演化，我們將哈密頓項劃分為同一組層。因此，對于每個實驗，我們只需要學習總共三個獨特層的噪聲模型。

電路的受控初始化部分的深度與量子比特圖中兩個相距最遠的初始粒子之間的距離成正比。我們使用兩個二階 Trotter 步驟來近似我們所有實驗中的時間演變。具有三個哈密頓項交換組的 r 二階 Trotter 步驟需要 4 個r +1 個雙量子比特層（參見圖 b 中的面板 b）。2），在我們的例子中，電路的時間演化部分產(chǎn)生了 9 層。

為了測量對應于 （tilde{H}） 和 （tilde{S}） 中矩陣元素的實部或虛部的可觀察量，我們將可觀察量劃分為盡可能少的局部交換集（測量基數(shù)），因為這些集合是可共同測量的7.縮短的電路，如圖 3 的第三行所示。1，需要第二個受控初始化電路共軛哈密頓項 （4），因為它沒有物理實現(xiàn)。這產(chǎn)生了相同數(shù)量的 Pauli 可觀察對象，因為受控初始化是一個 Clifford 電路，并且可以證明這些可觀察對象可以劃分為 2（k + 2） 個測量基;見補充說明 2。

我們在 Heron R1 處理器IBM_montecarlo上進行了實驗。這是一個 133 量子比特設備，具有固定頻率的 transmon 量子比特，通過可調(diào)諧耦合器相互連接。與前幾代固定耦合器件相比，Heron 處理器具有更快的雙量子比特門（持續(xù)時間與單量子比特門相似）和更低的串擾。為了進一步改進測量的可觀察對象（參見圖 .1），我們使用了概率誤差放大 （PEA）44和旋轉讀出誤差消除 （TREX）50，以減少 SPAM 錯誤，以近似無噪聲期望值。我們還采用了錯誤抑制，特別是 Pauli 旋轉和動態(tài)解耦。增補說明 4 中提供了錯誤緩解和抑制的詳細信息。

在我們的實驗中，對于每個測量基礎，生成了一定數(shù)量的旋轉實例，然后針對不同的噪聲放大因子值重復測量每個實例。對于單粒子 （k = 1） 實驗，我們使用了 300 個旋轉實例，每個實例 500 次拍攝，噪聲放大系數(shù)為 1、1.5、3。對于 k = 3、5，我們使用了 100 個旋轉實例，每個實例有 500 次拍攝，噪聲系數(shù)為 1、1.3、1.6。為較大的實驗引入減少旋轉實例是為了減少總運行時間，因為測量堿基的數(shù)量以及電路大小隨著 k 的增加而增加。噪聲放大因子的調(diào)整是由于較深電路中的噪聲率增加。電路的受控初始化部分涉及創(chuàng)建控制量子比特的最大糾纏狀態(tài)和初始粒子位置。隨著粒子數(shù)量的增加，這轉化為在電路開始時準備的更大的最大糾纏狀態(tài)，這反過來又使結果更容易受到噪聲的影響。

在所有實驗中，Krylov 空間的大小固定為 D = 10，以便在設備重新校準過程的時間尺度 （24 h） 內(nèi)實現(xiàn)算法的總運行時間。對于固定值 k ，實驗在特定的量子比特子集上運行，該子集根據(jù)設備的當前狀態(tài)使用啟發(fā)式例程進行選擇，以實現(xiàn)最佳量子比特映射51.k = 1 實驗在 57 量子比特子集上執(zhí)行，k = 3 實驗在 45 量子比特子集上執(zhí)行，k = 5 實驗在 43 量子比特子集上執(zhí)行（布局如圖 4 所示）。4）. 后兩個部分是手工選擇的，以便在每種情況下有五個完整的重六角形。

盡管時間步長 dt 理論上具有 π/||H||27,28 元，則對低粒子數(shù)子空間的限制會改變這一點。因此，我們啟發(fā)式地選擇了時間步長，k = 1、3 和 5 的值分別為 0.5、0.022 和 0.1。

結果如圖 1 所示。4. 圖 a 在歸一化能量尺度上總結了結果，而 e、f 和 g 顯示了每個單獨實驗的收斂曲線。相應的量子比特圖分別顯示在面板 b、c 和 d 中。這些收斂曲線是評估噪聲 KQD 實驗結果的有用診斷工具。我們從理論分析中了解到，如果誤差率足夠低，可以解析信號，即區(qū)分 Krylov 空間中的最低能量狀態(tài)和純噪聲，那么我們應該看到能量向與真實基態(tài)能量偏移一個常數(shù)的值呈指數(shù)衰減，具體取決于誤差率27,28 元.我們的結果表明，這種行為在一定程度上會有所波動，這是意料之中的，因為理論結果只提供了指數(shù)衰減的上限。然而，如果噪聲完全主導了信號，那么相對于系統(tǒng)大小，與子空間維度的收斂速率將呈指數(shù)級緩慢，因此我們不會在圖 1 中看到最初的快速收斂。4. 有關更多詳細信息，請參閱補充說明 4 和 5。

在我們的實驗結果中，噪聲和算法誤差（由于 Trotter 近似以及有限的 Krylov 維數(shù)）仍然是重要的限制因素，最準確的估計能量（D = 10 時）與真實值之間的差異證明了這一點。我們使用自舉法估計了實驗能量的標準差，因為求解正則化、廣義特征值問題 （2） 的后處理使直接誤差傳播變得困難。這產(chǎn)生了圖 1 中的誤差線。4;有關更多詳細信息，請參閱補充說明 5。圖 4 還顯示了我們電路的理想經(jīng)典仿真的能量收斂曲線，這些曲線可以通過僅在受限粒子數(shù)子空間中表示向量和運算符來實現(xiàn)。雖然由于實驗結果的噪聲導致誤差線很大，但我們對兩個較大 k 值的估計能量與幾乎所有點的這些標準差的理想模擬曲線一致。

在 k = 1 實驗中，結果偏離于真正的最低能量，表明噪聲已經(jīng)從 k = 1 子空間產(chǎn)生了有效的泄漏。這說明了依賴對稱守恒來保留在特定子空間中的風險，盡管研究全局基態(tài)不會受到這種擔憂。

精確對角化也可以在本實驗中研究的 Hilbert 空間扇區(qū)中進行，但不能在整個 Hilbert 空間中進行。然而，除了受控初始化的電路深度減小外，實驗并未以任何方式依賴于那些特定的粒子數(shù)扇區(qū)，因此縮放沒有定性或結構障礙，只有噪聲的影響。在我們關注的特定情況下，海森堡模型在二維重六邊形晶格上的基態(tài)，仍然可以使用張量網(wǎng)絡等經(jīng)典技術計算精確的近似值。

有人可能會問，為什么使用 KQD 而不是最近為近期或早期容錯設置中的基態(tài)能量估計而開發(fā)的其他各種算法之一，例如，3、4、5、52.一個主要原因，除了 KQD 相對廣為人知的噪聲容忍度21,25,27,28 元，這些替代方法都從時間演化中提取特征能，而不是直接從哈密頓量本身的投影中提取特征能。在我們這樣的環(huán)境中，這是一個問題，其中 Trotter 電路隨著時間步長數(shù)量的增加而保持固定（這對于最小化電路深度是必要的），因為 Trotter 電路的頻譜與理想時間演變的頻譜不同，實際上變得周期性，周期取決于時間步長和固定的 Trotter 電路。因此，在這種約束下，隨著時間步數(shù)的增加，僅依賴于演化的算法將在某個時候停止收斂。

討論

這里介紹的 KQD 方法豐富了在前容錯量子處理器上進行基態(tài)估計的量子算法的前景，填補了 VQE 和 QPE 之間的空白。一種稱為基于樣本的量子對角化 （SQD） 的互補子空間算法，基于采樣和復雜的經(jīng)典后處理，使用以量子為中心的超級計算 （QCSC） 架構53最近被用于演示超越蠻力解決方案的化學量子模擬。這種 QCSC 方法產(chǎn)生經(jīng)典可驗證的能量，并且不需要近似時間演化，這使得它在短期內(nèi)對于包含大量項（例如分子哈密頓量）的哈密頓量來說很容易處理。對于凝聚態(tài)應用，KQD 具有可證明的收斂保證，給定具有逆多項式重疊的初始參考狀態(tài)，并且其電路在預容錯處理器上是可行的，如本工作所示。

為了將這項工作的規(guī)模與先前的基態(tài)能量實驗量子模擬進行比較，可以基于量子比特計數(shù)或基于使用的希爾伯特空間維度進行比較。兩者都是相關的，因為，例如，即使我們的單粒子實驗的子空間只有 56 維，它也會產(chǎn)生 57 量子比特量子電路的誤差。我們最大的子空間維度是 5 粒子實驗，其子空間維度為 850668，介于 19 和 20 個量子比特的完整希爾伯特空間維度之間。我們在表 1 中展示了用于基態(tài)能量模擬的端到端量子算法的最大（據(jù)我們所知）先前的實驗演示，并通過上述兩個指標進行評估。請注意，我們只包括實現(xiàn)整個算法的實驗，而不是例如，經(jīng)典地優(yōu)化 VQE 的參數(shù)，然后只在量子計算機上估計單個能量。

1. QC-QMC 是指混合量子-經(jīng)典量子蒙特卡洛算法。

如表 1 所示，我們的實驗在量子比特方面比以前的工作高出兩倍多，在希爾伯特空間維度上比以前高出兩個數(shù)量級以上，但 ref 除外。53，它與上一段討論的適用范圍完全不同。人們可能還會注意到，這些實驗所達到的精度差異很大，但正如我們的重點是如上所述，在規(guī)模上實現(xiàn)收斂，而規(guī)模的增加使我們的工作與小規(guī)模實驗（包括一些未在表 1 中所示的實驗）處于不同的狀態(tài)，后者實現(xiàn)了更高的準確性。換句話說，這項工作代表了基態(tài)能量量子模擬技術的最新進展。