利用史密斯圓圖設計T和Pi匹配網(wǎng)絡
通過使用史密斯圓圖設計T和Pi匹配網(wǎng)絡,了解更多關于L形截面和阻抗匹配的信息。
本文引用地址:http://www.104case.com/article/202412/465595.htm阻抗匹配網(wǎng)絡是射頻電路的核心部分。通過將負載阻抗轉換為所需值,我們可以確保滿足某些性能條件,如最大功率傳輸。
在上一篇文章中,我們看到稱為L形截面的雙元件集總網(wǎng)絡可用于在特定頻率下提供阻抗匹配。雖然L段被廣泛使用,但它們并沒有給我們選擇帶寬的靈活性。對于給定的輸入和輸出阻抗,這些電路的帶寬是恒定的。考慮到這一點,在許多應用中,我們通常需要控制匹配網(wǎng)絡的帶寬。當需要比L段更窄的帶寬時,應該采用更復雜的布置,如T或Pi網(wǎng)絡。
本文使用史密斯圓圖深入討論了這些類形的匹配網(wǎng)絡的設計。史密斯圓圖是電氣工程師菲利普·哈格·史密斯的發(fā)明。
史密斯圓圖常數(shù)Q圓
在深入討論之前,熟悉史密斯圓圖上的恒定Q圈是很重要的。之前,我們將阻抗Z=R+jX的電路節(jié)點的節(jié)點Q定義為:
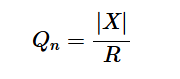
我們還討論了最大Qn指定了L形截面的品質因數(shù),從而指定了帶寬。對于史密斯圓圖,我們更喜歡使用歸一化阻抗z=r+jx。即使使用歸一化阻抗,我們仍然可以使用上述方程,因為分子和分母都除以相同的歸一化因子。因此,我們得到方程式1:
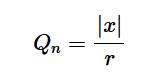
方程式1
史密斯圓圖上有無數(shù)個點產(chǎn)生相同的Qn。例如,點z1=0.2+j0.2、z2=0.5+j0.5、z3=1+j和z4=2+j2都對應于Qn=1。Qn=1的常數(shù)Q曲線如圖1中的史密斯圓圖所示。
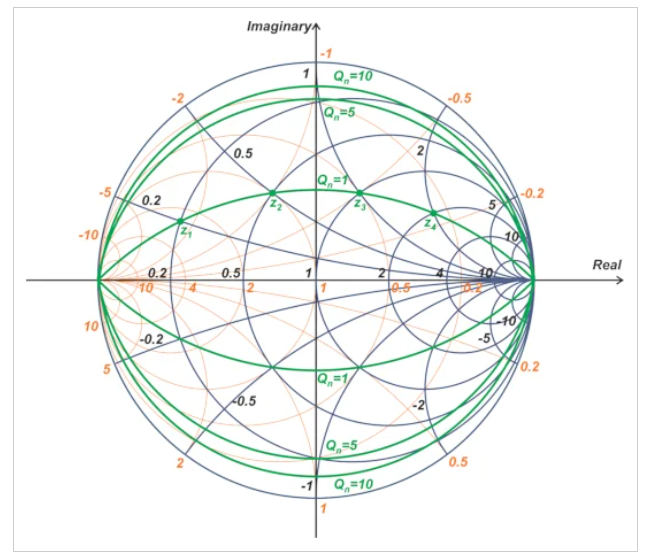
圖1 史密斯圓圖顯示Qn=1的常數(shù)Q曲線
根據(jù)方程式1,z1、z2、z3和z4的復共軛也產(chǎn)生Qn=1。這些點也對應于史密斯圓圖下半部分的另一條Qn=1曲線。此外,上圖顯示了Qn=5和10的恒定Q輪廓。可以證明,Qn=a的阻抗在Γ平面上變換為兩個圓。兩個圓都有半徑
√1+1a21+1a2,,一個中心位于(0,-1/a),另一個中心在(0,1/a)。有關這方面的更多信息,我建議閱讀Guillermo Gonzalez的《微波晶體管放大器:分析與設計》一書。
T形匹配網(wǎng)絡的基本思想
我們將通過一個例子來解釋這種方法。考慮將zLoad=0.2變換到史密斯圓圖的中心。這種阻抗變換的一種選擇是使用與下圖所示的青色路徑相對應的兩元件匹配網(wǎng)絡(圖2)。
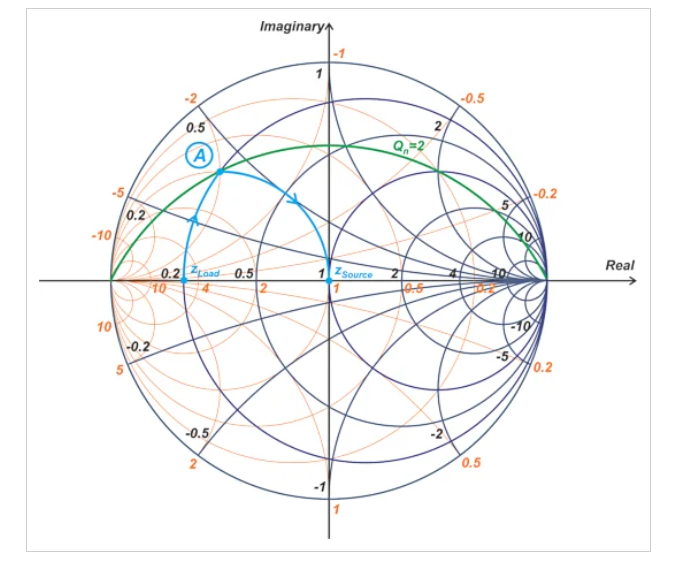
圖2 史密斯圓圖顯示了使用與青色路徑(a)對應的二元匹配網(wǎng)絡的阻抗變換
由于只允許兩個運動從zLoad到zSource,因此中間阻抗必須位于r=0.2和g=1圓的交點處(圖中的點A)。這意味著,對于二元網(wǎng)絡,我們無法調整中間阻抗的位置,因此電路的品質因數(shù)是固定的。正如我們所看到的,在我們的例子中,交點位于Qn=2的圓上。您可能想知道,如果我們繼續(xù)沿著r=0.2的圓運動到點A上方的某個點,會發(fā)生什么。如圖3所示。
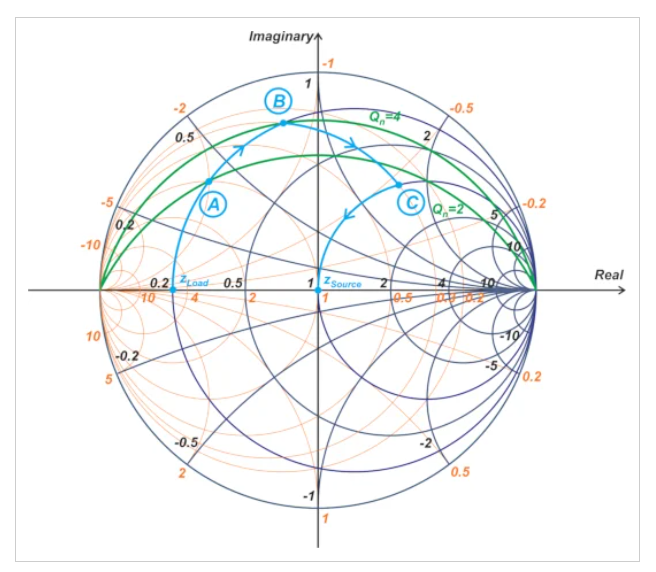
圖3 史密斯圓圖顯示r=0.2的圓
在上面的例子中,我們移動到點B而不是點A,得到Qn為4。然而,我們現(xiàn)在需要至少兩個額外的運動才能從B點移動到圖表的中心。第一個運動沿著g=0.3的恒定電導圓,第二個運動沿著r=1的恒定電阻圓。上圖所示的路徑需要兩個串聯(lián)組件和一個并聯(lián)組件,從而形成一個T形匹配網(wǎng)絡,如圖4所示。
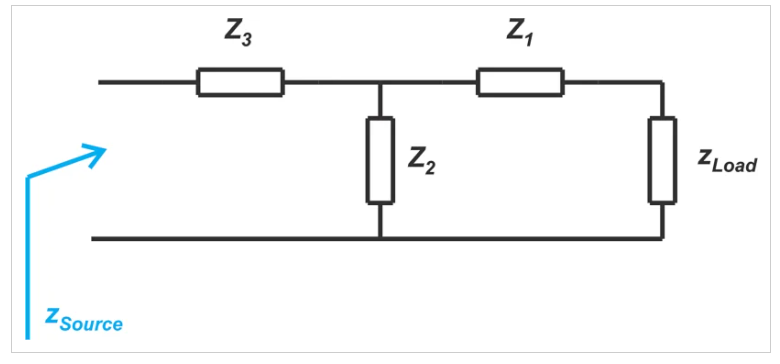
圖4 使用兩個串聯(lián)和一個并聯(lián)組件創(chuàng)建T形匹配網(wǎng)絡
上述電路允許我們將最大節(jié)點Q從2增加到4,但代價是使用三元件匹配網(wǎng)絡。參考更完整的史密斯圓圖,我們現(xiàn)在可以找到上述阻抗匹配解決方案的中間點a、B和C的電抗和電納。表1提供了這些信息。

表1 A、B和C點的電抗和電納
讓我們找到元件值,并比較這兩個電路的頻率響應
查找元件值、響應和帶寬
下面我們將向您展示如何找到L形截面和T形網(wǎng)絡的元件值,以及這些匹配網(wǎng)絡技術的頻率響應和帶寬。
查找L形截面元件值
假設歸一化阻抗為Z0=50Ω,感興趣的頻率為1 GHz。L形截面的分量值如下。從zLoad到點A的運動對應于一個串聯(lián)電感器,其歸一化電抗為xA-xLoad=j0.4-j0=j0.4。這需要1 GHz的3.18 nH串聯(lián)電感器。
圖2中從A點到zSource的運動需要一個并聯(lián)電容器,其電納為bSource-bA=0j-(-j2)=j2。這可以通過6.37pF并聯(lián)電容器產(chǎn)生。最后的L形截面如圖5所示。
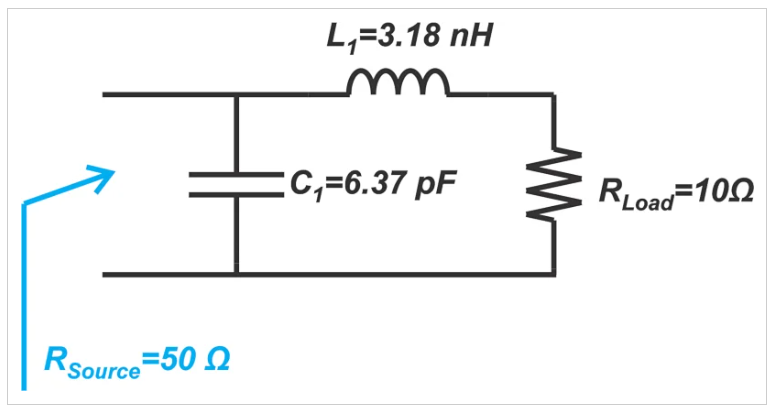
圖5 示例L形截面圖
查找T形網(wǎng)絡元件值
接下來,我們可以以類似的方式找到T形網(wǎng)絡的分量值。在這種情況下,從zLoad到點B的運動對應于6.37nH電感器產(chǎn)生的歸一化電抗為j0.8的串聯(lián)電感器。下一個運動需要bC-bB=-j0.47-(-j1.2)=j0.73的電容電納,這可以通過2.32 pF的電容器獲得。最后,我們需要一個電抗為j1.53的串聯(lián)電容器才能到達圖表的中心,這可以通過2.08 pF的電容器來實現(xiàn)。最終的T形網(wǎng)絡如圖6所示。
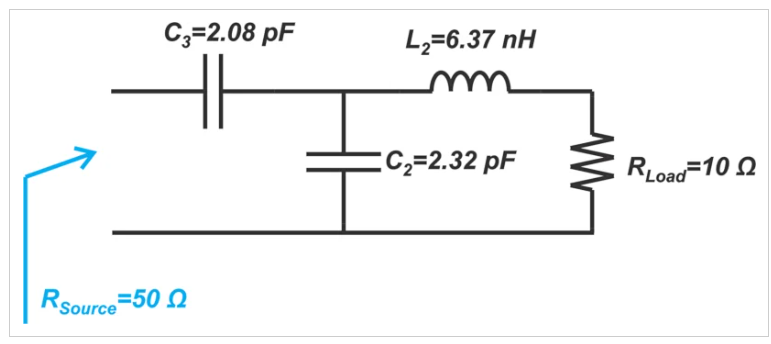
圖6 示例T形網(wǎng)絡圖
L段和T形網(wǎng)絡頻率響應和帶寬
這兩個電路的頻率響應如圖7所示。
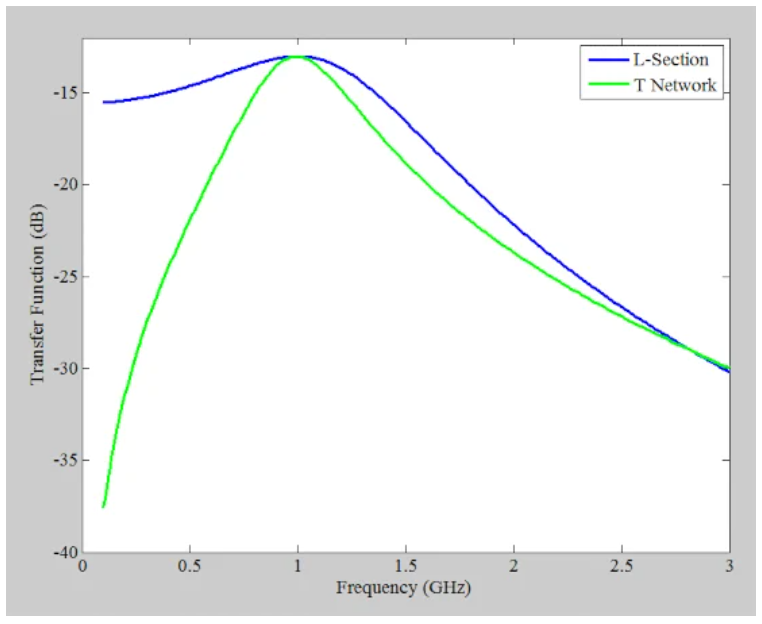
圖7 T形網(wǎng)絡和L形截面頻率響應
L形截面具有低通響應,其上限3dB截止頻率為1.46 GHz。在1 GHz以下,電路沒有3 dB的截止頻率。這是由于電路的Q值低。如果我們假設響應在1 GHz左右是對稱的,我們可以將帶寬近似為21.46-1=0.92 GHz。
讓我們使用上一篇文章中的知識來驗證這個值。我們知道L形截面的品質因數(shù)QL是其最大節(jié)點Q(Qn)的一半。從圖2中,我們得到Qn=2,因此QL=1。因此,帶寬應為:
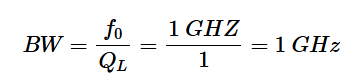
該方程與模擬結果基本一致。另一方面,對于T形網(wǎng)絡,上限和下限3dB點分別位于1.29 GHz和750 MHz,導致帶寬為540 MHz。正如我們所看到的,T形網(wǎng)絡允許我們增加電路的節(jié)點Q,并實現(xiàn)比L形截面更低的帶寬。在T形網(wǎng)絡中將Qn與QL精確地聯(lián)系起來并不簡單(Pi網(wǎng)絡也是如此,我們稍后會介紹)。然而,T或Pi網(wǎng)絡的Q通常被視為電路中Qn的最高值。
我們可以通過T形網(wǎng)絡減少Qn嗎?
上述討論表明,T形網(wǎng)絡可以產(chǎn)生比L形截面更大的Qn。現(xiàn)在出現(xiàn)的問題是,我們能否使用T形網(wǎng)絡將Qn降低到L形截面以下?要回答這個問題,請考慮圖8中的史密斯圓圖。
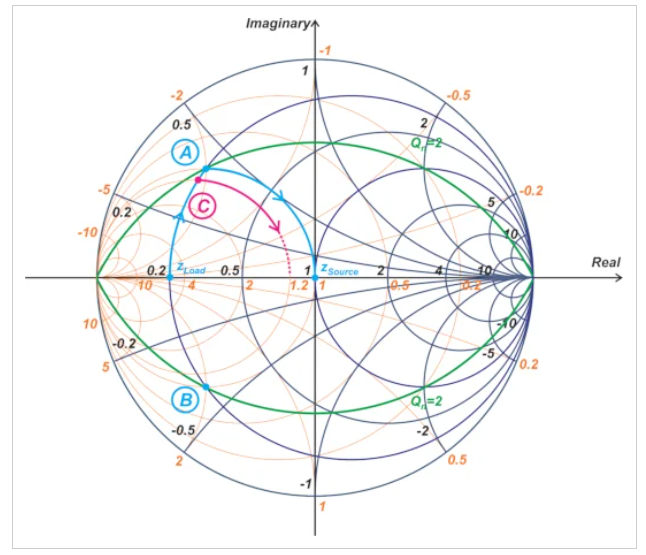
圖8 史密斯圓圖,點C處有中間阻抗
在上圖中,我們選擇了Qn小于2的點C處的中間阻抗。由于我們的目標是有一個T形網(wǎng)絡,我們應該繼續(xù)沿著穿過點C的恒電導圓運動(在我們的例子中g=1.2圓)。要有一個三元網(wǎng)絡,g=1.2的圓必須與穿過zSource的r=1的圓相交。然而,上圖顯示,如果中間點C的Qn小于2,則穿過C的恒定電導圓不會與r=1的圓相交。因此,不可能有Qn小于L形截面的T形網(wǎng)絡。
Pi匹配網(wǎng)絡的設計
另一種類形的三元素匹配網(wǎng)絡是下面描述的Pi網(wǎng)絡(圖9)。
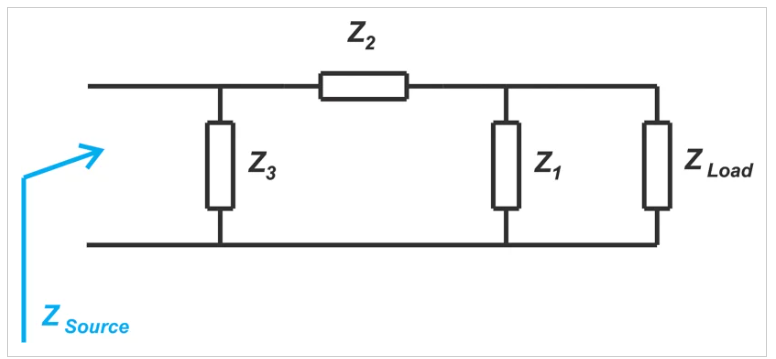
圖9 Pi網(wǎng)絡圖示例
讓我們設計一個Pi網(wǎng)絡,將zLoad=3.33轉換為1 GHz史密斯圓圖的中心。假設最大Qn被要求為4。對于Pi電路,ZLoad和ZSource旁邊的元件是并聯(lián)元件,因此,我們可以沿著穿過源和負載阻抗的恒定電導圓移動。這些恒電導圓和Qn=4曲線的交點可以用作中間點,如圖10所示。
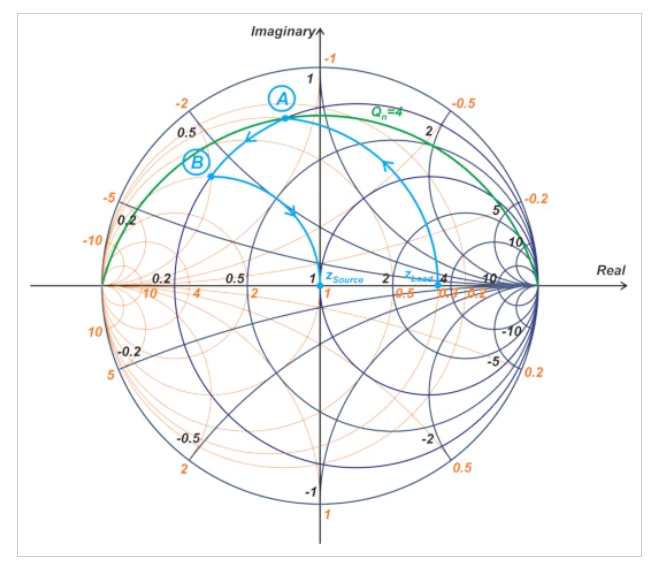
圖10 史密斯圓圖顯示了恒定電導圓和作為中間點的Qn=4曲線
在這個例子中,g=0.3的圓是通過zLoad的恒定電導圓。此圓與Qn=4曲線的交點(上面的點A)用作阻抗變換的中間點。下一步應該是沿著穿過點A的恒定電阻圓(這對應于Pi網(wǎng)絡的串聯(lián)分量)。在我們的例子中,r=0.2圓是穿過點A的恒定電阻圓。r=0.2圓和g=1恒定電導圓的交點是我們的下一個中間阻抗(點B)。最后,我們沿著g=1的圓移動,到達史密斯圓圖的中心。使用更完整的史密斯圓圖,我們可以找到點a和b的電抗(x)和電納(b),如表2所示。

表2 A點和B點的電抗和電納
中間點
使用這些信息,我們可以找到元件值。從zLoad到點A的運動需要-j1.2的歸一化電納,這可以通過1 GHz的6.63 nH并聯(lián)電感器來實現(xiàn)(假設Z0=50Ω)。從A點到B點的運動需要j0.4-j0.8=-j0.4的歸一化電抗,這可以通過7.96 pF串聯(lián)電容器獲得。最后,從B到zSource的運動需要j2的歸一化電納,從而產(chǎn)生6.37pF的并聯(lián)電容器。最終電路如圖11所示。
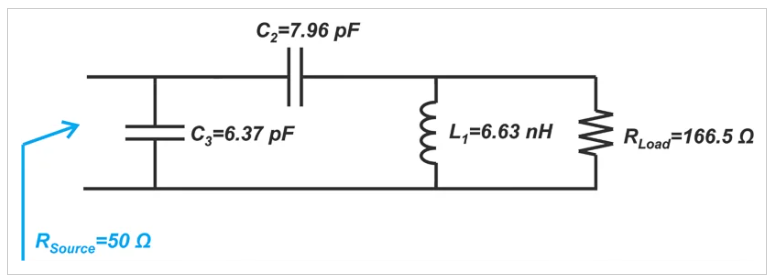
圖11 Pi網(wǎng)絡示意圖
電路的頻率響應如下圖所示。
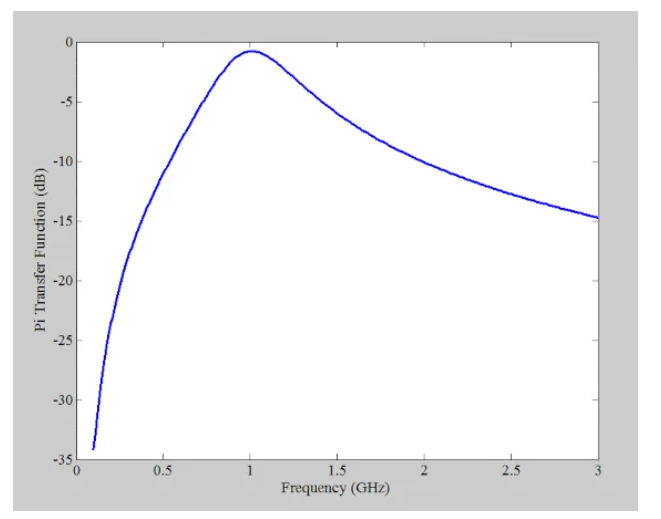
圖12 Pi網(wǎng)絡頻率響應
對于Pi網(wǎng)絡,上3dB點和下3dB點分別位于1.3 GHz和780 MHz,帶寬約為520 MHz。
使用T和Pi匹配網(wǎng)絡概述
雖然L段是非常實用的電路,但它們并沒有給我們選擇帶寬的靈活性。對于給定的輸入和輸出阻抗,這些電路的帶寬是恒定的。當需要比L段更窄的帶寬時,可以采用更復雜的布置,如T或Pi網(wǎng)絡。請記住,這些類形的網(wǎng)絡只能提高電路的品質因數(shù)(或等效地降低帶寬)。在下一篇文章中,我們將研究可以提供比簡單L段更寬帶寬的匹配電路。



評論