如何使用LTspice對復雜電路的統計容差分析進行建模

摘要

LTspice^?可用于對復雜電路進行統計容差分析。本文介紹在LTspice中使用蒙特卡羅和高斯分布進行容差分析和最差情況分析的方法。為了證實該方法的有效性，我們在LTspice中對電壓調節示例電路進行建模，通過內部基準電壓和反饋電阻演示蒙特卡羅和高斯分布技術。然后，將得出的仿真結果與最差情況分析仿真結果進行比較。其中包括4個附錄。附錄A提供了有關微調基準電壓源分布的見解。附錄B提供了LTspice中的高斯分布分析。附錄C提供了LTspice定義的蒙特卡羅分布的圖形視圖。附錄D提供關于編輯LTspice原理圖和提取仿真數據的說明。

本文介紹可以使用LTspice進行的統計分析。這不是對6-sigma設計原則、中心極限定理或蒙特卡羅采樣的回顧。

公差分析

在系統設計中，為了保證設計成功，必須考慮參數容差約束。有一種常用方法是使用最差情況分析(WCA)，在進行這種分析時，將所有參數都調整到最大容差限值。在最差情況分析中，會分析系統的性能，以確定最差情況的結果是否在系統設計規格范圍內。最差情況分析的效力有一些局限性，例如：

■   最差情況分析要求確定哪些參數需要取最大值，哪些需要取最小值，以得出真實的最差情況的結果。

■   最差情況分析的結果往往會違反設計規范要求，致使必需選擇價格高昂的元件才能得到可接受的結果。

■   從統計學來說，最差情況分析的結果不能代表常規觀察到的結果；要研究展示最差情況分析性能的系統，可能需要使用大量的被測系統。

進行系統容差分析的另一種替代方法是使用統計工具來進行元件容差分析。統計分析的優點在于：得出的數據的分布能夠反映出在物理系統中通常需要測量哪些參數。在本文中，我們使用LTspice來仿真電路性能，利用蒙特卡羅和高斯分布來體現參數容差變化，并將其與最差情況分析仿真進行比較。

除了提到的關于最差情況分析的一些問題外，最差情況分析和統計分析都能提供與系統設計相關的寶貴見解。關于如何在使用LTspice時使用最差情況分析的教程，請參見Gabino Alonso和Joseph Spencer撰寫的文章“LTspice: 利用最少的仿真運行進行最差情況的電路分析”。

蒙特卡羅分布

圖1顯示在LTspice中建模的基準電壓，使用蒙特卡羅分布。標稱電壓源為1.25 V，公差為1.5%。蒙特卡羅分布在1.5%的容差范圍內，定義251個電壓狀態。圖2顯示251個值的直方圖，圖中包含50個條形區間(bin)。表1表示與該分布相關的統計結果。

圖1 電壓源的LTspice原理圖（使用蒙特卡羅分布）

圖2 1.25 V基準電壓的蒙特卡羅仿真結果，以50個條形區間和251個點組成的直方圖呈現

表1 蒙特卡羅仿真結果的統計分析

高斯分布

圖3顯示在LTspice中建模的基準電壓，使用高斯分布。標稱電壓源為1.25 V，容差為1.5%。蒙特卡羅分布在1.5%的容差范圍內，定義251個電壓狀態。圖4顯示251個值的直方圖，圖中包含50個條形區間(bin)。表2表示與該分布相關的統計結果。

圖3 電壓源的LTspice原理圖（使用3-sigma高斯分布）

表2 高斯參考仿真結果的統計分析

圖4 1.25 V基準電壓的3-sigma高斯仿真結果，以50個條形區間和251個點組成的直方圖呈現

高斯分布是以鐘形曲線表示的正態分布，其概率密度如圖5所示。

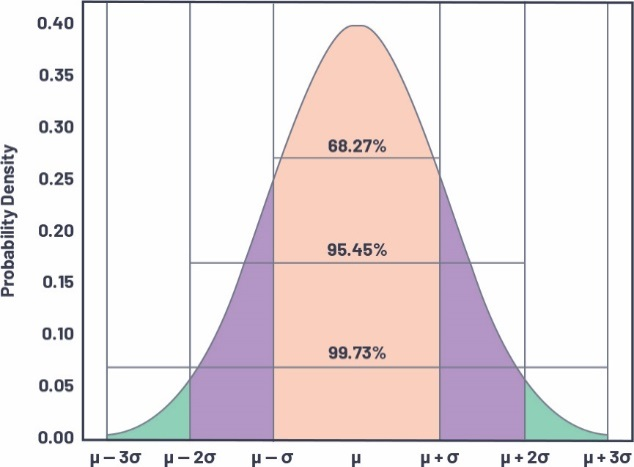
圖5 3-sigma高斯正態分布

理想分布和LTspice仿真的高斯分布之間的關聯如表3所示。

表3 LTspice仿真的251個點高斯分布的統計分布

綜上所述，LTspice可用于仿真電壓源的高斯或蒙特卡羅容差分布。該電壓源可用于對DC-DC轉換器中的基準電壓進行建模。LTspice高斯分布仿真結果與預測的概率密度分布高度吻合。

DC-DC轉換器仿真的容差分析

圖6顯示DC-DC轉換器的LTspice仿真原理圖，使用壓控電壓源來模擬閉環電壓反饋。反饋電阻R2和R3的標稱值為16.4 kΩ和10 kΩ。內部基準電壓的標稱值為1.25 V。在該電路中，標稱調節電壓VOUT或設定點電壓為3.3 V。

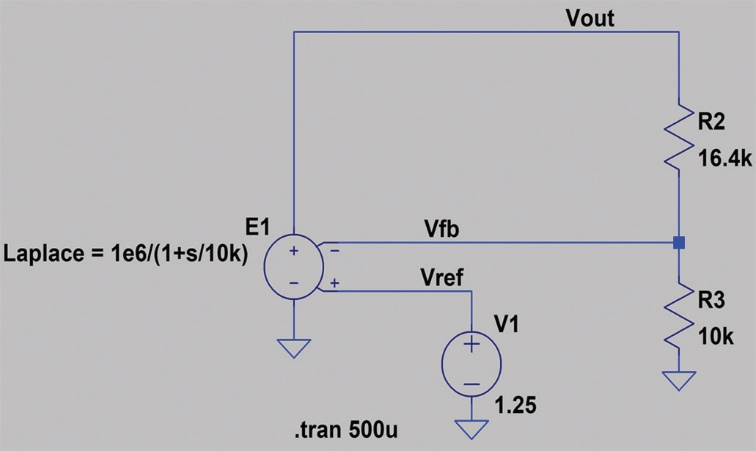
圖6 LTspice DC-DC轉換器仿真原理圖

為了仿真電壓調節的容差分析，反饋電阻R2和R3的容差定義為1%，內部基準電壓的容差定義為1.5%。本節介紹三種容差分析方法：使用蒙特卡羅分布的統計分析、使用高斯分布的統計分析，以及最差情況分析(WCA)。

圖7和圖8顯示使用蒙特卡羅分布仿真的原理圖和電壓調節直方圖。

圖7 使用蒙特卡羅分布進行容差分析的原理圖

圖8 使用蒙特卡羅分布仿真的電壓調節直方圖

圖9和圖10顯示使用高斯分布仿真的原理圖和電壓調節直方圖。

圖9 使用高斯分布進行容差分析的原理圖

圖10 使用高斯分布仿真進行容差分析的直方圖

圖11和圖12顯示使用最差情況分析仿真的原理圖和電壓調節直方圖

圖11 使用最差情況分析仿真進行容差分析的原理圖

圖12 使用WCA進行容差分析的直方圖

表4和圖13比較了容差分析結果。在這個示例中，WCA預測最大偏差，基于高斯分布的仿真預測最小偏差。具體如圖13中的箱形圖所示，箱形表示1-sigma限值，盒須表示最小和最大值。

表4 三種公差分析方法的電壓調節統計匯總

圖13 調節電壓分布的箱形圖比較

總結

本文使用簡化的DC-DC轉換器模型來分析三種變量，使用兩個反饋電阻和內部基準電壓來模擬電壓設定點調節。使用統計分析來展示得出的電壓設定點分布。通過圖表來展示結果。并與最差情況計算結果進行比較。由此得出的數據表明，最差情況下的限值在統計學上是不可能的。

致謝

Simulations were conducted in LTspice.

仿真均在LTspice中完成。

附錄A

附錄A介紹集成電路中經調節基準電壓的統計分布。

在調節前，內部基準電壓采用高斯分布，在調節后，采用蒙特卡羅分布。調節過程通常如下所示：

■   測量調節前的值。此時，通常采用高斯分布。

■   該芯片能否進行微調？如果不能，則放棄該芯片。此步驟基本上會剪除高斯分布的末尾部分。

■   調整數值。這會使基準電壓盡可能接近理想值；數值離理想值越遠，調整的幅度越大。但是，微調分辨率非常精準，所以，接近理想值的基準電壓值不會發生偏移。

■   測量調整后的數值，如果數值可以接受，則鎖定該值。

將得到的分布結果與原來的高斯分布相比，可看到有些數值沒有變化，而其他數值則盡可能接近理想值。生成的直方圖類似于立柱帶有弧形頂部，如圖14所示。

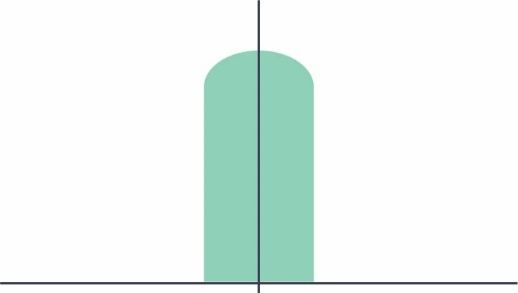
圖14 基準電壓值在調節后的分布圖

雖然這看起來很像是隨機分布，但事實并非如此。如果產品是在封裝后微調，那么其在室溫下的分布圖就如圖14所示。如果產品是在晶圓分類時進行微調，則組裝到塑料封裝時上述分布會再次展開(spread out)。其結果通常是歪斜的高斯分布。

附錄B

附錄B簡要回顧LTspice中提供的高斯分布命令。將回顧sigma = 0.00333和sigma = 0.002時的分布，以及理想分布和仿真的高斯分布之間的一些數值比較。本附錄旨在提供仿真結果的圖表和數值分析。

圖15顯示電阻R1的1001點高斯分布的原理圖。

圖15 5-sigma高斯分布原理圖

值得注意的是對.function語句的修改，將高斯函數的公差定義為tol/5。這導致標準偏差為0.002，或者在1%公差下偏差為1?5。直方圖如圖16所示。

圖16 1001點、5-sigma高斯分布的直方圖，包含50個條形區間

表5顯示1001點仿真的統計分析。值得注意的是，標準偏差為0.001948，而預測偏差為0.002。

表5 5-sigma分布仿真的統計分析

圖17 1001點、3-sigma高斯分布的直方圖，包含50個條形區間

圖17和表6給出了類似的結果，sigma = 0.00333，或者在容差定義為1%時為1?3。

表6 3-Sigma高斯分布仿真的統計分析

附錄C

圖18至圖21以及表7表示1001點蒙特卡羅仿真的原理圖。

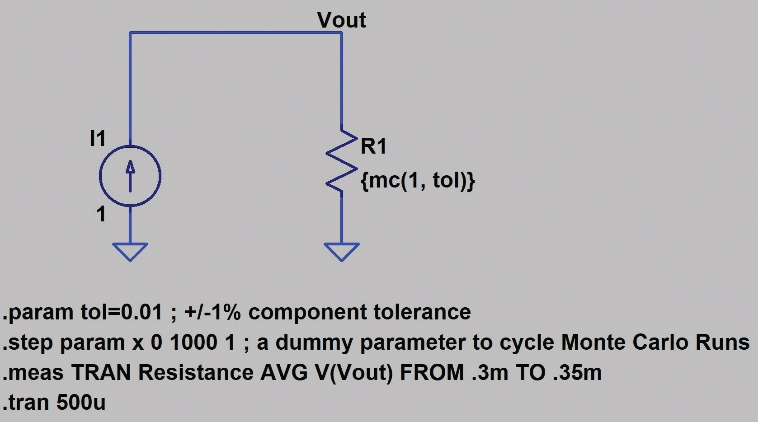
圖18 1001點蒙特卡羅分布仿真的LTspice原理圖

表7 圖18至圖21所示的蒙特卡羅分布仿真的統計分析

圖19 1001點蒙特卡羅分布的1000條形區間直方圖

圖20 1001點蒙特卡羅分布的500條形區間直方圖

圖21 1001點蒙特卡羅分布的50條形區間直方圖

附錄D

附錄D回顧：

■   如何編輯LTspice原理圖來實現容差分析，以及

■   如何使用.measure命令和SPICE錯誤日志。

圖22顯示蒙特卡羅容差分析的原理圖。紅色箭頭表示在.param語句中定義的元件的容差。.param語句屬于SPICE指令。

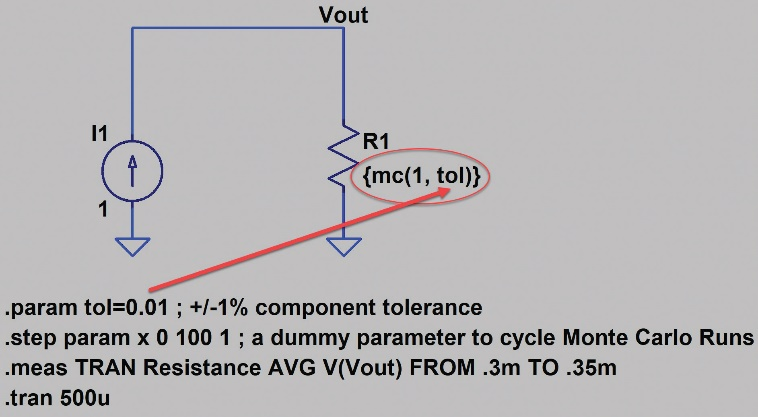
圖22 LTspice中的蒙特卡羅容差分析

可以右鍵單擊元件來編輯R1的電阻值。如圖23所示。

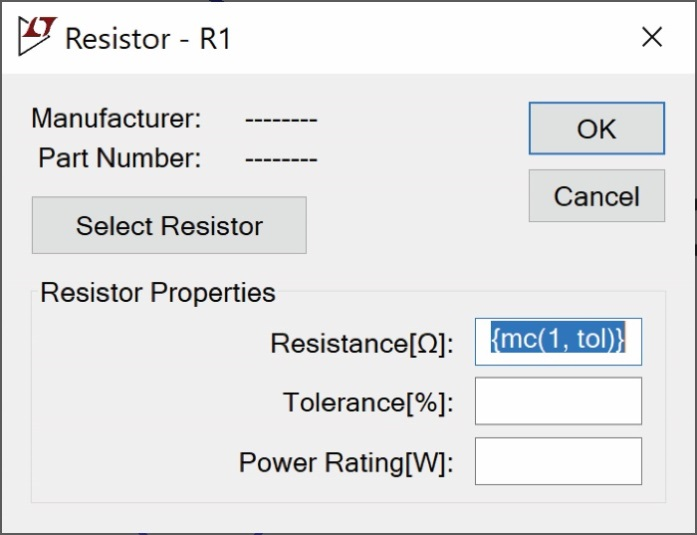
圖23 在LTspice中編輯電阻值

輸入{mc(1, tol)}，將電阻標稱值定義為1，蒙特卡羅分布由參數tol定義。參數tol被定義為SPICE指令。

可以使用控制欄中的SPICE Directive圖標來輸入圖22所示的SPICE指令。如圖24所示。

圖24 在LTspice中輸入SPICE指令

.meas命令可提供一個非常有用GUI，方便您輸入相關參數。如圖25所示。要訪問此GUI，請輸入SPICE指令作為.meas命令。右鍵單擊.meas命令，將會彈出GUI。

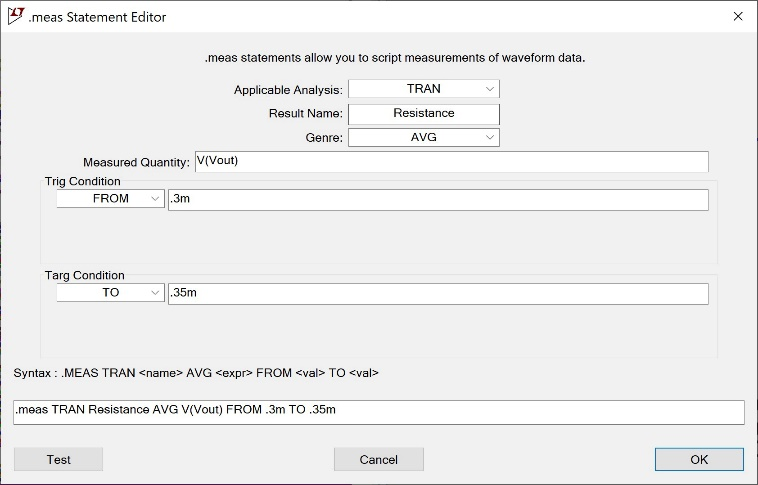
圖25 輸入相關參數的GUI

測量數據記錄在SPICE錯誤日志中。圖26和圖27顯示如何訪問SPICE錯誤日志。

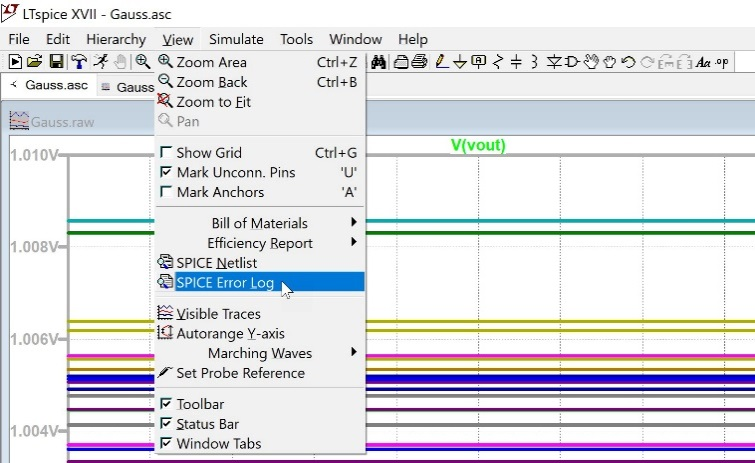
圖26 訪問LTspice錯誤日志

也可以右鍵單擊原理圖，直接從原理圖訪問該錯誤日志，如圖27所示。

圖27 訪問LTspice錯誤日志

打開SPICE錯誤日志會顯示測量值，如圖28所示。可以將這些測量值復制粘貼到Excel中進行數值和圖表分析。

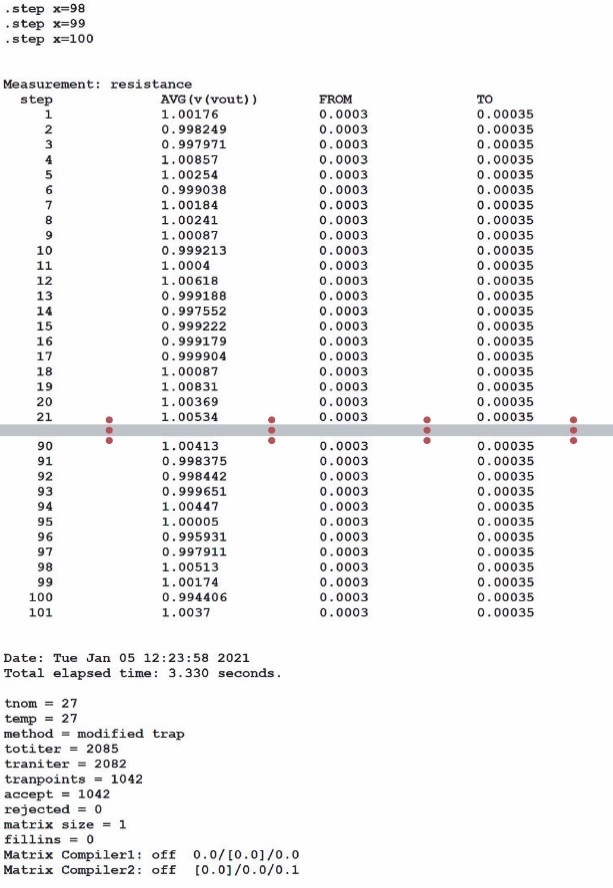
圖28 SPICE錯誤日志圖示，包含來自.meas命令的數據

作者簡介

Steve Knudtsen是ADI公司的一名高級現場應用工程師，工作地點在美國科羅拉多。他畢業于科羅拉多州立大學，擁有電子工程學士學位，自2000年開始，一直在凌力爾特和ADI公司工作。聯系方式：steve.knudtsen@analog.com。