一種基于狀態(tài)觀測(cè)器的PMSM速度觀測(cè)算法
王遠(yuǎn)洋??王?衛(wèi)(湖南工業(yè)大學(xué)?電氣與信息工程學(xué)院,湖南?株洲?412008)
本文引用地址:http://www.104case.com/article/201911/407675.htm摘?要:為了改善低線數(shù)碼盤的測(cè)速精度及碼盤固有的相位滯后問(wèn)題,提出了一種基于狀態(tài)觀測(cè)器的速度觀測(cè)算法。該算法以電機(jī)轉(zhuǎn)矩電流和機(jī)械角度作為輸入量,根據(jù)電機(jī)的數(shù)學(xué)模型和機(jī)械特征方程,構(gòu)建速度觀測(cè)器,來(lái)實(shí)現(xiàn)對(duì)永磁同步電機(jī)速度的精確控制。仿真及實(shí)驗(yàn)結(jié)果表明:該方法與碼盤M法測(cè)速相比,測(cè)得的速度更加精確,并且超調(diào)量小,響應(yīng)快,能起到相位補(bǔ)償?shù)淖饔茫鉀Q了碼盤固有的相位滯后問(wèn)題,同時(shí),在負(fù)載發(fā)生變化時(shí)系統(tǒng)仍然能保持很好的穩(wěn)定性和控制精度。
關(guān)鍵詞:永磁同步電機(jī);碼盤;速度觀測(cè)器;狀態(tài)觀測(cè)器;M法測(cè)速
0 引言
速度是永磁同步電機(jī)控制系統(tǒng)中的一個(gè)重要參數(shù),速度檢測(cè)的精準(zhǔn)性和快速性直接影響著控制系統(tǒng)的性能[1] 。而速度的測(cè)量元件大多是碼盤。利用碼盤作為檢測(cè)元件計(jì)算電機(jī)速度的方法主要有 M 法、T 法、M/T 法[2-3] 以及變M/T 法 [4-6] 。這些方法都是通過(guò)對(duì)碼盤獲取到的脈沖周期和頻率進(jìn)行計(jì)算而得到電機(jī)速度的,當(dāng)電機(jī)處于低速狀態(tài)和碼盤分辨率較低時(shí),這些方法容易出現(xiàn)測(cè)速不精確和與實(shí)際指令跟隨差的問(wèn)題。
為了讓電機(jī)在低速和碼盤分辨率低的情況下也能實(shí)現(xiàn)對(duì)電機(jī)速度的精確控制,需要對(duì)電機(jī)的瞬時(shí)速度進(jìn)行檢測(cè)。電機(jī)的瞬時(shí)速度檢測(cè)方法可分為兩類,一類是通過(guò)檢測(cè)元件檢測(cè)位置的當(dāng)前周期值和上個(gè)周期值然后對(duì)電機(jī)當(dāng)前的瞬時(shí)速度進(jìn)行估計(jì)。文獻(xiàn) [7] 中電機(jī)當(dāng)前周期的瞬時(shí)速度是通過(guò)對(duì)電機(jī)的平均速度來(lái)進(jìn)行估算得到的,以此來(lái)補(bǔ)償速度檢測(cè)所帶來(lái)的延時(shí);文獻(xiàn)通過(guò)碼盤位置值估算電機(jī)的加速度 [8] ,然后對(duì)加速度進(jìn)行積分得到電機(jī)的瞬時(shí)速度。這些方法不受電機(jī)數(shù)學(xué)模型的影響且只利用了碼盤的脈沖信號(hào)。因此,電機(jī)參數(shù)變化對(duì)這類方法的測(cè)量精度無(wú)影響,它只與碼盤的線數(shù)和算法本身有關(guān)。另一類是利用電機(jī)的數(shù)學(xué)模型和機(jī)械特征方程構(gòu)造速度觀測(cè)器 [9] ,對(duì)電機(jī)的瞬時(shí)速度進(jìn)行觀測(cè),這類方法對(duì)系統(tǒng)速度具有預(yù)測(cè)特性,可以提高系統(tǒng)速度環(huán)的響應(yīng)帶寬,大體有全階狀態(tài)觀測(cè)器 [10] 和降階狀態(tài)觀測(cè)器[11] 等。降階狀態(tài)觀測(cè)器算法較簡(jiǎn)單,易實(shí)現(xiàn),但是對(duì)系統(tǒng)噪聲和輸入噪聲敏感,而全階狀態(tài)觀測(cè)器,對(duì)系統(tǒng)噪聲及輸入噪聲有很強(qiáng)的抑制作用,算法復(fù)雜,但隨著處理器性能的提升,讓該算法的實(shí)現(xiàn)成為了可能。本文采用全階狀態(tài)觀測(cè)器作為速度觀測(cè)器的方法。
2 PMSM數(shù)學(xué)模型的建立
2.1 數(shù)學(xué)模型的前提條件
本文以表貼式的PMSM作為研究對(duì)象,由于在工程使用過(guò)程當(dāng)中,PMSM有非線性、約束條件多的特點(diǎn),所以為了便于分析和研究,在對(duì)PMSM基本數(shù)學(xué)模型進(jìn)行建立的時(shí)候需要做一定的假設(shè):
1)不計(jì)鐵芯以及磁路的飽和程度;
2)忽略電機(jī)中電樞鐵芯的渦流損耗;
3)通入空間相隔120電角度的對(duì)稱三相電。
2.2 PMSM數(shù)學(xué)模型
表貼式三相PMSM在 d - q 靜止坐標(biāo)系下等效模型可以表示為 [11] :
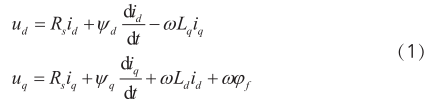
式中: ud uq、分別為定子電壓在 d-q軸的分量; R s為電樞繞組電阻; Ld Lq、分別是 d-q軸電感分量; L s 為電樞電感; id iq、分別為定子電流 d-q軸的分量; φ d 、φ q 為定子磁鏈的 d-q軸分量; ? f 為轉(zhuǎn)子磁鏈; ω 為電角速度。
2.3 PMSM機(jī)械特性方程
PMSM的電機(jī)的轉(zhuǎn)矩和運(yùn)動(dòng)學(xué)方程為:
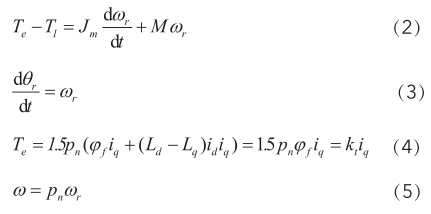
式中: J m 為轉(zhuǎn)動(dòng)慣量; M 為黏滯摩擦系數(shù); T e 為電磁轉(zhuǎn)矩; T l 為負(fù)載轉(zhuǎn)矩; k t 為電機(jī)轉(zhuǎn)矩常數(shù); p n 為電機(jī)極對(duì)數(shù); ω r 為電機(jī)的機(jī)械角速度; θ r 為電機(jī)的機(jī)械角度。
3 狀態(tài)觀測(cè)器的設(shè)計(jì)
3.1 狀態(tài)觀測(cè)器基本原理
狀態(tài)觀測(cè)器又叫狀態(tài)重構(gòu),其基本思想就是用可以測(cè)量的參數(shù)作為輸入量,通過(guò)對(duì)狀態(tài)進(jìn)行重構(gòu),使得估計(jì)得到的狀態(tài)值逼近真實(shí)的狀態(tài)值 [12] 。閉環(huán)狀態(tài)觀測(cè)器的方框圖如圖1所示。
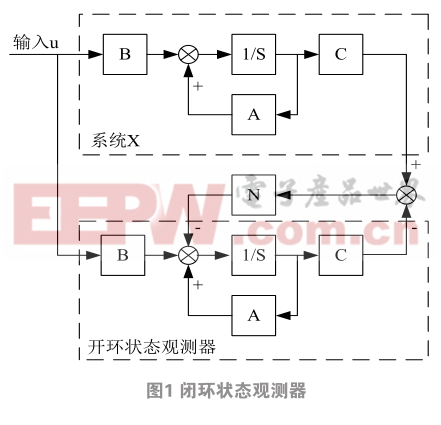
此時(shí),其狀態(tài)方程變?yōu)?/p>
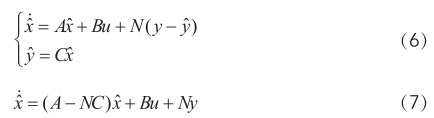
其觀測(cè)誤差方程為:

由式(8)可知誤差特征方程為

由控制理論可知,想要系統(tǒng)穩(wěn)定,就要使式(9)的極點(diǎn)全部分布在s平面左平面,而且系統(tǒng)的極點(diǎn)可以影響到誤差的收斂速度。因此,要使誤差能夠快速的收斂到0,只要通過(guò)引入反饋值并且選擇合適的 N ,就能達(dá)到對(duì)狀態(tài)估計(jì)的作用,而不受狀態(tài)初值的影響。
3.2 狀態(tài)觀測(cè)器的設(shè)計(jì)
忽略黏滯摩擦系數(shù)M,式(3)可重寫為:

式(10)可轉(zhuǎn)化為:

負(fù)載的變化一般是相對(duì)較緩慢的,所以可以認(rèn)為負(fù)載在一個(gè)控制周期內(nèi)是沒(méi)有變化的,即:

另外,由運(yùn)動(dòng)學(xué)定理可知電機(jī)轉(zhuǎn)子在一個(gè)控制周期T a 上的角位移方程如下式:
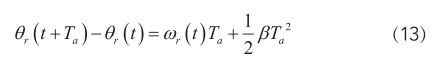
由于控制周期 T a 很小,則(13)可以寫成如下形式:

把式(11)帶入式(14)得:
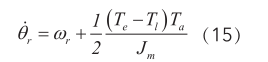
將式(11)(12)和(15)改寫成矩陣形式為:
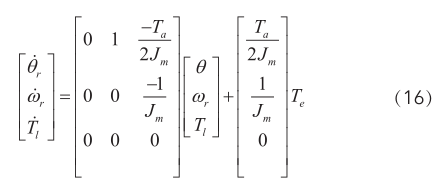
根據(jù)(6)(16)式可構(gòu)造全階狀態(tài)觀測(cè)器模型為:
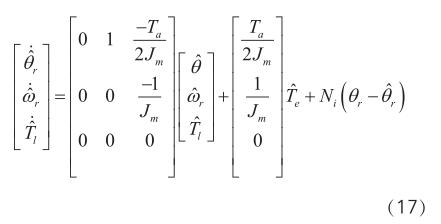
上式中N i 為觀測(cè)器的比例增益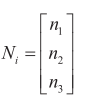
根據(jù)(16)(17)算得其誤差方程為:
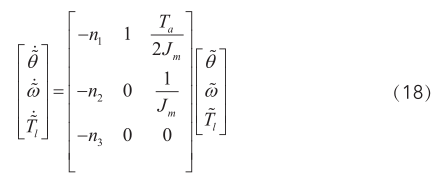
根據(jù)(18)得誤差狀態(tài)方程的特征方程為:
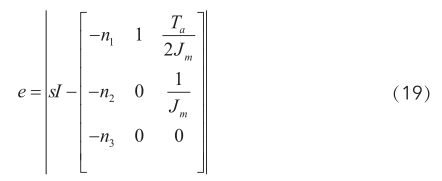
通過(guò)配制 n 1 , n 2 , n 3 的值可以使系統(tǒng)穩(wěn)定并控制其收斂速度。
式(17)離散化到后得到的方程式為:
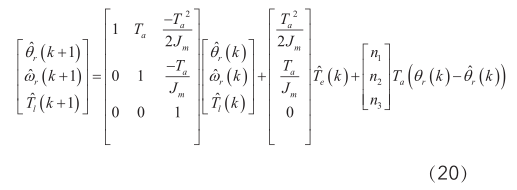
由控制理論可知要使系統(tǒng)收斂只要系統(tǒng)的極點(diǎn)在s平面左半平面,但為了達(dá)到想要的效果,需要選擇合適的極點(diǎn),也就是要讓速度觀測(cè)誤差收斂速度比速度的響應(yīng)要快,即觀測(cè)器的極點(diǎn)比速度閉環(huán)的極點(diǎn)更遠(yuǎn)離原點(diǎn)。但過(guò)大的觀測(cè)器極點(diǎn)值會(huì)引起系統(tǒng)噪聲,導(dǎo)致觀測(cè)誤差,因此對(duì)觀測(cè)器極點(diǎn)的選擇要結(jié)合這兩方面考慮[13] 。
4 系統(tǒng)仿真及實(shí)驗(yàn)結(jié)果
4.1 系統(tǒng)仿真模型
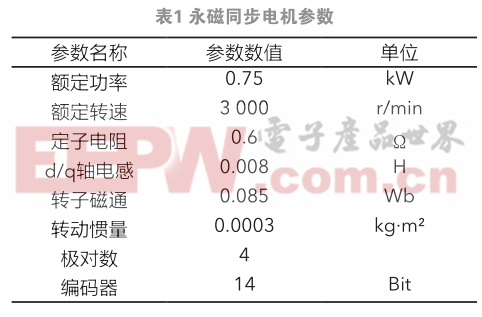
為了便于對(duì)比,Simulink 仿真與實(shí)驗(yàn)平臺(tái)采用的算法和電機(jī)參數(shù)相同。仿真和實(shí)驗(yàn)平臺(tái)中給定速度環(huán)的速度指令也相同。仿真及其實(shí)驗(yàn)電機(jī)參數(shù)見表1。
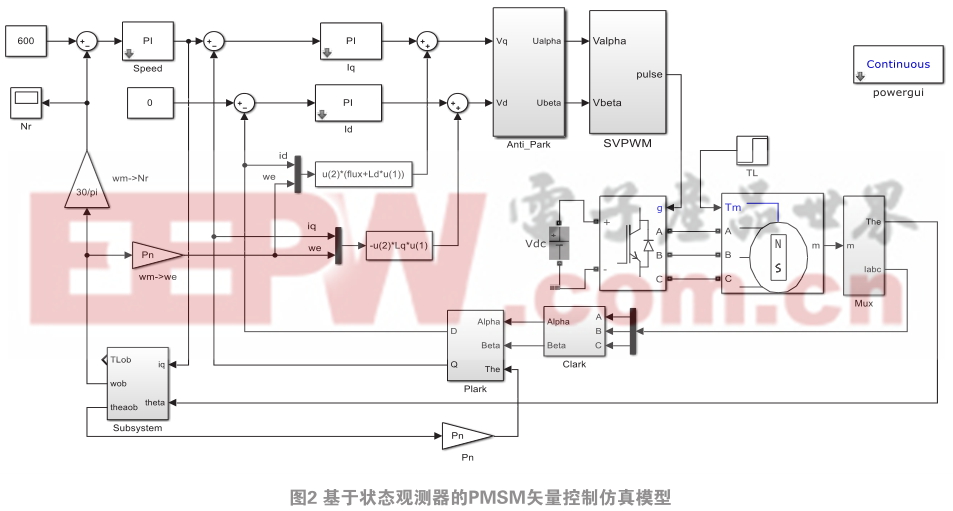
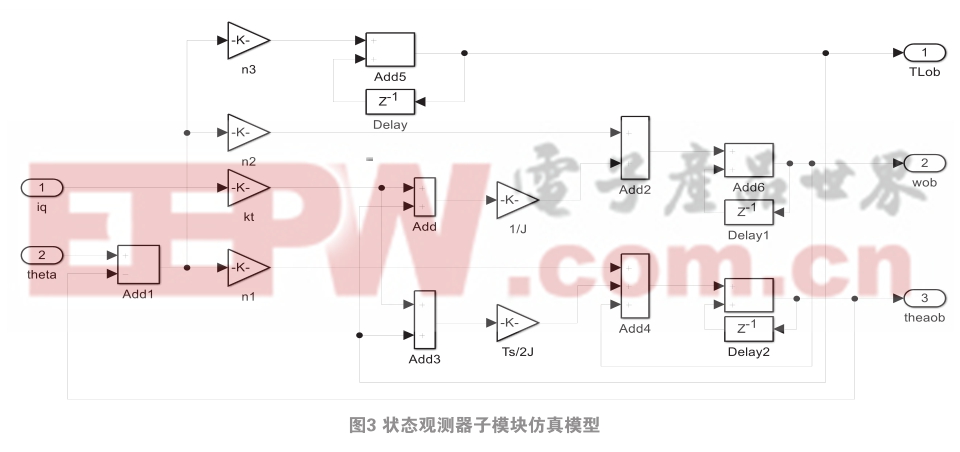
在Matlab/simulink環(huán)境下,根據(jù)前面的理論分析建立了基于狀態(tài)觀測(cè)器的PMSM矢量控制仿真模型,其仿真模型如圖2所示,PMSM矢量控制系統(tǒng)的電流控制方法為 i d = 0 控制,控制周期為125 μs ,狀態(tài)觀測(cè)器子模塊仿真模型如圖3所示。
4.2 仿真結(jié)果分析
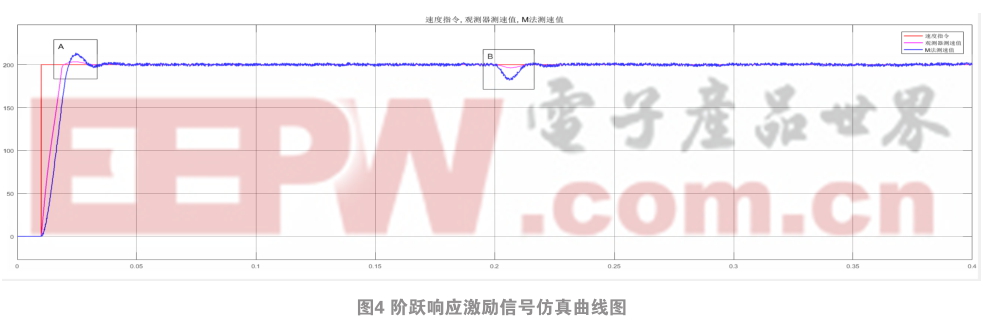
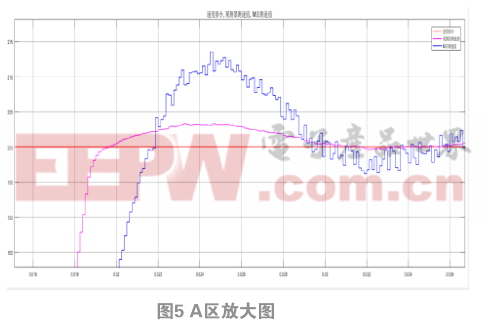
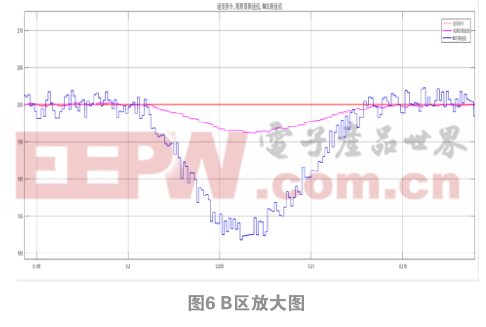
圖4是速度指令為階躍響應(yīng)激勵(lì)信號(hào)時(shí)速度觀測(cè)值與碼盤M法測(cè)速值曲線對(duì)比圖,系統(tǒng)控制周期為125 μs 。從圖中可以看出,系統(tǒng)在0.01 s時(shí)給出速度指令,轉(zhuǎn)速期望值為200 r/min,并且在0.2 s時(shí)加入了2 N.m的擾動(dòng)負(fù)載轉(zhuǎn)矩。從整體波形圖可以看出,碼盤M法測(cè)速值比速度觀測(cè)值轉(zhuǎn)速波動(dòng)大得多。從A區(qū)放大圖中可看出,速度觀測(cè)值大約在0.019 6 s達(dá)到期望值,轉(zhuǎn)速最大值為203 r/min,超調(diào)為1.5%,并且大致在0.031 5 s回歸穩(wěn)定狀態(tài),而碼盤M法測(cè)度值大約0.021 8 s才達(dá)到期望值,轉(zhuǎn)速最大值為214 r/min,超調(diào)達(dá)到了7%,且大致在0.033 2 s才回歸穩(wěn)定狀態(tài),對(duì)比兩組數(shù)據(jù)發(fā)現(xiàn)速度觀測(cè)器得到的速度響應(yīng)快,超調(diào)小。在0.2 s時(shí)加上2N.m的擾動(dòng)負(fù)載轉(zhuǎn)矩,在B區(qū)放大圖中可以看到速度觀測(cè)值很快達(dá)到穩(wěn)定狀態(tài),且沒(méi)有出現(xiàn)較大的轉(zhuǎn)速波動(dòng),而碼盤M法測(cè)速值,達(dá)到穩(wěn)定狀態(tài)時(shí)間長(zhǎng),且轉(zhuǎn)速出現(xiàn)了很大的波動(dòng)。綜上所述,基于狀態(tài)觀測(cè)器的速度觀測(cè)值具有更快的響應(yīng)效率,更高的檢測(cè)精度,更強(qiáng)的平穩(wěn)性。
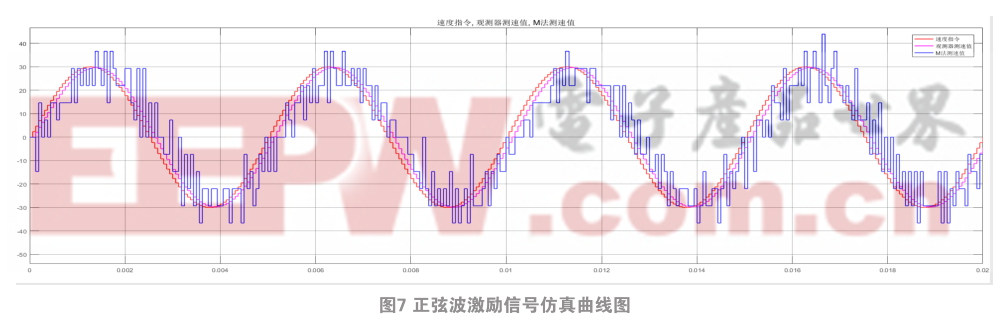
為了更加直觀地看到觀測(cè)器測(cè)速與碼盤M法測(cè)速的區(qū)別,給系統(tǒng)設(shè)定幅值為-30-30 r/min,頻率為200 Hz的正弦波激勵(lì)信號(hào),從圖7可知,速度觀測(cè)值和碼盤M法測(cè)速值都能很好地跟隨速度指令,但是速度觀測(cè)值跟隨的更緊,比碼盤M法測(cè)速值要超前一個(gè)周期,同時(shí),轉(zhuǎn)速波動(dòng)要小很多。因此觀測(cè)器測(cè)速能有效地解決碼盤測(cè)速固有的相位滯后問(wèn)題,且測(cè)速精度更高。
4.3 實(shí)驗(yàn)結(jié)果
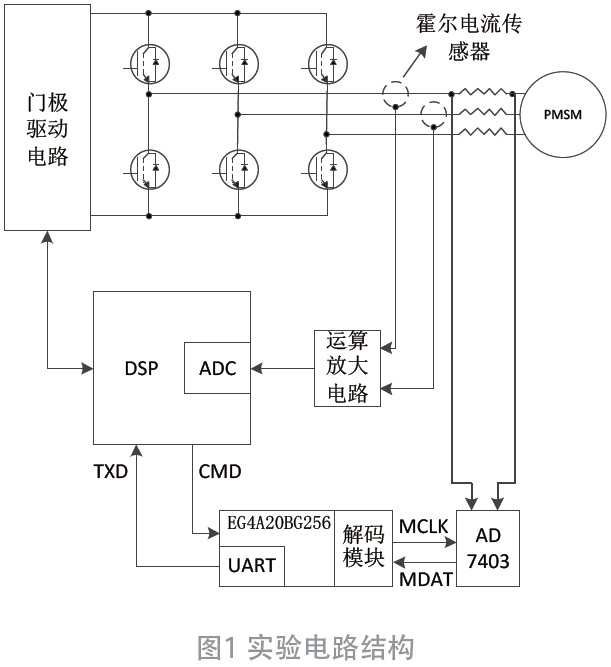
為了檢驗(yàn)狀態(tài)觀測(cè)器在實(shí)際系統(tǒng)中的可行性,進(jìn)行了實(shí)驗(yàn)驗(yàn)證,實(shí)驗(yàn)平臺(tái)如圖 8 所示,采用 ST公司的 32位RAM控制平臺(tái)STM32F407作為主控芯片,系統(tǒng)主要包括上位PC機(jī),表貼式永磁同步電機(jī),RAM控制板,功率板等,系統(tǒng)控制周期為125μs。速度指令及電機(jī)參數(shù)與仿真系統(tǒng)一致,實(shí)驗(yàn)數(shù)據(jù)通過(guò)通訊的方式由 RAM傳送到上位PC機(jī)。

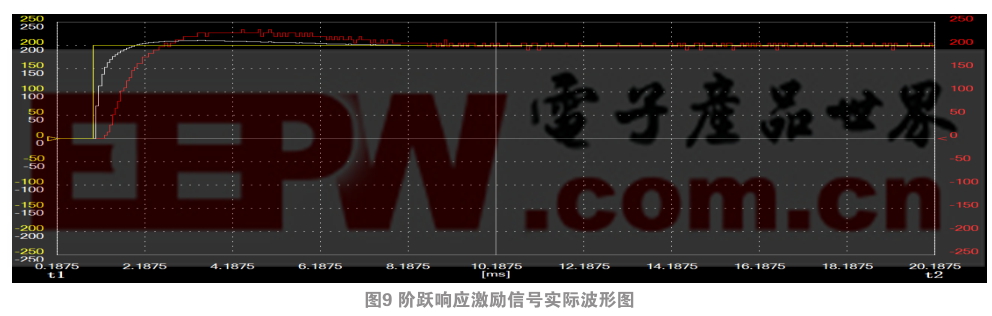
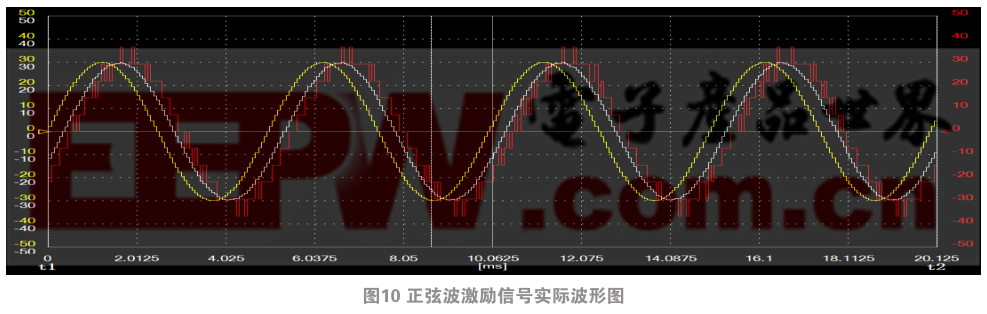
圖9、圖10分別是速度指令為階躍響應(yīng)激勵(lì)信號(hào)和正弦波激勵(lì)信號(hào)時(shí)電機(jī)在實(shí)際系統(tǒng)中速度波形圖,其中,黃色曲線為速度指令,白色曲線為觀測(cè)器測(cè)速值,紅色曲線為M法測(cè)速值,可以看到在實(shí)際系統(tǒng)中速度觀測(cè)器測(cè)得的速度值波動(dòng)小,而且速度曲線較平滑,說(shuō)明其比碼盤M法測(cè)速更具擾動(dòng)修正能力。另外它比碼盤M法測(cè)速的速度值更接近速度指令值,能起到相位補(bǔ)償?shù)淖饔谩?duì)比可知,實(shí)驗(yàn)結(jié)果與仿真結(jié)果基本一致,這充分證明了基于狀態(tài)觀測(cè)器的速度觀測(cè)算法在實(shí)際系統(tǒng)中的有效性。
5 結(jié)論
本文對(duì)永磁同步電機(jī)測(cè)速方法進(jìn)行了研究和分析,提出了利用狀態(tài)觀測(cè)器作為測(cè)速方法,并對(duì)狀態(tài)觀測(cè)器進(jìn)行設(shè)計(jì),通過(guò)對(duì)狀態(tài)觀測(cè)器測(cè)速方法和碼盤M法測(cè)速方法進(jìn)行比較。仿真及實(shí)驗(yàn)結(jié)果表明,使用狀態(tài)觀測(cè)器的測(cè)速方法比碼盤M測(cè)速法的方法有更好的穩(wěn)定性,更高的精準(zhǔn)性和更強(qiáng)的適應(yīng)性,并且狀態(tài)觀測(cè)器有相位超前的功能,能很好地解決碼盤測(cè)速固有的相位滯后問(wèn)題,起到相位補(bǔ)償?shù)淖饔茫瑫r(shí)狀態(tài)觀測(cè)器能在碼盤線數(shù)較低的前提下實(shí)現(xiàn)對(duì)速度的精確控制,能大大地降低產(chǎn)品的成本,具有很大的實(shí)際意義。
參考文獻(xiàn)
[1] 楊興華,姜建國(guó).永磁同步電機(jī)精確瞬時(shí)速度檢測(cè)[J].電工技術(shù)學(xué)報(bào),2011,26(04):71-76.
[2] Tsuji T, Mizuochi M, Nishi H, et al.A velocity measurement method foracceleration control[C]. 31st IndustrialElectronics Society Annual Conferenceof IEEE, 2005: 1943-1948.
[3] 李勇,潘松峰.基于DSP的M/T法測(cè)速研究[J].工業(yè)控制計(jì)算機(jī),2018,31(05):145-146.
[4] 徐張旗,陶家園,王克逸,簡(jiǎn)慧杰.基于卡爾曼濾波的新型變“M/T”編碼器測(cè)速方法[J].新技術(shù)新工藝,2018(09):28-31.
[5] 王海勇,鮑遠(yuǎn)慧.一種變M/T測(cè)速方法的研究與實(shí)驗(yàn)[J].測(cè)控技術(shù),2014,33(05):146-149.
[6] 趙帥,肖金壯,郭一.基于改進(jìn)型卡爾曼濾波的電機(jī)速度數(shù)據(jù)處理方法[J].微特電機(jī),2018,46(09):80-82.
[7] Wang Gaolin, Xu Dianguo, Yu Yong,et al. Low speed control of permanentmagnet synchronous motor based oninstantaneous speed estimation[C].The Sixth World Congress on IntelligentControl and Automation, 2006, 2: 8033-8036.
[8] Lee Se Han, Song Jae Bok. Accelerationestimator for low-velocity and low-acceleration regions based on encoderposition data[J]. IEEE/ASME Transactionson Mechatronics, 2001, 6(1): 58-64.
[9] 張永瀾. 狀態(tài)觀測(cè)器在伺服控制系統(tǒng)中的應(yīng)用研究[D].哈爾濱:哈爾濱工業(yè)大學(xué),2007.
[10] 羅桂山.基于全階狀態(tài)觀測(cè)的無(wú)速度傳感器矢量控制仿真[J].機(jī)電設(shè)備,2017,34(03):26-30.
[11] 劉玉燕,劉吉臻,周世梁.基于降階狀態(tài)觀測(cè)器的壓水堆功率自抗擾控制[J].中國(guó)電機(jī)工程學(xué)報(bào),2017,37(22):6666-6674+6779.
[12] 沈陽(yáng),舒志兵,朱爾立,吳晨軍,高春寶.Luenbeger速度觀測(cè)器在交流伺服系統(tǒng)中的設(shè)計(jì)與研究[J].微電機(jī),2016,49(03):87-89.
[13] 宋成. 交流永磁同步電機(jī)的速度觀測(cè)器研究及實(shí)現(xiàn)[D].哈爾濱:哈爾濱工業(yè)大學(xué),2011.
本文來(lái)源于科技期刊《電子產(chǎn)品世界》2019年第12期第68頁(yè),歡迎您寫論文時(shí)引用,并注明出處。








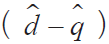

評(píng)論