擴展卡爾曼濾波器在同步電機無速度矢量控制系統中的應用

作者　閔翔宇 劉斌 湖南工業大學 電氣與信息工程學院(湖南 株洲 412000)

　　閔翔宇(1991-)，男，碩士生，研究方向：永磁同步電機無傳感器控制;劉斌，男，博士，教授，研究方向：魯棒控制及復雜系統。

摘要：針對機械式速度傳感器存在的系統復雜、適應性低以及成本高的問題，研究了一種基于擴展卡爾曼濾波器的無速度傳感器同步電機矢量控制系統，其在不改變電機本體機構的基礎上，使得同步電機矢量控制系統具有較強的適應性以及較低的成本，且可以精確地預測出電機的轉速。

0 引言

　　矢量技術是目前應用比較廣泛的電機調速技術^[1]，其采用雙閉環控制，且外環需要轉速作為反饋，同時坐標變換需要轉子磁極的位置信號，以實現轉子磁場與電樞電流在空間上的正交，使得在一定條件下產生的電磁轉矩最大^[2]。因此，得到準確的轉子磁極的速度和位置信號是實現該控制系統的關鍵。傳統方法中都是用機械傳感器來直接檢測得到的，但安裝機械速度傳感器以后會帶來很多弊端，例如系統復雜、適應性低、成本高。針對這個問題本文將擴展卡爾曼濾波算法應用到永磁同步電機矢量控制系統中，改進后的系統具有不改變電動機結構、安裝維護簡單、受環境變化影響小、成本低等眾多優點。

　　永磁同步電機的數學模型

　　定子電壓方程為：

1 SVPWM基本原理

　　在一個周期不同作用時間內，通過控制開關器件的開關狀態得到期望的電壓空間矢量，進而得到近似的圓形磁鏈，此為SVPWM的基本原理。

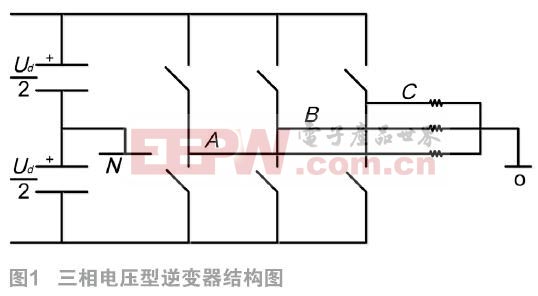
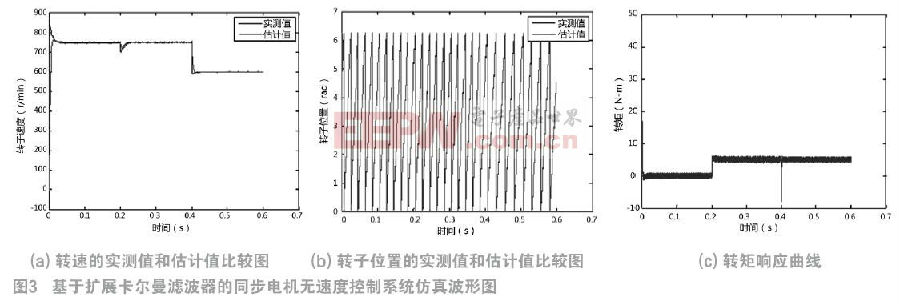
　　由圖1可知，設A、B、C三相橋臂的開關狀態分別為S_A、S_B、S_C，S_A=1，S_B=1，S_C=1時，分別代表A、B、C相橋臂的上橋臂開通、下橋臂關斷。逆變器的開關器件的開關組合有八種，每一種組合得到的三相電壓都會合成一種基本空間電壓矢量，所以就有八種基本空間電壓矢量。按功率平衡原則可以得到公式(4)：

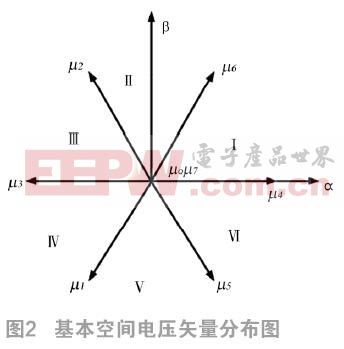
　　以此類推，可以得到其它七個基本空間電壓矢量，在這其中，八個基本空間電壓矢量中，有兩個零矢量μ₀、μ₁和六個有效工作矢量μ₁~μ₆，此八個空間電壓矢量將平面分為對稱的六個扇區，如圖2所示。所需要的電壓矢量，可以利用八個基本電壓矢量進行合成。

2 卡爾曼濾波器

　　卡爾曼濾波器采用遞歸算法，利用系統當前的已知信息(包括系統的觀測序列和前一時刻的狀態)去估計系統的狀態變量^[3-5]。因為它其會利用反饋對估計的狀態變量進行修正，使估計的誤差方差減小，所以卡爾曼濾波器是一種最優估計算法。卡爾曼濾波器是一種線性估計，即要求估計的狀態和觀測序列與狀態是線性關系。卡爾曼濾波器方程為：

3 擴展卡爾曼濾波器同步電機矢量控制中的應用

　　卡爾曼濾波器只能對離散線性模型進行狀態估計，對于離散非線性系統，可以將模型在狀態估計值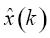附近進行線性化，再采用卡爾曼濾波器;對于連續非線性系統，可以先線性化、離散化，再采用卡爾曼濾波器，這就是擴展卡爾曼濾波器^[6-7]。構建電機的擴展卡爾曼濾波器方程，首先要建立電機的非線性數學模型。

　　將公式(7)和公式(9)可以得到電機的擴展卡爾曼濾波器方程為：

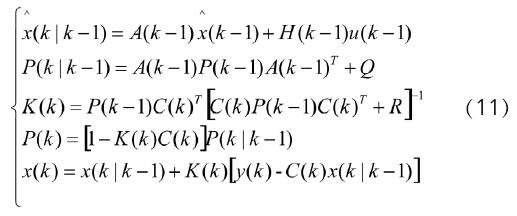
4 仿真分析

　　為了驗證系統性能，本文針對同步電機矢量控制系統進行了仿真實驗分析。本仿真釆用的電機參數如下：

　　額定功率P_N=2 kW，額定轉速n_r=2000 r/min ，額定電壓U_N=300 V，定子電阻R_s=0.9585 Ω，定子電感L_s=0.00525 mH，轉子磁鏈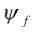=0.1827 Wb，轉動慣量J=0.000633 kg·m2，粘滯系數B=0.0003035 N·m·s，轉子的極對數P_n=4。

　　本文仿真算法為ode23tb，系統初始給定轉速為750 r/min，電機空載啟動0.2 s突加4 N·m負載，0.4 s時轉速給定變為600 r/min，仿真時間0.6 s，EKF采樣時間選為1e-4s，P₀、x₀、Q、R的選擇為：

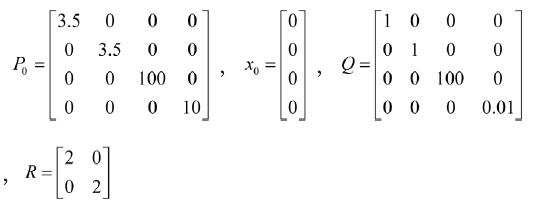
　　如圖3所示，圖中分別給出了轉子速速、位置的實測值和估計值比較以及電磁轉矩波形。

　　由圖3(a)可知，擴展卡爾曼濾波器的輸出轉速波形與電機實際轉速波形非常接近，估計轉速與實際轉速基本一致，能夠較好的反映轉速的動靜態性能。在電機負載轉矩變化的情況下，估計轉速也能夠很快趨于穩定，與實際轉速一致。

　　由圖3(b)可知，卡爾曼濾波器估算的轉子位置角精度很高且當負載發生突變后，濾波器估算電機位置和轉速信號與實際信號很接近，具有很高的跟蹤精度。力矩的變化對轉子位置角的影響極小，說明系統抗負載擾動能力較強且速度閉環起到了很好的調節作用，驗證了擴展卡爾曼濾波器對于同步電機無速度控制的有效性。

　　由圖3(c)可知，電機以最大轉矩啟動，并迅速達到給定值，轉矩變化時也能夠實現快速跟蹤。

5 結論

　　本文將擴展卡爾曼濾波器算法應用到同步電機的無速度傳感器矢量控制系統中，得到了較好的應用效果，不僅可以準確的估算出電機的轉速，而且能夠對轉矩實現快速跟蹤，具有良好的應用價值。

　　參考文獻：

　　[1]王鑫,李偉力,程樹康.永磁同步電動機發展展望[J].微電機,2007,40(5):69-72.

　　[2]許峻峰.提高永磁同步電動機調速系統性能方法研究[D].成都:西南交通大學,2005.

　　[3]谷善茂,何鳳友,譚國俊,等.擴展卡爾曼濾波的PMSM無傳感器低速性能研究[J].電氣傳動,2009,39 (18):12-18.

　　[4]丁信忠,張承瑞,李虎修,等.基于自適應擴展卡爾曼濾波器的永磁同步電機超低速控制[J].電機與控制應用,2012,39(9):24-29.

　　[5]劉祖全.基于卡爾曼濾波算法的永磁同步電機無速度傳感器控制研究[D].濟南:山東大學,2009.

　　[6]陳潔.基于EKF無位置傳感器永磁同步電機控制系統的研究[D].南充:西南石油大學,2012.

　　[7]馬志勛.電勵磁同步電機無傳感器矢量控制系統研究[M].徐州:中國礦業大學,2009.

　　本文來源于《電子產品世界》2018年第8期第61頁，歡迎您寫論文時引用，并注明出處。