快速傅里葉變換FFT的C程序代碼實(shí)現(xiàn)

　　一、徹底理解傅里葉變換

　　快速傅里葉變換(Fast Fourier Transform)是離散傅里葉變換的一種快速算法，簡稱FFT，通過FFT可以將一個信號從時域變換到頻域。
　　模擬信號經(jīng)過A/D轉(zhuǎn)換變?yōu)閿?shù)字信號的過程稱為采樣。為保證采樣后信號的頻譜形狀不失真，采樣頻率必須大于信號中最高頻率成分的2倍，這稱之為采樣定理。
　　假設(shè)采樣頻率為fs，采樣點(diǎn)數(shù)為N，那么FFT結(jié)果就是一個N點(diǎn)的復(fù)數(shù)，每一個點(diǎn)就對應(yīng)著一個頻率點(diǎn)，某一點(diǎn)n(n從1開始)表示的頻率為：fn=(n-1)*fs/N。
　　舉例說明：用1kHz的采樣頻率采樣128點(diǎn)，則FFT結(jié)果的128個數(shù)據(jù)即對應(yīng)的頻率點(diǎn)分別是0，1k/128，2k/128，3k/128，…，127k/128 Hz。
　　這個頻率點(diǎn)的幅值為：該點(diǎn)復(fù)數(shù)的模值除以N/2(n=1時是直流分量，其幅值是該點(diǎn)的模值除以N)。

　　二、傅里葉變換的C語言編程

　　1、對于快速傅里葉變換FFT，第一個要解決的問題就是碼位倒序。

　　假設(shè)一個N點(diǎn)的輸入序列，那么它的序號二進(jìn)制數(shù)位數(shù)就是t=log2N.
　　碼位倒序要解決兩個問題：①將t位二進(jìn)制數(shù)倒序;②將倒序后的兩個存儲單元進(jìn)行交換。
　　如果輸入序列的自然順序號i用二進(jìn)制數(shù)表示，例如若最大序號為15，即用4位就可表示n3n2n1n0，則其倒序后j對應(yīng)的二進(jìn)制數(shù)就是n0n1n2n3，那么怎樣才能實(shí)現(xiàn)倒序呢?利用C語言的移位功能!
　　程序如下，我不多說，看不懂者智商一定在180以下!

　　復(fù)數(shù)類型定義及其運(yùn)算
　　#define N 64 //64點(diǎn)
　　#define log2N 6 //log2N=6
　　/*復(fù)數(shù)類型*/
　　typedef struct
　　{
　　float real;
　　float img;
　　}complex;
　　complex xdata x[N]; //輸入序列
　　/*復(fù)數(shù)加法*/
　　complex add(complex a,complex b)
　　{
　　complex c;
　　c.real=a.real+b.real;
　　c.img=a.img+b.img;
　　return c;
　　}
　　/*復(fù)數(shù)減法*/
　　complex sub(complex a,complex b)
　　{
　　complex c;
　　c.real=a.real-b.real;
　　c.img=a.img-b.img;
　　return c;
　　}
　　/*復(fù)數(shù)乘法*/
　　complex mul(complex a,complex b)
　　{
　　complex c;
　　c.real=a.real*b.real - a.img*b.img;
　　c.img=a.real*b.img + a.img*b.real;
　　return c;
　　}
　　/***碼位倒序函數(shù)***/
　　void Reverse(void)
　　{
　　unsigned int i,j,k;
　　unsigned int t;
　　complex temp;//臨時交換變量
　　for(i=0;iN;i++)//從第0個序號到第N-1個序號
　　{
　　k=i;//當(dāng)前第i個序號
　　j=0;//存儲倒序后的序號，先初始化為0
　　for(t=0;tlog2N;t++)//共移位t次，其中l(wèi)og2N是事先宏定義算好的
　　{
　　j=1;
　　j|=(k1);//j左移一位然后加上k的最低位
　　k>>=1;//k右移一位，次低位變?yōu)樽畹臀?br />　　}
　　if(j>i)//如果倒序后大于原序數(shù)，就將兩個存儲單元進(jìn)行交換(判斷j>i是為了防止重復(fù)交換)
　　{
　　temp=x;
　　x=x[j];
　　x[j]=temp;
　　}
　　}
　　}

　　2、第二個要解決的問題就是蝶形運(yùn)算

　　①第1級(第1列)每個蝶形的兩節(jié)點(diǎn)“距離”為1，第2級每個蝶形的兩節(jié)點(diǎn)“距離”為2，第3級每個蝶形的兩節(jié)點(diǎn)“距離”為4，第4級每個蝶形的兩節(jié)點(diǎn)“距離”為8。由此推得，
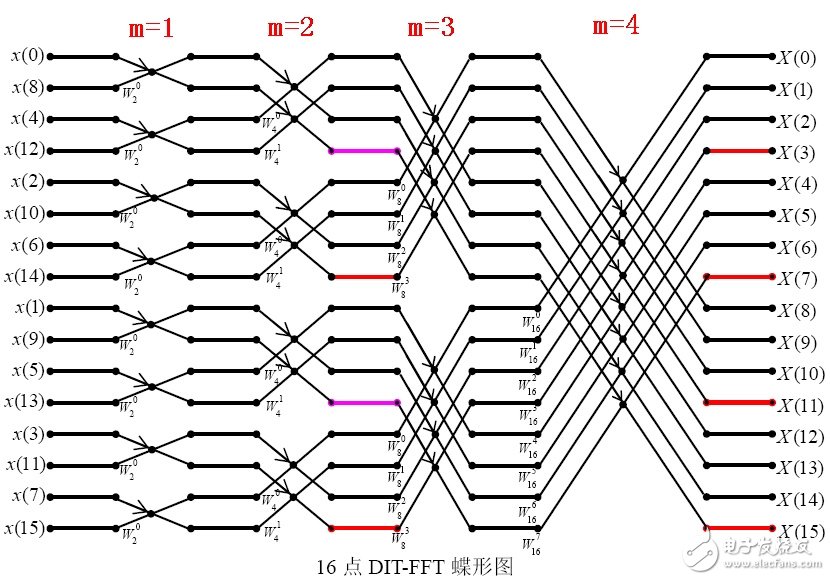
　　第m級蝶形運(yùn)算，每個蝶形的兩節(jié)點(diǎn)“距離”L=2m-1。
　　②對于16點(diǎn)的FFT，第1級有16組蝶形，每組有1個蝶形;第2級有4組蝶形，每組有2個蝶形;第3級有2組蝶形，每組有4個蝶形;第4級有1組蝶形，每組有8個蝶形。由此可推出，
　　對于N點(diǎn)的FFT，第m級有N/2L組蝶形，每組有L=2m-1個蝶形。
　　③旋轉(zhuǎn)因子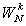的確定
　　以16點(diǎn)FFT為例，第m級第k個旋轉(zhuǎn)因子為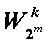，其中k=0～2m-1-1，即第m級共有2m-1個旋轉(zhuǎn)因子，根據(jù)旋轉(zhuǎn)因子的可約性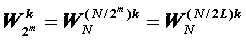，，所以第m級第k個旋轉(zhuǎn)因子為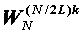，其中k=0～2m-1-1。

　　為提高FFT的運(yùn)算速度，我們可以事先建立一個旋轉(zhuǎn)因子數(shù)組，然后通過查表法來實(shí)現(xiàn)。

　　complex code WN[N]=//旋轉(zhuǎn)因子數(shù)組
　　{ //為節(jié)省CPU計算時間，旋轉(zhuǎn)因子采用查表處理
　　//★根據(jù)實(shí)際FFT的點(diǎn)數(shù)N，該表數(shù)據(jù)需自行修改
　　//以下結(jié)果通過Excel自動生成
　　// WN[k].real=cos(2*PI/N*k);
　　// WN[k].img=-sin(2*PI/N*k);
　　{1.00000,0.00000},{0.99518,-0.09802},{0.98079,-0.19509},{0.95694,-0.29028},
　　{0.92388,-0.38268},{0.88192,-0.47140},{0.83147,-0.55557},{0.77301,-0.63439},
　　{0.70711,-0.70711},{0.63439,-0.77301},{0.55557,-0.83147},{0.47140,-0.88192},
　　{0.38268,-0.92388},{0.29028,-0.95694},{0.19509,-0.98079},{0.09802,-0.99518},
　　{0.00000,-1.00000},{-0.09802,-0.99518},{-0.19509,-0.98079},{-0.29028,-0.95694},
　　{-0.38268,-0.92388},{-0.47140,-0.88192},{-0.55557,-0.83147},{-0.63439,-0.77301},
　　{-0.70711,-0.70711},{-0.77301,-0.63439},{-0.83147,-0.55557},{-0.88192,-0.47140},
　　{-0.92388,-0.38268},{-0.95694,-0.29028},{-0.98079,-0.19509},{-0.99518,-0.09802},
　　{-1.00000,0.00000},{-0.99518,0.09802},{-0.98079,0.19509},{-0.95694,0.29028},
　　{-0.92388,0.38268},{-0.88192,0.47140},{-0.83147,0.55557},{-0.77301,0.63439},
　　{-0.70711,0.70711},{-0.63439,0.77301},{-0.55557,0.83147},{-0.47140,0.88192},
　　{-0.38268,0.92388},{-0.29028,0.95694},{-0.19509,0.98079},{-0.09802,0.99518},
　　{0.00000,1.00000},{0.09802,0.99518},{0.19509,0.98079},{0.29028,0.95694},
　　{0.38268,0.92388},{0.47140,0.88192},{0.55557,0.83147},{0.63439,0.77301},
　　{0.70711,0.70711},{0.77301,0.63439},{0.83147,0.55557},{0.88192,0.47140},
　　{0.92388,0.38268},{0.95694,0.29028},{0.98079,0.19509},{0.99518,0.09802}
　　};

　　3、算法實(shí)現(xiàn)

　　我們已經(jīng)知道，N點(diǎn)FFT從左到右共有l(wèi)og2N級蝶形，每級有N/2L組，每組有L個。所以FFT的C語言編程只需用3層循環(huán)即可實(shí)現(xiàn)：最外層循環(huán)完成每一級的蝶形運(yùn)算(整個FFT共log2N級)，中間層循環(huán)完成每一組的蝶形運(yùn)算(每一級有N/2L組)，最內(nèi)層循環(huán)完成單獨(dú)1個蝶形運(yùn)算(每一組有L個)。
　　/***【快速傅里葉變換】***/
　　void FFT(void)
　　{
　　unsigned int i,j,k,l;
　　complex top,bottom,xW;
　　Reverse(); //碼位倒序
　　for(i=0;ilog2N;i++) /*共log2N級*/
　　{ //一級蝶形運(yùn)算
　　l=1i;//l等于2的i次方
　　for(j=0;jN;j+=2*l) /*每L個蝶形是一組，每級有N/2L組*/
　　{ //一組蝶形運(yùn)算
　　for(k=0;kl;k++) /*每組有L個*/
　　{ //一個蝶形運(yùn)算
　　xW=mul(x[j+k+l],WN[N/(2*l)*k]); //碟間距為l
　　top=add(x[j+k],xW); //每組的第k個蝶形
　　bottom=sub(x[j+k],xW);
　　x[j+k]=top;
　　x[j+k+l]=bottom;
　　}
　　}
　　}
　　}

　　三、FFT計算結(jié)果驗(yàn)證

　　隨便輸入一個64點(diǎn)序列，例如
　　x[N]={{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0},{8,0},{4,0},{1,0},{3,0},{2,0},{5,0}};
　　在Keil中Debug查看數(shù)組變量x的FFT計算結(jié)果并與MATLAB計算結(jié)果進(jìn)行比對，可以發(fā)現(xiàn)非常準(zhǔn)確，說明程序編寫正確！