精通信號處理設計小Tips（8）：檢測淹沒在噪聲中的信號

　　本文作者maxfiner，畢業于西安電子科技大學，擁有信號與信息處理專業碩士學位。maxfiner曾供職于華為通信技術公司無線通信部門，擁有多年的工程項目研發經驗，同時兼備算法理論研究，仿真驗證，以及對應的硬件設計實現能力；具備通信物理層開發設計各個方面的實戰經驗...

　　相關函數的應用很廣，比如噪聲中信號的檢測，信號中隱含周期性的檢測，信號時延長度的測量等等。這一節專門討論利用自相關函數檢測淹沒在噪聲下的周期性信號。

　　一個信號，由于噪聲的影響，從波形上看，已經面目全非，雜亂不堪。如下圖所示：

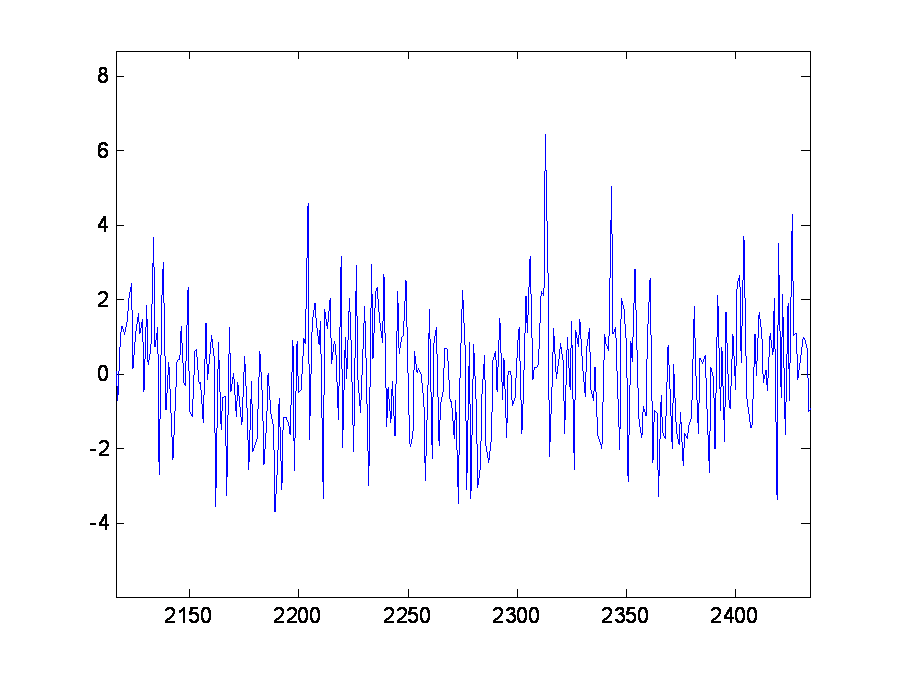
　　基于信號的自相關累積可以檢測是否有周期信號的存在，這是基于幾個前提：

　　第一，通常把噪聲都看作加性的白噪聲對待，因為這種噪聲從理論上便于分析和處理。而白噪聲的自相關函數有著非常獨特的個性，就是自相關函數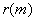只在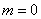時有一定的數值，在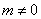則為零值。這是白噪聲本身的完全隨機性決定的。也正是基于這個性質，我們才有可能從強噪聲背景中提取出我們感興趣的信號。

　　第二，周期信號的自相關函數，仍是周期函數，并且周期和原函數周期相同。這從自相關函數的定義可以很容易推導出來。

　　第三，白噪聲和周期信號完全不相關，白噪聲的完全隨機性導致它和任何函數都不相關戀。它們之間的互相關函數可認為是零。這是很多理論推導的一個前提。

　　基于自相關函數的定義，我們可以從公式上做一下簡單的推導，看看添加了噪聲后的信號的自相關函數到底是什么樣子。假定我們的信號為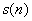，白噪聲信號為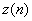，則添加了白噪聲的信號為。

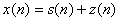　　那么，基于上面的三個前提，我們可以把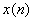的自相關函數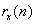表示成如下的形式。公式推導看上去很麻煩，其實一步一步都有嚴格的規律和理由，認真觀察和分析，可以增進對自相關函數和互相關函數的理解，也可以加強公式推導的基礎能力。

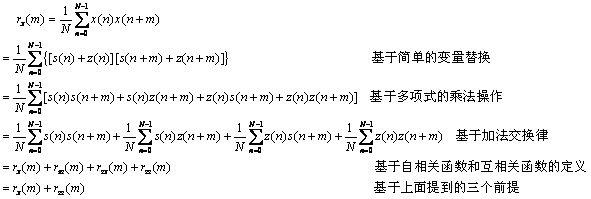
也就是說，

　　理論公式非常嚴密但不直觀。還是找個實際例子驗證下吧。構造一個正弦波周期信號和白噪聲信號，看看它們疊加后的信號的自相關函數到底是個什么樣子。

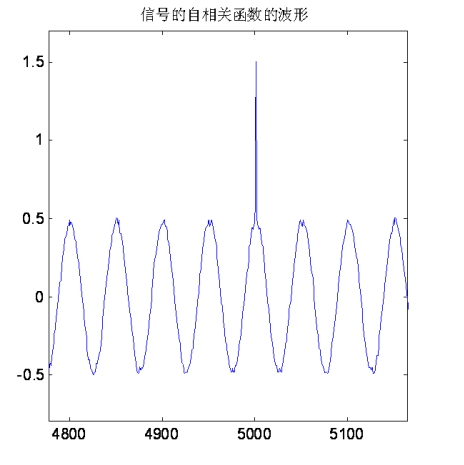
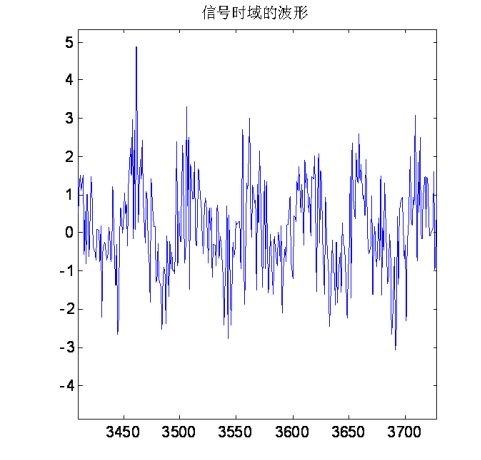
　　自相關函數在0位置是一個相對較大的數值，這是白噪聲自身相關累積導致的。在非零位置，則完全由周期信號來決定了。

　　相應的matlab仿真驗證代碼如下，

　　fs = 5e3;

　　n = 0:1/fs:1;

　　len = length（n）;

　　freq = 100;

　　s = sin（2*pi*freq*n）;

　　n = randn（1，len）;

　　x = s + n;

　　rr = xcorr（x，‘unbiased’）;

　　figure，subplot（121），plot（x）;TItle（‘ÐźÅʱÓòµÄ²¨ÐÎ’）;

　　subplot（122），plot（rr）;TItle（‘ÐźŵÄ&TImes;ÔÏà¹Øº¯ÊýµÄ²¨ÐÎ’）;

　　值得說明的是，相關函數采用matlab工具箱提供的函數xcorr，它有兩種計算方式，一種叫“biased”，即有偏的。一種叫“unbiased”，即無偏的。這是由于實際計算相關函數時，實際數據的長度總是有限的，那么隨著相關函數中m的增大，相關累積求和的樣點數是逐漸減小的，當采用上面提到的自相關函數計算公式時，統一都除以N，導致相關函數隨著m的增大會線性減，這就是有偏的計算方式，意思是計算值的統計上的均值和實際值之間并不一致，存在一定的偏差。這種計算方式導致當m的絕對值接近實際采集信號長度N時，誤差會變得越來越大。若是把m的增大導致累積樣點減少這個因素考慮進去，不再統一除以N，而是除以N-m，則相關函數不再會產生線性減小的問題，這就對應代碼中的無偏的計算方式。

下期開講——精通信號處理設計小TIps（9）：估算信號在模擬通道的延時，敬請關注！

聲明：電子發燒友網版權所有，謝絕轉載！