Nature重磅：Hinton、LeCun、Bengio三巨頭權威科普深度學習

　　借助深度學習，多處理層組成的計算模型可通過多層抽象來學習數據表征( representations)。這些方法顯著推動了語音識別、視覺識別、目標檢測以及許多其他領域(比如，藥物發現以及基因組學)的技術發展。利用反向傳播算法(backpropagation algorithm)來顯示機器將會如何根據前一層的表征改變用以計算每層表征的內部參數，深度學習發現了大數據集的復雜結構。深層卷積網絡(deep convolutional nets)為圖像、視頻和音頻等數據處理上帶來突破性進展，而遞歸網絡(recurrent nets )也給序列數據(諸如文本、語言)的處理帶來曙光。

　　機器學習為現代生活諸多方面帶來巨大動力：從網頁搜索到社交網絡內容過濾再到電商網商推薦，在相機、智能手機等消費品中也越來越多見。機器學習系統被用來識別圖像中的物體、將語音轉為文本，根據用戶興趣自動匹配新聞、消息或產品，挑選相關搜索結果。這類被應用程序越來越多地采用的技術，叫做深度學習。

　　傳統機器學習技術在處理原始輸入的自然數據方面能力有限。幾十年來，建構模式識別或機器學習系統需要利用嚴謹的工程學和相當豐富的專業知識設計出一個特征提取器，它能將原始數據(例如圖像像素值)轉化成適于內部描述或表征的向量( vector )，在提取器中，學習子系統(通常是一個分類器)可以檢測或分類輸入模式。

　　表征學習(representation learning)是這樣一套學習方法：輸入原始數據后，機器能夠自動發現檢測或分類所需的表征信息。深度學習是一種多層描述的表征學習，通過組合簡單、非線性模塊來實現，每個模塊都會將最簡單的描述(從原始輸入開始)轉變成較高層、較為抽象的描述。通過積累足夠多的上述表征轉化，機器能學習非常復雜的函數。就分類任務來說，更高層的表征會放大輸入信號的特征，而這對區分和控制不相關變量非常關鍵。比如，圖片最初以像素值的方式出現，第一特征層級中，機器習得的特征主要是圖像中特定方位、位置邊沿之有無。第二特征層級中，主要是通過發現特定安排的邊緣來檢測圖案，此時機器并不考慮邊沿位置的微小變化。第三層中會將局部圖像與物體相應部分匹配，后續的層級將會通過把這些局部組合起來從而識別出整個物體。深度學習的關鍵之處在于：這些特征層級并非出自人類工程師之手;而是機器通過一個通用(general-purpose)學習程序，從大量數據中自學得出。

　　某些根深蒂固的問題困擾了人工智能從業者許多年，以至于人們最出色的嘗試都無功而返。而深度學習的出現，讓這些問題的解決邁出了至關重要的步伐。深度學習善于在高維度的數據中摸索出錯綜復雜的結構，因此能應用在許多不同的領域，比如科學、商業和政府。此外，除了圖像識別和語音識別，它還在許多方面擊敗了其他機器學習技術，比如預測潛在藥物分子的活性、分析粒子加速器的數據、重構大腦回路、預測非編碼DNA的突變對基因表達和疾病有何影響等。也許，最讓人驚訝的是，在自然語言理解方面，特別是話題分類、情感分析、問答系統和語言翻譯等不同的任務上，深度學習都展現出了無限光明的前景。

　　在不久的將來，我們認為深度學習將取得更多成就，因為它只需要極少的人工參與，所以它能輕而易舉地從計算能力提升和數據量增長中獲得裨益。目前正在開發的用于深層神經網絡的新型學習算法和體系結構必將加速這一進程。

　　監督式學習

　　不管深度與否，機器學習最普遍的形式都是監督式學習(supervised learning)。比如說，我們想構造一個系統，它能根據特定元素對圖片進行分類，例如包含一棟房子、一輛車、一個人或一只寵物。首先，我們要收集大量包含有房子、車、人或寵物的圖片，組成一個數據集(data set)，每張圖片都標記有它的類別。在訓練時，每當我們向機器展示一張圖片，機器就會輸出一個相應類別的向量。我們希望的結果是：指定類別的分數最高，高于其他所有類別。然而，如果不經過訓練，這將是不可能完成的任務。為此，我們通過一個目標函數來計算實際輸出與期望輸出之間的誤差或距離。接下來，為了減小誤差，機器會對其內部可調參數進行調整。這些可調參數常被稱為「權重」(weight)，是實數，可看做定義機器輸入-輸出功能的「門把手」。在一個典型的深度學習系統中，可能存在著成千上億的可調權重及用以訓練機器的標記樣本。

　　為了正確地調整權重矢量( weight vector)，學習算法會計算出一個梯度矢量( gradient vector)。對每一個權重，這個梯度矢量都能指示出，當權重略微增減一點點時，誤差會隨之增減多少量。接著，權重矢量就會往梯度矢量的反方向進行調整。

　　從所有訓練范例之上，平均看來，目標函數( objective function)可被視為一片崎嶇的山地，坐落于由權重組成的高維空間。梯度矢量為負值的地方，意味著山地中最陡峭的下坡方向，一路接近最小值。這個最小值，也就是平均輸出誤差最小之處。

　　在實踐中，大多數業內人士都是用一種被稱為「隨機梯度下降」(SGD - Stochastic Gradient Descent)的算法(梯度下降Grident Descent 是「最小化風險函數」以及「損失函數」的一種常用方法，「隨機梯度下降」是此類下的一種通過迭代求解的思路——譯者注)。每一次迭代包括以下幾個步驟：獲取一些樣本的輸入矢量( input vector)，計算輸出結果和誤差，計算這些樣本的平均梯度，根據平均梯度調整相應權重。這個過程在各個從整個訓練集中抽取的小子集之上重復，直到目標函數的平均值停止下降。它被稱做隨機(Stochastic)是因為每個樣本組都會給出一個對于整個訓練集( training set)的平均梯度(average gradient)的噪音估值(noisy estimate)。較于更加精確的組合優化技術，這個簡單的方法通常可以神奇地快速地找出一個權重適當的樣本子集。訓練過后，系統的性能將在另外一組不同樣本(即測試集)上進行驗證，以期測試機器的泛化能力( generalization ability) ——面對訓練中從未遇過的新輸入，機器能夠給出合理答案。

　　很多當今機器學習的實際應用都在人工設定的特征上使用「線性分類」(linear classifiers)。一個「二元線性分類器」(two-class linear classifier)可以計算出特征向量的「加權和」(weighted sum)。如果「加權和」高于閾值，該輸入樣本就被歸類于某個特定的類別。

　　二十世紀六十年代以來，我們就知道線性分類只能將輸入樣本劃分到非常簡單的區域中，即被超平面切分的半空間。但是，對于類似圖像及語音識別等問題，要求「輸入-輸出函數」(input–output function)必須對輸入樣本的無關變化不敏感，比如，圖片中物體的位置，方向或者物體上的裝飾圖案，又比如，聲音的音調或者口音;與此同時「輸入-輸出函數」又需要對某些細微差異特別敏感(比如，一匹白色的狼和一種長得很像狼的被稱作薩摩耶的狗)。兩只薩摩耶在不同的環境里擺著不同姿勢的照片從像素級別來說很可能會非常地不一樣，然而在類似背景下擺著同樣姿勢的一只薩摩耶和一只狼的照片在像素級別來說很可能會非常相像。一個「線性分類器」(linear classifier)，或者其他基于原始像素操作的「淺層(shallow)」分類操作是無論如何也無法將后者中的兩只區分開，也無法將前者中的兩只分到同樣的類別里的。這也就是為什么「淺層」「分類器(classifiers)」需要一個可以出色地解決「選擇性-恒常性困境」( selectivity–invariance dilemma)的「特征提取器」(feature extractor)—— 提取出對于辨別圖片內容有意義的信息，同時忽略不相關的信息，比如，動物的姿勢。我們可以用一些常規的非線性特征來增強「分類器」(classifiers)的效果，比如「核方法」(kernel methods)，但是，這些常規特征，比如「高斯核」(Gaussian Kernel)所找出來的那些，很難泛化( generalize )到與訓練集差別別較大的輸入上。傳統的方法是人工設計好的「特征提取器」，這需要相當的工程技巧和問題領域的專業知識。但是，如果好的「特征提取器」可以通過「通用學習程序(General-Purpose learning procedure)」完成自學習，那么這些麻煩事兒就可以被避免了。這就是深度學習的重要優勢。

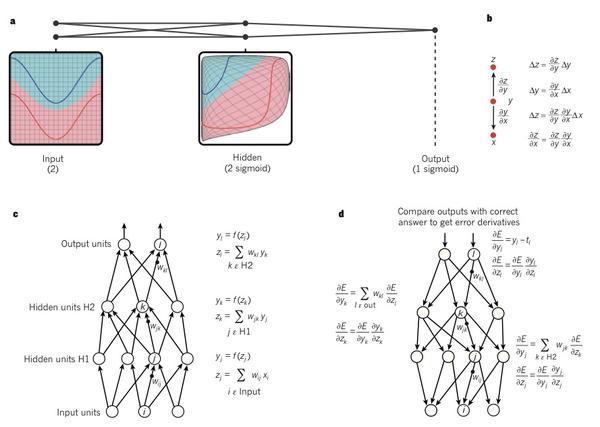
　　圖1| 多層神經網路和反向傳播

　　a. 一個多層神經網絡(如圖所示相互連接的點)能夠整合(distort)輸入空間(圖中以紅線與藍線為例)讓數據變得線性可分。注意輸入空間的規則網格(左側)如何轉被隱藏單元(中間)轉換的。例子只有兩個輸入單元、兩個隱藏單元和一個輸出單元，但事實上，用于對象識別和自然語言處理的網絡通常包含了數十或成千上萬個單元。(本節引用改寫自 C. Olah (http://colah.github.io/).)

　　b. 導數的鏈式法則告訴我們，兩個微小增量(即x關于y的增量，以及y關于z的增量)是如何構成的。x的增量Δx導致了y的增量Δy，這是通過乘以?y/?x來實現的(即偏導數的定義)。同樣，Δy的變化也會引起Δz的變化。用一個方程代替另一個方程引出了導數的鏈式法則( the chain rule of derivatives)，即增量Δx如何通過與?y/?x及 ?z/?x相乘使得z也發生增量Δz。當x,y 和 z都是向量時這一規律也同樣適用(使用雅克比矩陣)。

　　c. 這個公式用于計算在包含著兩個隱層和一個輸出層的神經網絡中的前向傳輸，每個層面的逆向傳遞梯度都構成了一個模組。在每一層，我們首先計算面向每個單元的總輸入值z，即上一層的輸出單元的加權和;然后，通過將一個非線性函數f(.)應用于z來得出這個單元的輸出。為了簡化流程，我們忽略掉一些閾值項(bias terms)。在神經網絡中使用的非線性函數包含了近些年較為常用的校正線性單元(ReLU) f(z) = max(0,z)，以及更傳統的 sigmoid函數，比如，雙曲線正切函數, f(z) = (exp(z) ? exp(?z))/(exp(z) + exp(?z)) 和 邏輯函數f(z) = 1/(1 + exp(?z)).

　　d. 該公式用于計算反向傳遞。在每一個隱藏層中，我們都會計算每個單元輸出的導數誤差，即上述層中上一層所有單元輸入的導數誤差的加權總和。 然后，將關于輸出的導數誤差乘以函數f(z)的梯度(gradient)，得到關于輸入的導數誤差。 在輸出層中，通過對成本函數進行微分計算，求得關于輸出單元的誤差導數。因此我們得出結論 yl - tl 如果對應于單元l的成本函數是 0.5(yl - tl) 2 (注意tl是目標值)。一旦?E/?zk已知，那么，就能通過yj ?E/?zk調整單元j的內星權向量wjk。

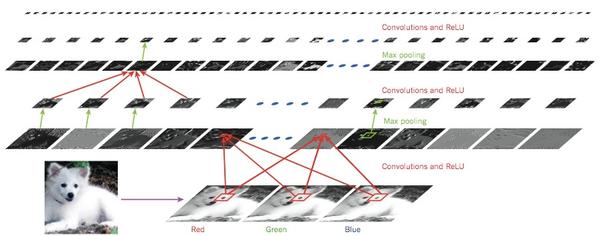
　　圖2 | 卷積網絡的內部