PID算法的FPGA實現

1.引言

在許多現代化的工業生產如冶金、電力等，實現對溫度的精度控制至關重要的，不僅直接影響著產品的質量，而且還關系到生產安全、能源節約等一系列重大經濟指標。

PID控制由于其魯棒性好，可靠性高，在常規的溫度控制中應用非常廣泛。目前工程的實際應用中，大多數模糊PID控制器都利用單片機軟件編程來實現，然而單片機的指令是按順序執行的，實時性不強，加上軟件實現容易受外界的干擾，抗干擾性能力差，對于實時性要求很高和外界干擾比較嚴重的系統不太適宜。本文選取FPGA(現場可編程門陣列)作為系統的主控制芯片，FPGA所有的信號都是時鐘驅動的，對于程序的執行具有并行運算的能力，顯著的提高了系統控制的實時性，在FPGA內部硬件實現還可以防止像單片機程序一樣，在惡劣的環境條件下發生程序跑飛的問題。尤其是現在FPGA器件有越來越多的參考設計方案以及IP(知識產權)核心庫方面的支持。利用FPGA設計的PID控制器一方面可以將實現PID算法的模塊單獨作為控制模塊來使用，直接去實現對控制對象的調節，另一方面，基于FPGA的PID控制算法也可以將其作為系統內的IP核，以便在多路或復雜的系統上直接調用，加快研發設計速度。

2.PID算法分析

2.1 離散PID算法

PID控制系統是一個簡單的閉環系統，如圖1所示，PID系統框圖中，整個系統主要包括比較器、PID控制器和控制對象，其中PID包括三個環節，即比例、積分和微分。

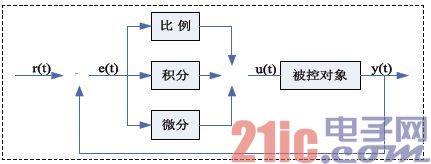
圖1 PID系統框圖

圖1中的r(t)作為系統的給定值，y(t)作為系統的輸出值，e(t)是給定值與輸出值的偏差，所以系統的偏差可以求得：

e(t)=r(t)-y(t) (1)

u(t)作為控制系統中的中間便量，既是偏差e(t)通過PID控制算法處理后的輸出量，又是被控對象的輸入量，因此模擬PID控制器的控制規律為：

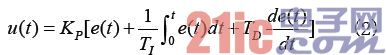
其中，KP為模擬控制器的比例增益，TI為模擬控制器的積分時間常數，TD為模擬控制器的微分時間常數。

2.2 離散PID算法

為了用微處理器實現PID算法，我們需要將模擬PID離散化，根據采樣時刻的偏差來實現PID算法，因此式(3.2)中的微分和積分項兩項內容作離散化處理。

假設T為采樣周期，則積分項可作如下變換：

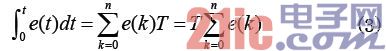
采樣周期的時間非常短，故微分可以近似的表示為：

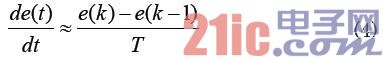
將式(3)和式(4)帶入式(2)后，可得到離散PID算法為(限于篇幅，推導過程省略)：

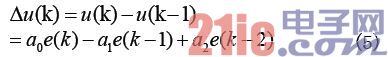
這個等式被叫做增量式PID控制算法。其中，乘積因子由PID控制參數KP、KI、KD確定：

3.PID算法的FPGA實現

由公式(5)知，增量式PID控制算法的具體實現步驟為：先通過誤差計算模塊求出偏差值e(k)、e(k-1)、e(k-2)，再通過乘積模塊求出三個信號分別與乘積因子的相乘，最后對乘積項求和得到最后的控制量。圖2所示為增量式PID算法結構圖。

3.1 誤差計算模塊

誤差計算模塊的目的是為了求出三次相鄰的偏差采樣值，即公式(3.8)中提到的e(k)、e(k-1)、e(k-2)，輸入的給定值r(t)與實際輸出值y(t)相減得到誤差值。Verilog HDL程序代碼如下，其中，ek0、ek1、ek2、rt、yt分別對應偏差值e(k)、e(k-1)、e(k-2)、r(t)、y(t)。

將上述程序在Quartus II軟件環境里完成編譯后，其仿真結果如圖3所示。

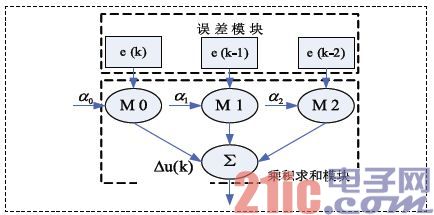
圖2 增量式PID算法結構圖

圖3 誤差模塊仿真圖

3.2 乘積和求和模塊

通過誤差計算模塊求出e(k)、e(k-1)、e(k-2)后，由公式(5)知，要計算出控制量還必須將其分別與乘積因子做乘法運算，通過硬件描述語言來實現乘法運算的功能：

按照上述程序，在Quartus II完成編譯后，其仿真結果如圖4所示。

圖4 乘法器仿真圖

現在可計算出α0e(k)、α1e(k-1)、α2e(k-2)三個乘積項的計算結果，將上面三個乘積項求和就可以得出控制量△u(k)。程序代碼如下所示，其中輸入val0[15..0]、val1[15..0]、val2[15..0] 分別對應α0e(k)、α1e(k-1) 、α2e(k-2)乘積的結果，輸出val[15..0]就是控制量△u(k)的值。

按照上述程序，在Quartus II完成編譯后，其仿真結果如圖5所示。

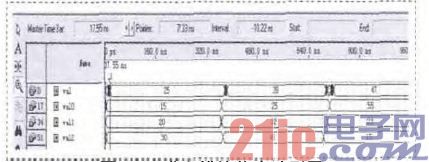
圖5 PID求和模塊仿真波形圖

3.3 溫度檢測及輸出控制電路設計

本文用到的溫度測量器件是K型熱電偶，溫度測量范圍為0～1200℃。熱電偶輸出的是模擬電壓信號，必須進行A/D轉換，同時還需對熱電偶進行冷端補償和非線形校正。為了解決上面的問題，本文采用的是K型熱電偶專用數字轉換器MAX6675芯片，MAX6675芯片內部集成了熱電偶放大器，內置高達12位的模數轉換器。還包括了非線性矯正、冷端補償、斷線檢測等功能模塊。MAX6675的工作溫度范圍為-20～85℃，溫度的測量范圍為0～1024℃，溫度分辨率可以達到0.25℃。假設D為A/D轉換后得到的數字量對應的十進制數值，那么測量溫度值T可以通過如下公式算出：

輸出控制電路采用的是PWM(脈寬調制)方式，實現對電阻爐的溫度控制。光耦芯片選用MOC3061，用于對強弱電路的隔離，雙向導通可控硅選用的是BT137_600E。如果占空比越高，那么相對可控硅導通的時間也就越長，電阻爐加熱溫度也就越高，反之溫度也就會慢慢散熱降低，從而達到控制爐溫的目的。

4.結語

本文分析了PID算法，給出了在FPGA內部硬件實現增量式PID控制的主要設計思路。在電阻爐為控制對象的溫控系統中，系統工作穩定，在整個過程沒有出現震蕩和較大波動，并且溫度控制精度在始終保持在5%以內;系統的抗干擾能力增強，對現場的各種噪聲和干擾具有較好的抑制作用。