基于換能器解卷積的高精度超聲波測距系統

超聲測距系統由于具有不受光線煙霧影響、抗電磁干擾能力強、距離信息直觀、成本低、使用方便等特點，廣泛應用于液位物位測量、位置角度跟蹤、移動機器人定位等場合[1，2]。為了進一步用于需要高的測距、定位精度的場合，國內外提出了多種高精度超聲波測距處理方法[3～6]。這些處理方法更多地針對接受到的超聲信號，沒有考慮到超聲換能器對測距精度的影響。在“移動機器人超聲導航傳感器”[7]和863項目“超聲地形障礙檢出傳感系統”中高精度超聲波測距研究的基礎上，本文從考慮超聲波換能器對測距精度的影響出發，研究了基于換能器解卷積的超聲波測距處理方法。

1 超聲波換能器對測距精度的影響

考慮發射—接收工作模式的超聲測距系統，以x(t)為發射信號，接收端得到的超聲信號為:

其中:hTR、hRV分別為發射、接收換能器的沖激響應，hair為傳輸空氣介質的沖激響應。超聲測距系統信號流程如圖1所示。

Cramer-Rao下界是時延估計(TDE)能達到的最小誤差，也即時延估計系統能達到的理論上的最佳精度。根據Cramer-Rao下界，假定信號和噪聲是不相關的平穩隨機過程，且信噪比SNR>>1，時延估計方差的Cramer-Rao下界為[8]:

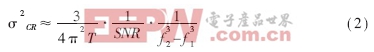
其中T為觀測窗，f1、f2分別為信號帶寬的上下界。

由上述公式可知，對時延估計系統來說，信號的帶寬越寬、信噪比越高、觀測時間越長，系統可達到的時延估計精度越高。在信噪比和觀測時間一定的條件下，信號帶寬決定了時延估計的精度。

由式(1)，超聲測距系統接受信號的帶寬取決于發射信號、發射接收換能器和空氣介質，對于通常的超聲測距系統，超聲波換能器對信號帶寬起主要作用。因為寬帶發射信號可以容易地產生，空氣介質的傳遞函數也是寬帶的，而通常的氣介超聲波換能器為了平衡發射效率、接收靈敏度，其帶寬較窄，如常用的T/R40—16型超聲換能器，中心頻率40kHz，3dB帶寬時頻率約為3.8kHz。這樣，影響超聲測距精度的主要是換能器的窄帶頻率特性。

2 基于換能器解卷積的超聲測距處理方法

為了抵消換能器窄帶特性對接受信號的影響，可以采取解卷積的處理方法，即構造一個沖激響應為hdecon的濾波器，對換能器沖激響應進行解卷積，使其與發射、接受換能器的聯合頻率響應是一個寬帶響應，從而輸出寬帶超聲信號，提高測距精度。

自適應濾波器可自動調節本身的沖激響應特性，即用自適應算法調整濾波器的數字系數，然后按某種準則來判斷誤差信號是否最小，從而達到最優化濾波。因此，可以把經發射、接收換能器(不經過空氣介質傳輸)的實際超聲信號輸入自適應濾波器，用要求的理想寬帶信號作為自適應濾波器的訓練信號構造濾波器。自適應算法收斂后即得到了解卷積所需的濾波器。

用自適應濾波器法構成解卷積濾波器構造的原理圖如圖2所示。濾波器采用橫向FIR型，LMS(最小均方誤差)算法。

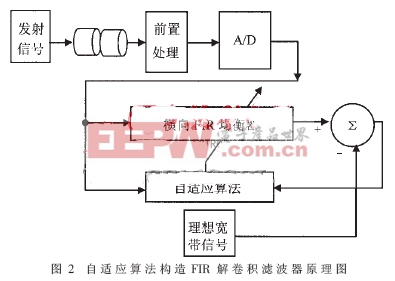
3 LMS自適應算法介紹

設輸入信號為X(k)，目標信號為Y(k)，濾波器輸出信號為 Y′(k)，則輸出信號與目標信號的誤差為:

而J顯然是濾波器沖激響應h(k)的函數，因此濾波的問題在數學上就是尋求使J最小的h(k)。LMS算法是常見的自適應算法。它是一種遞推運算，不需要對信號的統計特性有先驗的了解，而只是使用瞬時估計值根據遞推得到最優解。運算得到的只是FIR濾波器權重系數的估計值，隨時間的發展，權重系數逐步調整，估計值逐步改善，最終達到收斂。LMS算法中，權重按下式逐步更新:

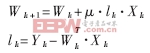
其中:Wk為第k個采樣點的權重系數，ek為第k個采樣點的誤差，Yk為理想輸出信號，μ為控制穩定性和收斂速度的系數。μ大則收斂快，但太大，算法將變得不穩定。一般按下式取值:

式中:N為FIR濾波器的長度;Px為輸入信號功率，按下式計算(M為輸入構造理想換能器的脈沖響應序列長度):

4 實驗結果

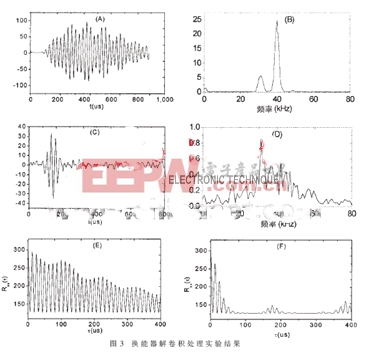
實驗設置為:發射信號x(t)為脈寬12.5μs的單脈沖;發射、接收換能器為T/R40—16;ADC為MAX153，速率1Msps，8bit;FIR濾波器權系數長度為80;以發射信號x(t)通過中心頻率40kHz，帶寬20kHz理想濾波器的輸出信號作為構造解卷積濾波器的訓練信號。

從圖3的實驗結果可以看出，與未經解卷積處理的接收信號比較(時域波形圖3A，頻率域圖3B)，采用構造好的濾波器對換能器特性進行解卷積后得到的接收超聲信號(圖3C)帶寬明顯變寬(圖3D)，信號的相關峰明顯尖銳化(處理前圖3E，處理后圖3F)，最大相關偽峰衰減從-0.346dB顯著提升為-1.278dB，提高了信號檢測精度。圖4所示為采用換能器解卷積處理后的超聲相關法測距的精度情況，可以看到系統測距精度有了明顯的提高，10m內測距精度達6.6mm[9]。

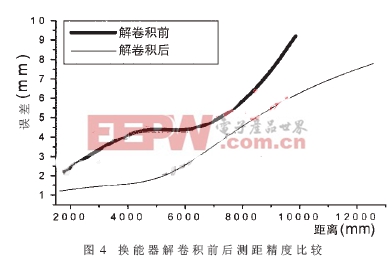
為了提高超聲波測距系統的測距精度，通過自適應算法構造用于抵消換能器窄帶特性的解卷積濾波器，采用換能器解卷積的測距精度比原始的測距精度有明顯的提高。這種換能器解卷積處理方法同樣可適用于其他類似的傳感系統。