隨機共振方法在弱信號檢測中的應用

在非線性系統、信號和噪聲共同產生協同效應中，非線性系統呈現的方式是系統的勢壘。勢壘越高，意味著產生協同效應時要求信號和噪聲的能量越大。反之，要求信號和噪聲的能量就越小。從方程知道，變化的a和b都能控制系統勢壘值。為了方便起見，現在令b=1。圖3是系統在b=1的情況下，系統勢壘值與a之間的關系曲線圖。

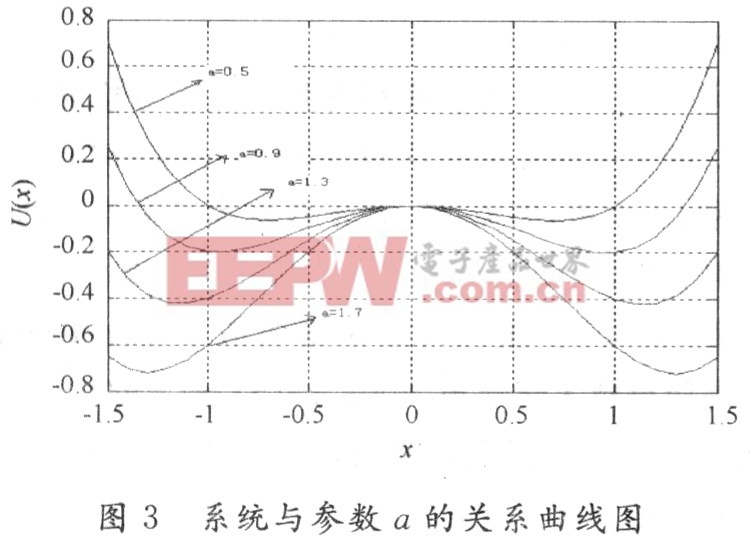
從圖3中可以看出，隨著a值的變小，系統的兩個勢阱的距離拉近，同時系統的勢壘降低。這樣系統的阻尼力減小，使系統進入隨機共振狀態時所需的能量降低，從而有利于系統更好地提取有用信號特征。然后研究a=1時，系統勢壘值與b之間的關系曲線圖。
圖4是系統在a=1時，不同b值的系統勢函數曲線圖。從圖中可以看出，隨著b值的變大，系統的兩個勢阱的距離拉近，同時系統的勢壘降低。這樣系統的阻尼力減小，使系統進入隨機共振狀態時所需的能量降低，從而有利于系統更好地提取有用信號特征。

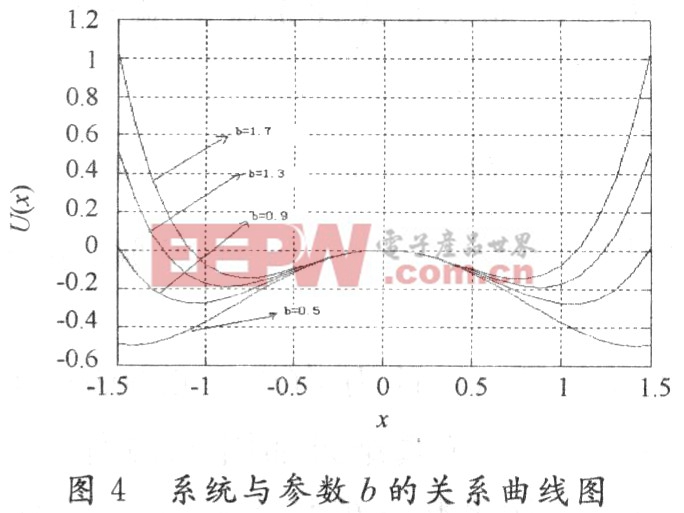
另外，對輸出響應x(t)進行分析，在初始條件x0=x(t0)下，若t0→-∞，則初始條件的影響會消失而不用考慮，于是x(t)的均值將變成為一個周期函數：

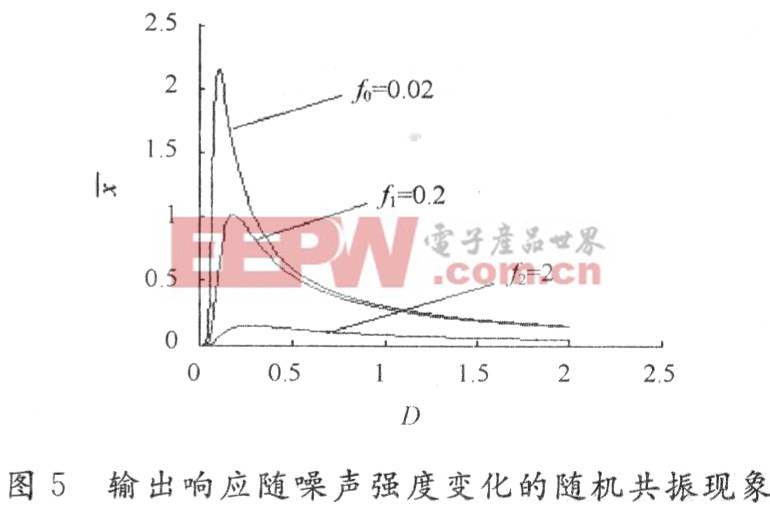
其中，rk是克萊默斯(Kranmers)逃逸速率；E[x2]是靜態系統(A=0)依賴與噪聲強度D的方差，在兩態情況下有近似關系E[x2]=x2m。由式可知，幅值x取決于噪聲強度D，即系統的響應受噪聲強度的控制，它首先隨D的增大而到達一個極大值，然后再減小，這就是著名的隨機共振現象，如圖5所示。