基于WLS-KF的GPS非線性動態濾波研究
1.2 KF算法
KF算法對一個離散時間線性系統的狀態進行最優估計,使系統狀態的估計值有最小均方誤差(MMSE)。
考慮一個多輸入多輸出的離散時間線性動態系統,其狀態方程可表示為:

向量wk和vk分別表示狀態噪聲和測量噪聲,假設它們都是均值為零的正態白噪聲且相互獨立,即:
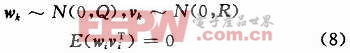
KF算法通過如下的時間更新過程和測量更新過程來對系統狀態進行估計。

計算完測量更新方程后,整個過程再次重復,上一次計算得到的后驗估計被作為下一次計算的先驗估計。
1.3 WLS-KF算法
1.3.1 基本思想
算法基本思想是通過WLS方法計算隨機變量經過非線性變換后的分布參數,它利用離散個加權點來確定近似直線。
設待確定的近似線性化模型為:

式中:(xn,f(xn))表示設置的離散加權點;p(xn)表示其對應的權系數,n=1,2,…,n。
濾波器相關文章:濾波器原理
濾波器相關文章:濾波器原理
電源濾波器相關文章:電源濾波器原理









評論