一種基于人工神經元實時諧波電流數字檢測方法

摘 要： 本文基于人工神經網絡理論，提出了人工神經元自適應諧波和無功電流、諧波電流數字檢測新方法，實驗結果證明了所提出的方法的正確性及實時性。

關鍵字： 諧波 無功電流 數字檢測方法 實時實現

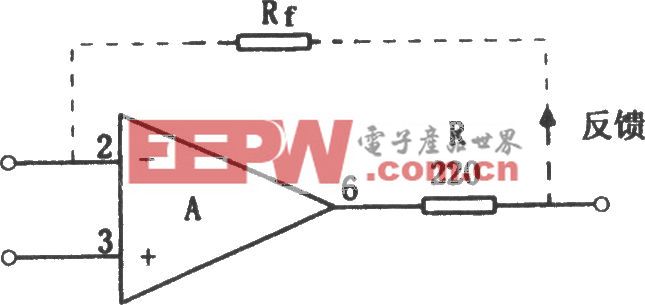
諧波對電網和用電設備的有很大的危害[1、2]，由諧波污染引起的問題很嚴重,必須進行合理地治理。裝設補償裝置,進行諧波和無功功率的補償，采用濾波器對畸變電流進行濾波和補償是解決電網諧波和無功干擾的重要手段，也是消除諧波電流對電網影響的最終措施。有源電力濾波器原理圖如圖1.1所示,有源濾波器向電網注入與負載諧波電流幅值相等的反相諧波電流ic以抵消原有諧波電流，使電源電流is近似為正弦波。諧波檢測電路檢測的結果是控制電路的輸入，從而決定控制電路的輸出，而控制電路的輸出又決定了有源電力濾波器的輸出補償電流ic,所以有源電力濾波器補償電流大小、方向、相位及精度很大程度取決于諧波的檢測電路。如果檢測電路具有實時性好、精度高、誤差小等優點，有源電力濾波器的補償就會較好。否則，有源電力濾波器補償電流ic要么大于諧波電流，出現過補償，從而成為又一諧波源；要么ic小于諧波電流，出現欠補償。諧波檢測對有源電力濾波器補償起很大的決定性作用，如果要求有源電力濾波器的補償效果好，必須使諧波檢測電路檢測電路具有實時性好、精度高、誤差小等優點，實時性和連續性均有賴于無功電流的檢測的實時性和精度，所以有必要深入研究諧波測量電路。

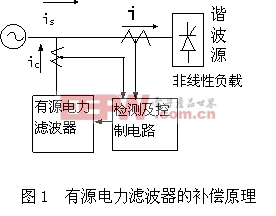
傳統的檢測方法有Fryze時域分解、槽形濾波器、基于頻域的FFT變換法、用于不平衡三相系統的同步檢測法，這些方法主要的缺點是1)時延較大；2)難以實現，如槽形濾波器法；3)當電壓畸變時將帶來較大的誤差。近來提出的P-Q法[3]的缺點是在電源畸變大時，含有畸變的電壓，使計算的iaf、ibf、icf也含有諧波，而、由各次諧波電流成分組成，因而該法在諧波較大的情況下誤差較大。

1 基于自適應干擾對消原理的諧波檢測方法

自適應干擾對消理論技術是近年來得到廣泛使用的信號處理技術［4、5、6］。由于它能夠通過不斷的自我學習和自我調整使系統處于最佳狀態，所以在不同的領域得到應用。

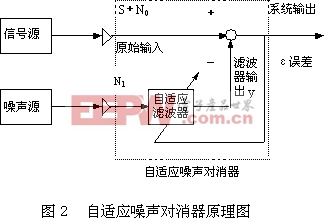
自適應干擾對消原理是：系統有兩個輸入端——原始輸入和參考輸入端（原理圖參見圖2）。系統的原始輸入是信號S和加性噪聲N0，S和N0不相關。系統的參考輸入端是噪聲N1與N0相關但與S不相關。N1經過自適應濾波器處理后與原始輸入信號相減，系統經過自適應算法的調整，使系統平均輸出功率最小，也就是使N1逼近N0，然后減去原始輸入中的N0成分，以達到抵消干擾的目的。可以證明：此時系統的輸出ε是信號S在最小均方準則下的最佳估計［7］。

諧波檢測的目的為了實時地提取畸變電流中的諧波和無功電流。如果把基波電壓作為參考輸入，而非線性負荷電流作為原始輸入。與上述情況相似，通過自適應濾波器出來后的參考輸入，最終被迫在幅度和相位上逼近電壓原始輸入中的基波信號，然后從負載電流中減去這基波分量，結果為系統的輸出—所有諧波分量和無功之和，就達到檢測諧波和無功的目的了。同理，將基波及與基波的正交函數作為輸入，就達到檢測諧波電流的目的了。

2 基于人工神經元自適應的諧波檢測方法

2.1 無時延的人工神經元諧波和無功檢測方法

單個人工神經元有一定的處理、計算及映射能力，具有自適應和自學習能力，所以上述的自適應濾波器實現的檢測系統，也可以用神經元代替，如果性能較好、學習算法簡單，由于神經元結構簡單，就能達到快速檢測諧波的目的。

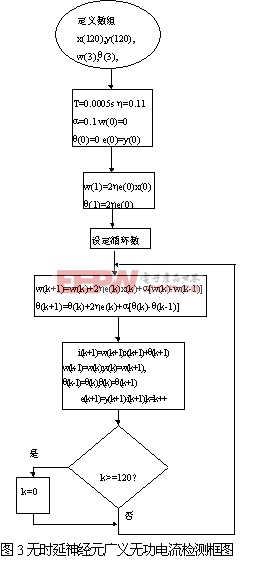
無時延的諧波檢測方法可以檢測廣義無功電流ib（也就是諧波電流ih及無功電流i1q之和）。無時延自適應神經元諧波及無功電流檢測方法的框圖見圖3。

2.2 正交函數輸入的神經元自適應諧波檢測方法

這種方法實際上是有時延的神經元諧波檢測方法的特例，也就是將時延設定為－T/4，將m設定為1，而形成兩個正交的函數作為參考輸入，在實現時把這種方法的時延設定為－T/4，它的實現可以取保存在內存的現在時刻以前四分之一周期的電壓采樣作為余弦函數。如果在電壓頻率較恒定的情況下（一般電壓畸變很小），可以先計算出采樣數目差，然后用現時刻的采樣電壓和保存在內存的現在時刻以前計算出的采樣電壓作為參考輸入，那么，參考輸入向量為：

X(k)=[u(k),u(k+T/4)] (1)

在電壓頻率變化不大，在這里只要根據采樣的頻率和基波平移900相角所需要時間來計算現時刻以前的時刻：

T/4¸T′=1/(50´4)¸(1/2000)=10 (2)

式中T為頻率固定的電壓的周期，T′為采樣周期。圖4為正交函數輸入的電壓頻率固定的神經元自適應諧波檢測方法的框圖。

2.3 基于人工神經元自適應的諧波檢測方法的實現

在這里，神經元為離散型輸入，這里權值w為模擬量，在區間[-1,1]之間取隨機值，采樣周期取2000HZ，初始閥值為零,學習率先選h＝0.11，以后再根據實驗結果進行調整，慣性系數為a＝0.1。

其中數組x(120)，y(120)分別為電壓、電流采樣后保存在PC機內存的數值。

3 實驗結果

本實驗將Pentium的CPU、主頻率為100MHz、內存為8MB的PC兼容機，作為數據計算的硬件，將PCL-818L多功能卡作為集數據采樣、A/D轉換、數據傳輸硬件。由于單位方波具有代表性，本文使用單位方波非線性負載電流做實驗。

3.1 無時延的人工神經元諧波和無功檢測方法實驗結果

3.1.1單位方波非線性負載電流的實驗結果

通過大量地實驗研究，發現對于不同的h值，計算的結果與實驗結果的誤差不同，當h＝0.04，a＝0.01時，ir趨近i1p，id逼近ic，誤差也很小，詳見圖5。圖5是初始權值為在－1到1的隨機值,初始閥值為零。利用電源電壓作為參考輸入，采樣頻率為2000Hz（下面實驗都為2000Hz）對幅值為1的方波非線性負載電流計算它的諧波及無功電流的實驗結果。為了了解及驗證實驗的結果，在圖中同時畫了ic（檢測值）和i1p（由理論計算得到的）的波形，圖5.b為從圖5.a中分

離出來的有功電流，諧波及無功電流的波形示于圖5.c中，圖5.d為檢測出的諧波及無功電流與理論值之間的誤差。由圖5可以明顯地看出在第一個周期內無論是有功電流還是諧波及無功電流都與理論值有一定的差別，大約在第二個周期它們的差別就不太大了，計算有功電流ir逼近其理論值i1p、而計算諧波及無功電流id趨近于理論廣義無功電流ic，它們的誤差在第二周期以后僅僅在0.1A以下，約占總電流的5％左右，從上述兩種結果可以看出，神經元的學習率h合理選擇對神經元的學習收斂具有較大的影響，合理的學習率h選擇可以加速收斂。

3.1.2 頻率變化的方波非線性負載電流的實驗結果

詳見圖6。該結果是在h＝0.04，a＝0.01條件下，從新啟動系統，在第三個周期改變負載電流的頻率，從50Hz變為55Hz。從圖6.b、6.c及6.d中可以清楚地看出:頻率對無延遲神經元諧波檢測系統來說影響不大，也就是說，該方法對頻率的變化有較強的適應性，能夠幾乎完全跟隨頻率的變化，有功電流、諧波及無功電流都能隨著頻率的變化而變化，誤差率沒有因為頻率改變而變化。

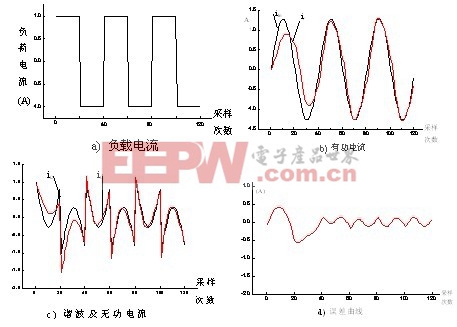
圖5 h＝0.04時無時延諧波檢測實驗結果

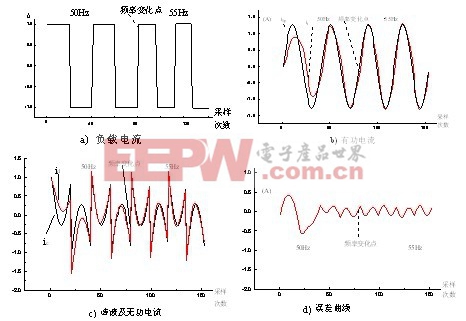
圖6頻率變化時無時延諧波檢測結果

3.2正交函數輸入的神經元自適應諧波檢測方法

3.2.2 負載電流變化的方波檢測結果

結果詳見圖7。從圖7.b和圖7.c中可以看出，當負載電流從1A突變到0.5A時，大約經過一個周期的適應，計算基波電流ir和諧波電流id逼近它們的理論值i1、ih，說明這種方法對負載電流變化的跟隨性也比較好。從誤差曲線圖7.d看，在負載電流變化的第二周期，誤差就小于0.1A了。

3.2.3 頻率變化的方波非線性負載電流檢測結果

從圖8中可以清楚地看出，正交函數作為參考輸入的神經元自適應諧波檢測系統對頻率變化不“敏感”，在頻率變化時，不會產生突變，能夠迅速跟隨頻率變化，在圖8.b、8.c中計算基波電流ir和諧波電流id與緊密地隨著它們的理論電流i1、ic變化而變化。因此，系統始終具有對被檢測的負載電流頻率自動跟隨能力。

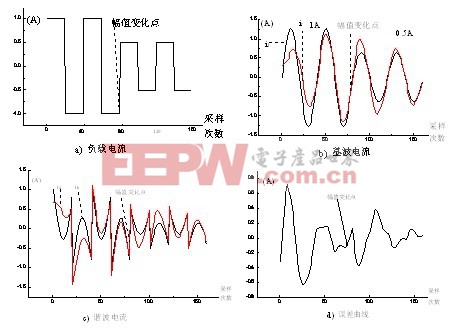
圖7 方波非線性負載變化時檢測結果

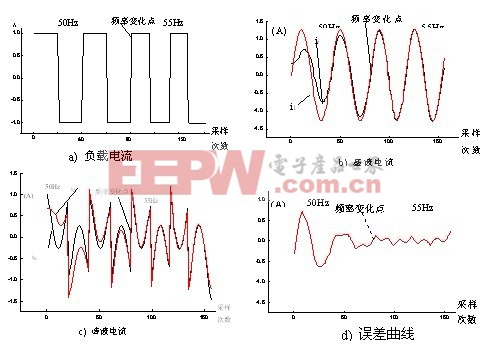
圖8 頻率變化方波負載電流檢測結果

4 結論

綜上所述，實驗結果證明了所提出的無時延的神經元自適應諧波和無功電流檢測方法以及正交輸入神經元自適應諧波電流檢測方法的正確性，所提出的方法對負載電流的頻率變化及幅值變化具有自適應性，證明了所提出的方法具有良好的實時性。從而本文所提出的方法確實可行。

參考文獻：

[1] Joseph S.Subjak et al., Harmonics-causes, effects, measurements, and analysis; An Update, IEEE Trans. on Ind. April, VOL.26, NO.6, 1034-1042, Nov./Dec. 1990

[2] D.V.Bose, Harmonics analysis and suppression for electrical system supplying static converter and other nonlinear loads, IEEE Trans. on Ind. April, vol.15, NO.5, 1979

[3] 湯紅誠 張曉清馮璞喬，諧波及無功電流實時檢測方法的現狀和展望，后勤工程學院學報，VOL.14,NO.3,48-53,1998

[4] 羅世國，有源電力濾波器的研究，博士學位論文，重慶大學， 1～2，1993

[5] John R. Glover, Adaptive Noise Canceling Applied to Sinusoidal Interference, IEEE Trans. on Accost, Speech, and Signal Processing,Vol.ASSP-25, 484-491,Dec.1977

[6] C.F.N. Cowan and P.M. Grant, Adaptive Filters, Prentice-Hall, Inc., 1985

[7] 湯紅誠，諧波電流數字檢測方法的研究及實現，碩士學位論文，后勤工程學院，18-20，1999