一種改進的小波閾值信號去噪方法

摘要 為改進濾波效果，提高去噪質量。通過分析軟硬閾值去噪的原理和方法，為小波闞值信號處理提出了一種改進的去噪方法。該方法綜合了軟硬閾值的特點，對其參數進行優化設計，通過調節參數值以更好地獲得閾值估計。針對改進后的去噪算法，通過Matlab仿真比較了傳統的小波軟硬閾值算法與該算法的消噪效果，結果表明，提出的方法有更好的消噪效果和穩定性。
關鍵詞 小波閾值去噪；閾值函數；信噪比；均方誤差

小波變換與傅里葉變換、窗口傅里葉變換相比，它是一個時間和頻率的局部變換，因而能有效地從信號中提取信息，通過伸縮和平移等運算功能對函數或信號進行多尺度細化分析，解決了傅里葉變換不能解決的許多問題。
小波變換被譽為“數學顯微鏡”，是調和分析發展史上里程碑式的進展。小波理論被認為是對傅里葉分析的重大突破，是近年來信號處理領域的研究熱點，許多學者將小波在理論上的研究成果應用到諸如圖像壓縮、特征提取、信號濾波和數據融合等方面。小波之所以在信號處理領域具有很大的優勢，在于小波變換可以獲得信號的多分辨率描述，同時，小波變換具有豐富的小波基可適應不同特征的信號。隨著小波理論的發展，Mallat提出了模極大值重構濾波，Xu提出了空域相關濾波和Donoho提出了小波域閾值濾波來消除噪聲。一般地，不同性質的噪聲需要采用不同的消噪方法處理。
上述算法都存在參數的選取問題，不同的參數選取對濾波的效果會有一些差異。Donoho的傳統小波閾值去噪方法的實現最簡單、計算量最小。但其在理論上找到的最優通用閾值，實際應用中效果并不理想。因此，文中在Donoho的傳統小波閾值去噪方法的基礎上，改變了小波閾值函數的部分參數得到了一種新的小波閾值函數，既避免了硬閾值函數的不連續性，又可以自適應去噪，從而有效地保存了信號的邊緣信息。仿真結果表明，改進后方法有更好的去噪性能。

1 小波閾值的去噪原理
小波變換具有一種“集中”的能力。信號經小波變換后，可以認為由信號產生的小波系數包括有信號的重要信息，其幅值較大，但數目較小，而噪聲對應的小波系數幅值小。通過在不同尺度上選取一合適的閾值，并將小于該閾值的小波系數置零，而保留大于閾值的小波系數，從而使信號中的噪聲得到有效的抑制，最后進行小波逆變換，得到濾波后的重構信號。
小波去噪的基本思路如圖1所示。信號先經過預處理，然后利用小波變換講信號分解到多尺度上，再對每一層小波系數進行閾值處理，最后對處理后的小波系數進行信號重構。

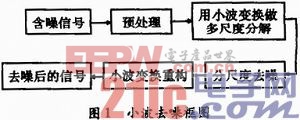
設一個含噪聲的一維信號模型可以表示為f(i)=s(i)+n(i)，其中s(i)為原始信號，n(i)為方差σ2的高斯白噪聲，服從N(0，σ2)。
1．1 小波硬閾值去噪的步驟
(1)對信號求小波變換。
(2)除了最粗尺度信號外，將各細節信號作閾值處理，閾值t取為，當某位置小波變換值大于閾值時，保留原值，否則置零，用公式表示為

(3)利用小波變換重構，求出信號的濾波值。
1．2 小波軟閾值去噪的步驟
(1)對信號求小波變換。
(2)除了最粗尺度信號外，將各細節信號作閾值處理，閾值t取為，當某位置小波變換大于閾值時，向著減小系數幅值的方向作一個收縮t，否則置零，用公式表示為

其中，sgn(x)為符號函數。