利用Teledyne LeCroy示波器測量噪聲
參數統計結果包括了最小值和最大值。如果您想查看多次連續捕獲的參數值的變化過程,可以使用Trend函數。Trend按測量的次序從左到右依次畫出每次測量的參數值。圖8顯示的例子中F4是參數P1的趨勢圖,反應了通道1波形的標準偏差的變化趨勢。每捕獲一次會得到一個標準偏差值,F4顯示出按次序測量的逐次結果。Trend波形可以當作是任何其它波形一樣再進行測量和分析。

推導出來的測量參數
另外一個感興趣的噪聲參數是振幅因數,即波形的峰值和有效值的比值。振幅因數決定了信號中峰值變化的動態范圍。雖然示波器中沒有雙極性的“峰值”參數,我們可以通過通道1中的信號的絕對值“創造”一個這樣的參數值。將負值翻轉到波形的正區域,然后使用最大值參數得到每次捕獲的正向正大值和負向最大值中的極大值。請注意這種方法可以行得通是因為信號平均值為零。 我們可以利用參數數學運算來計算出振幅因數。參數數學運算的設置如圖9所示,我們計算出振幅因數結果為參數P4,是P3和P1的比值。測量結果如圖8所示,得到的結果平均值是3.6。圖8中F6顯示出參數P4的直方圖,其分布并不是高斯的,這是由絕對值和最大值的數學運算有關的非線性過程引起。
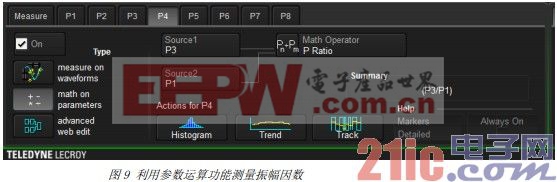
利用nbpw測量單點噪聲
另外一種對噪聲進行單點測量的方法是采用光領域的窄帶功率測量(Narrow-band power,nbpw)方法。nbpw通過計算某個頻率點的離散傅立葉變換來測量該頻點的功率。輸出單位是dBm。該方法對于測量噪聲并不是很非常方便,我們更喜歡使用線性單位 V^2 /Hz的噪聲功率譜密度來測量。幸運地是,Teledyne LeCroy示波器能夠嵌入算法來對參數進行更復雜的運算以得到需要的測量結果。這比圖9中振幅因數的簡單比例參數要復雜得多。這個測量結果如圖10所示。
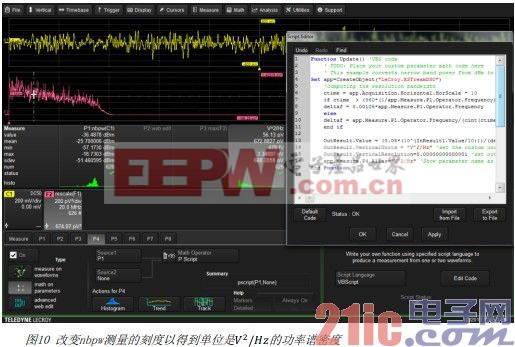
利用nbpw測量單點噪聲
另外一種對噪聲進行單點測量的方法是采用光領域的窄帶功率測量(Narrow-band power,nbpw)方法。nbpw通過計算某個頻率點的離散傅立葉變換來測量該頻點的功率。輸出單位是dBm。該方法對于測量噪聲并不是很非常方便,我們更喜歡使用線性單位 V^2 /Hz的噪聲功率譜密度來測量。幸運地是,Teledyne LeCroy示波器能夠嵌入算法來對參數進行更復雜的運算以得到需要的測量結果。這比圖9中振幅因數的簡單比例參數要復雜得多。這個測量結果如圖10所示。

圖12給出了本例中用于重新定標nbpw參數的VB代碼。

圖12 參數運算的VB代碼,將nbpw結果由dBm轉換為V^2/Hz
代碼算法分別將每個nbpw測量結果由對數轉換為線性的刻度(V^2),讀出捕獲的數據長度,然后計算出FFT的有效分辨帶寬。接下來,算法中利用這個值得到單位是V^2/Hz的功率譜密度。
偽隨機序列長度
如果您在研究的是偽隨機序列噪聲源,您可以輕松地使用Teledyne LeCroy示波器的光相關函數測量序列間隔。
圖13中利用了波形C1的自動相關函數表示這種測量的結果。自動相關函數產生的峰值點和偽隨機碼型的重復周期相對應。本例中,參數P7測量出碼型周期是131us。這和125MHz的時鐘頻率的16384個時鐘周期序列長度是一致的。
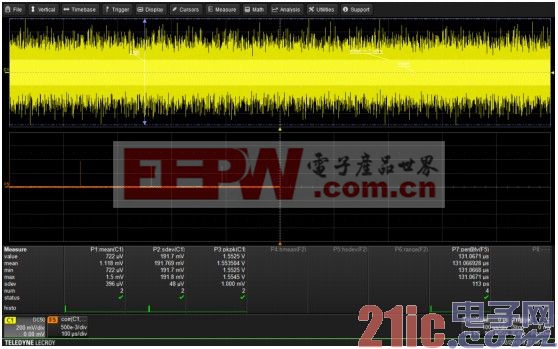
圖13 利用自動相關函數來確定偽隨機序列的長度
Teledyne LeCroy示波器擁有噪聲測量的時域,頻域,統計域的一切必要的工具,對于熟悉這種類型測量的工程師來說提供了很大的靈活強大的分析能力。











評論